二叉樹（4）紅黑樹_ZenDei技術網路在線

封裝基於 BinaryTreeOperations 的紅黑樹（一種自平衡的二叉查找樹）。除了提供 BinaryTreeOperations 中的部分基礎介面外，增加按鍵的插入和按鍵或節點指針的刪除操作。在閱讀本文前，您應該先瞭解二叉樹中的旋轉是怎麼回事（相關文章很多且簡單，筆者不再贅述）。 ...

封裝基於 BinaryTreeOperations 的紅黑樹（一種自平衡的二叉查找樹）。

除了提供 BinaryTreeOperations 中的部分基礎介面外，增加按鍵的插入和按鍵或節點指針的刪除操作。

在閱讀本文前，您應該先瞭解二叉樹中的旋轉是怎麼回事（相關文章很多且簡單，筆者不再贅述）。

講解紅黑樹的教程很多，但是很多講解並不足以讓讀者清楚的學會紅黑樹，尤其是刪除操作，許多教程十分凌亂，因此本文將使用清晰的層次分類及必要的圖進行講解。

節點定義：

enum class Color :bool { RED = 0, BLACK };
struct Node
{
    _Ty key;
    Node* left = nullptr;
    Node* right = nullptr;
    Node* parent = nullptr;
    Color color = Color::RED;
    Node(const _Ty& _key) :key(_key) {}
};

紅黑樹的規則：

　　① 每個節點是紅色或者黑色。

　　② 根節點是黑色。

　　③ 每個葉子節點是黑色（註意：這裡的葉子節點指為空的葉子節點）。

　　④ 如果一個節點是紅色，則它的孩子必須是黑色（或者說支路上不得出現連續的紅節點）。

　　⑤ 從任意節點到其葉子節點的所有路徑中，所辦含的黑色節點數相同（葉子節點同樣指為空的節點）。

請務必儘快熟練的記住以上規則（尤其是 ②，④，⑤），儘管這看似複雜，但在應用中正是因為這些特性會使得紅黑樹沒這麼難。

紅黑樹的增刪操作分為兩步：

　　① 按二叉查找樹的規則將節點插入到相關位置或刪除相關節點。

　　② 討論各種情況，若紅黑樹失衡則採取相關方法進行調整使之重新恢復平衡。

插入操作（令插入的節點為 cur，cur 的父節點為 par，par 的兄弟節點為 uncle，par 的父節點為 gpa）：

　　如嵌套 if else 一樣，我們將插入情況分為兩類（稱為外層分類），再根據這兩類的子情況進行其他分類（稱為內層分類）。

　　註意，新插入節點 cur 一定是紅色（因為這不會違背規則 ⑤，只有可能違背規則 ① ④，違背 ① 時容易處理，即插入空樹時只需將其變為黑色即可）。

　　　　為何寧願違背 ① ④ 而不寧願違只背 ⑤（即新插節點是黑色）？（你可以理解為這會更容易實現自平衡，不用過於糾結）。

　　　　插入空樹情況比較簡單，後文不特地說明該情況。

　　① 外層分類分為：par 是黑色或 par 是紅色。

　　② 內層分類是在 par 是紅色的情況下分類的，這在稍後進行講解。

　　現在先解決 ①：

　　　　1) par 是黑色時，直接插入即可（這不會打破平衡）。

　　　　2）par 是紅色（打破規則 ④），進入 ②。（註：此時 gpa 一定是黑色，看規則 ④）。

　　現在解決 ② （分為 uncle 是紅色或 uncle 是黑色）：

　　　　1）如圖 uncle 是紅色時（空的黑色節點沒有畫出）：

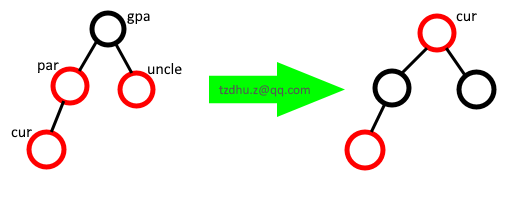
　　　　　　如圖進行變色後將 cur 指向 gpa 的節點，繼續執行 1）。

　　　　　　直到 cur 是紅色且為根節點時，直接將根節點變黑即可。或者出現新的 uncle 是黑色時進入後面的情況。

　　　　2）uncle 是黑色時分為四類情況（不用擔心，原理都一樣，分為兩類也可以的，這裡也可以類似 AVL 樹四種旋轉情況）該情況調整後便已經平衡，可直接返回。

　　　　　　① 直接看圖，圖中給出 par 是左孩子的兩種情況：

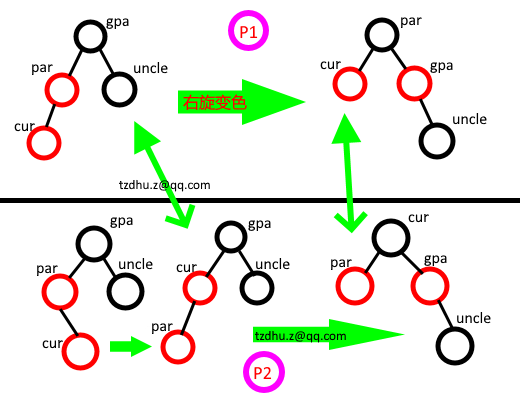
　　　　　　　　圖上P1，以 gpa 右旋（看！是不是類似 AVL 樹的左左_右旋！），並交換 par 和 gpa 的顏色（小的兩類情況是：cur 是左孩子還是右孩子）。

　　　　　　　　圖下P2，先將 gpa 的左孩子左旋，在將 gpa 右旋（看！是不是類似 AVL 樹的左右_左右旋！），然後交換 cur 和 gpa 的顏色。

　　　　　　② 接下來，par 是右孩子的兩種情況（小的兩類情況同樣看 cur 是左孩子還是右孩子）。

　　　　　　　　由於 ② 與 ① 是左右對稱的情況，因此交給讀者自行思考（用 AVL 樹的旋轉方法類似的話是：右右_左旋和右左_右左旋），不需要筆者繼續畫圖了吧！

至此，插入操作結束！總結......就不用了吧。接下去是刪除操作，情況很多，坐穩扶好！！！（不用慌，筆者會以清晰的層次進行分類說明）。

刪除操作（令待刪除節點為 cur，cur 的父親為 par，cur 的兄弟為 bro，bro 的左孩子為 LC，右孩子為 RC）：

在進行分類解決前，根據紅黑樹的規則，我們需要知道一些隱藏的特性，正如前文所說，正是因為這些隱藏特性，會使得紅黑樹變得稍微簡單。

以下以隱藏特性命名：

　　① 紅節點要麼沒有孩子，要麼有兩個孩子，不存在只有一個孩子的情況。

　　② 黑節點只有一個孩子時，該孩子一定是紅色，且該孩子無孩子。

　　說明：①：若紅節點只有一個孩子，孩子為紅則違背規則 ④，孩子為黑則違背規則 ⑤（無需圖也能理解吧）。

現在對刪除情況進行分類：

　　一、cur 是紅色。

　　二、cur 是黑色。

　　三、子情況是在 ② 的條件下分類的，這在稍後進行講解。

現在解決一（此時 cur 不可能是根，看規則 ①）：

　　① 根據隱藏規則 cur 要麼無孩子，要麼只有一個孩子。

　　② cur 無孩子時直接刪除即可，這不會打破平衡。

　　③ cur 有兩個孩子時，用後繼節點（或前驅）節點，然後調用函數自身刪除後繼（或前驅）節點。

　　註：③ 時，函數自身只會額外調用一次，因為後繼（或前驅）節點不可能有兩個孩子。

　　　　另外，後繼（或前驅）代替 cur 時，只代替 cur 的鍵，而不改變它們的顏色。

現在解決二（cur 是黑色）：

　　① cur 有兩個孩子：同一中的 ③ 情況，找後繼（或前驅）代替。

　　② cur 只有一個孩子：根據隱藏規則 ②，只需將紅孩子的鍵替換 cur 的鍵，然後刪除紅孩子即可（同樣不更改它們的顏色）。

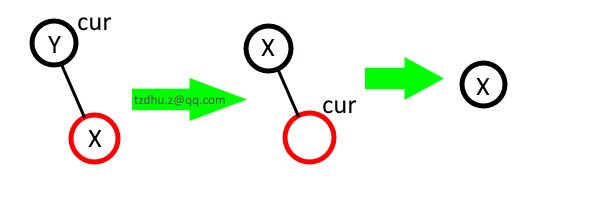
　　③ cur 沒有孩子：刪除 cur，則 par 在 cur 的支路會少一個黑節點，因此需要通過調整使得紅黑樹重歸於平衡，這是重點討論的。

現在，紅黑樹的刪除只剩下 ③，即 cur 是黑色且 cue 無孩子，再分類前進行簡單分析。

已經知道，刪除了 cur，則 par 在 cur 的支路會少一個黑節點，因此我們需要向 bro 所在的支路 “借” 一個節點一補充 par 在 cur 支路缺少的黑節點。

如何 “借”？若無法 “借” 又該怎麼辦？“借” 到了又該怎麼處理？這就是接下來分類討論的情況。

因此對於 cur 是黑色且無孩子的情況分為以下幾類：

　　① bro 是紅色。

　　② bro 是黑色但 bro 的孩子有紅色（分為左孩子是紅色或右孩子是紅色，實際上都為紅）。

　　③ bro 是黑色但 par 是紅色。

　　④ bro 是黑色，par 也是黑色（可知 bro 一定無孩子，看規則 ⑤）。

現在解決這些情況即可（現在假設 cur 是左孩子，若是右孩子，則於此左右對稱，交予讀者自行思考（筆者代碼中用 bool 變數 isLeft 來進行統一處理））。

　　解決 ①：直接看圖：

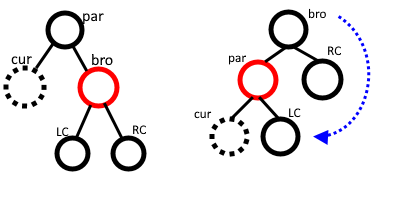
　　　　cur 是被刪除的節點，因此 cur 不參與調整。

　　　　將 par 左旋（若 cur 是右孩子則是右旋，後序不特地強調 cur 是右孩子的情況），然後將 bro 重新指向 LC 即可。

　　　　這時你可能發現 par 左子樹黑節點任然少一個，並未平衡，怎麼辦？這個時候滿足情況 ③，因此交給後面的情況處理即可。

　　解決 ②：LC 或者 RC 是紅色的情況在下圖統一給出（註意 cur 是左孩子，右孩子時應該怎麼做自行觀察）：

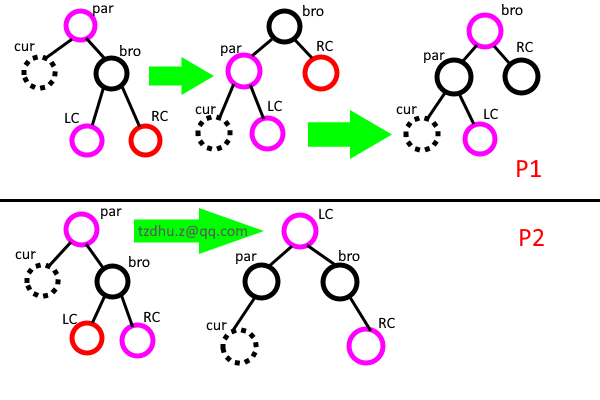
　　　　紫色代表節點任意色。

　　　　看 P1：RC 是紅色，則左旋 bro，然後將 bro 變為 par 的顏色，然後將 par 和 RC 變黑色即可。

　　　　看 P2：LC 是紅色，按圖中方法將 LC 上提，將 LC 變為 par 的顏色，再將 par 變黑色即可。圖示調整已經平衡可直接退出。

　　　　註：bro 孩子有一個紅色，則另一個一定是紅色或者空（黑色）（看規則 ⑤）。

　　解決 ③：par 是紅色時：

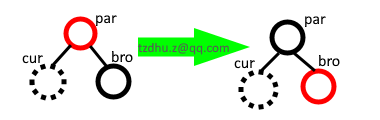
　　　　由於排除了 ② 情況，則 bro 的孩子一定為黑色（而且一定是空，看規則 ⑤），因此交換 par 和 bro 的顏色即可平衡。

　　解決 ④：par 是黑，且 bro 是黑（bro 一定無孩子，因為排除了 ② 情況，且看規則 ⑤）：

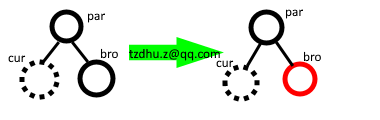
　　　　由於此時無法借到紅孩子，因此讓 bro 變紅，此時 par 左右子樹平衡，但是！！！！

　　　　但是 par 的父親在 par 支路上的黑節點少了！因此借紅孩兒的事情交給 par 處理，即 cur 指向 par，bro 指向 par 的兄弟，繼續回溯即可。

　　　　註意：若 par 沒有父親了怎麼辦（即 par 是根節點）? 那不就太好了嗎，省得回溯了，直接退出就可以了呀（所以寫代碼註意此情況！）！！！

　　至此，紅黑樹插入、刪除情況講解完，最後給出 c++ 代碼。

測試代碼 main.cpp：

#include <iostream>
#include "RBTree.h"

using std::cout;
using std::endl;

int main()
{
    RBTree<int> rbt;

    auto il = { 12,1,9,2,0,11,7,19,4,15,18,5,14,13,10,16,6,3,8,17 };
    cout << "After insert 12,1,9,2,0,11,7,19,4,15,18,5,14,13,10,16,6,3,8,17：" << endl;
    for (auto& x : il) rbt.insert(x);
    rbt.levelTraversal();
    cout << endl << endl;
    auto Del = [&rbt](int x)
    {
        cout << "After erase " << x << "：" << endl;
        rbt.erase(x);
        rbt.levelTraversal();
        cout << endl << "level: " << rbt.level() << endl << endl;
    };
    for (auto& x : il) Del(x);

    return 0;
}

頭文件 RBTree.h：

#pragma once
#ifndef __RBTREE_H__
#define __RBTREE_H__


#include "BinaryTreeOperations.h"
template<typename _Ty>
class RBTree
{
private:
    enum class Color :bool { RED = 0, BLACK };
    struct Node
    {
        _Ty key;
        Node* left = nullptr;
        Node* right = nullptr;
        Node* parent = nullptr;
        Color color = Color::RED;
        Node(const _Ty& _key) :key(_key) {}
    };

public:
    RBTree() = default;
    ~RBTree() { BTO::clear(root); size_n = 0; }
    void clear() noexcept { BTO::clear(root); size_n = 0; }

    void preorderTraversal() { BTO::preorderTraversal(root, drawData); }
    void inorderTraversal() { BTO::inorderTraversal(root, drawData); }
    void postorderTraversal() { BTO::postorderTraversal(root, drawData); }
    void iterativePreorderTraversal() { BTO::iterativePreorderTraversal(root, drawData); }
    void iterativeInorderTraversal() { BTO::iterativeInorderTraversal(root, drawData); }
    void iterativePostorderTraversal() { BTO::iterativePostorderTraversal(root, drawData); }
    void levelTraversal() { BTO::levelTraversal(root, drawData); }

    Node* find(const _Ty& _key) { return BTO::find(root, _key); }
    Node* iterativeFind(const _Ty& _key) { return BTO::iterativeFind(root, _key); }
    Node* findMaximum() { return BTO::findMaximum(root); }
    Node* findMinimum() { return BTO::findMinimum(root); }
    size_t level() { return BTO::getLevel(root); }
    size_t size() const { return size_n; }

    void insert(const _Ty&);
    bool erase(const _Ty&);
    void erase(Node*);

private:
    static void drawData(const Node* _node) { std::cout << _node->key << " "; }

private:
    size_t size_n = 0;
    Node* root = nullptr;
};

template<typename _Ty>
void RBTree<_Ty>::insert(const _Ty& _key)
{
    auto ret = BTO::insert(root, _key);
    if (ret.second) ++size_n;
    else return;
    auto cur = ret.first;
    if (cur->parent == nullptr) cur->color = Color::BLACK;
    if (cur->parent == nullptr || cur->parent->color == Color::BLACK) return;

    while (cur->parent != nullptr && cur->parent->color == Color::RED && cur->parent != root)
    {
        bool parIsRight = cur->parent == cur->parent->parent->right ? true : false;
        auto uncle = parIsRight ? cur->parent->parent->left : cur->parent->parent->right;
        if (uncle != nullptr && uncle->color == Color::RED)
        {
            cur->parent->color = Color::BLACK;
            uncle->color = Color::BLACK;
            cur->parent->parent->color = Color::RED;
            cur = cur->parent->parent;
        }
        else
        {
            if (parIsRight)
            {
                if (cur == cur->parent->left) cur = BTO::rightRotate(cur->parent)->right;
                cur = BTO::leftRotate(cur->parent->parent);
                cur->left->color = Color::RED;
                cur->color = Color::BLACK;
            }
            else
            {
                if (cur == cur->parent->right) cur = BTO::leftRotate(cur->parent)->left;
                cur = BTO::rightRotate(cur->parent->parent);
                cur->right->color = Color::RED;
                cur->color = Color::BLACK;
            }
            if (cur->parent == nullptr) root = cur;
            return;
        }
    }
    root->color = Color::BLACK;
}

template<typename _Ty>
bool RBTree<_Ty>::erase(const _Ty& _key)
{
    bool succeed = false;
    Node* del = BTO::find(root, _key);
    if (del != nullptr)
    {
        erase(del);
        succeed = true;
    }
    return succeed;
}

template<typename _Ty>
void RBTree<_Ty>::erase(Node* _node)
{
    if (_node == nullptr) return;
    --size_n;
    if (_node->color == Color::RED)
    {
        if (_node->left == nullptr && _node->right == nullptr)
        {
            if (_node == _node->parent->left) _node->parent->left = nullptr;
            else _node->parent->right = nullptr;
            delete _node;
        }
        else
        {
            auto del = BTO::findMinimum(_node->right);
            _node->key = del->key;
            ++size_n;
            erase(del);
        }
    }
    else
    {
        if (_node->right == nullptr && _node->left == nullptr)
        {
            Node* par = _node->parent;
            if (par == nullptr)
            {
                delete root;
                root = nullptr;
                return;
            }
            bool isLeft = _node == par->left ? true : false;
            isLeft ? par->left = nullptr : par->right = nullptr;
            delete _node;
            while (true)
            {
                Node* bro = isLeft ? par->right : par->left;
                if (bro->color == Color::RED)
                {
                    isLeft ? BTO::leftRotate(par) : BTO::rightRotate(par);
                    par->color = Color::RED;
                    bro->color = Color::BLACK;
                    if (bro->parent == nullptr) root = bro;
                    bro = isLeft ? par->right : par->left;
                }
                if (bro->color == Color::BLACK)
                {
                    if ((isLeft ? bro->left : bro->right) != nullptr && (isLeft ? bro->left : bro->right)->color == Color::RED)
                    {
                        Node* temp = isLeft ? bro->left : bro->right;
                        isLeft ? bro->left = nullptr : bro->right = nullptr;
                        isLeft ? par->right = nullptr : par->left = nullptr;
                        isLeft ? temp->right = bro : temp->left = bro;
                        bro->parent = temp;
                        if (par == par->parent->left) par->parent->left = temp;
                        else par->parent->right = temp;
                        temp->parent = par->parent;
                        isLeft ? temp->left = par : temp->right = par;
                        par->parent = temp;
                        temp->color = par->color;
                        par->color = Color::BLACK;
                        return;
                    }
                    else if ((isLeft ? bro->right : bro->left) != nullptr && (isLeft ? bro->right : bro->left)->color == Color::RED)
                    {
                        Node* temp = isLeft ? bro->right : bro->left;
                        isLeft ? BTO::leftRotate(par) : BTO::rightRotate(par);
                        bro->color = par->color;
                        par->color = Color::BLACK;
                        temp->color = Color::BLACK;
                        return;
                    }
                    else if (par->color == Color::RED)
                    {
                        par->color = Color::BLACK;
                        bro->color = Color::RED;
                        return;
                    }
                    else
                    {
                        bro->color = Color::RED;
                        if (par->parent != nullptr) isLeft = par == par->parent->left ? true : false;
                        else return;
                        par = par->parent;
                    }
                }
            }
        }
        else if (!(_node->right != nullptr && _node->left != nullptr))
        {
            if (_node->right != nullptr)
            {
                Node* del = _node->right;
                _node->key = del->key;
                _node->right = nullptr;
                delete del;
            }
            else
            {
                Node* del = _node->left;
                _node->key = del->key;
                _node->left = nullptr;
                delete del;
            }
        }
        else
        {
            auto del = BTO::findMinimum(_node->right);
            _node->key = del->key;
            ++size_n;
            erase(del);
        }
    }
}


#endif // !__RBTREE_H__