一.矩陣乘法 設矩陣A,B 滿足 ：A的列數==B的行數 矩陣乘法的運算規則： 將A矩陣的每一行乘以B矩陣的每一列 * == == 二.斐波那契數列的矩陣推導 首先我們想 Fib[i]=Fib[i-1]+Fib[i-2]; 所以斐波那契數列的第i項之與兩個數也就是Fib[i-1]+Fib[i-2]有 ...
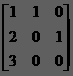
一.矩陣乘法
設矩陣A,B 滿足 ：A的列數==B的行數
矩陣乘法的運算規則：
將A矩陣的每一行乘以B矩陣的每一列
*
==
==
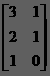
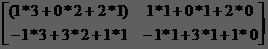
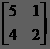
二.斐波那契數列的矩陣推導
首先我們想
Fib[i]=Fib[i-1]+Fib[i-2];
所以斐波那契數列的第i項之與兩個數也就是Fib[i-1]+Fib[i-2]有關
那麼我們可以設第一個矩陣
M1=
因為我們需要利用矩陣推出斐波那契的第n項
所以我們設M1的下一項為M3
則M3=
（也就是讓M1的下標整體後移一位）
那麼現在我們需要一個過渡矩陣M2來實現這個從M1到M3的操作
因為M1是一個1*2的矩陣
M3也是一個1*2的矩陣
那麼M2一定是一個2*2的矩陣
(原因：1.M1的列要和M2的行相等
2.M3的列數是2)
設M2=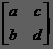
所以
a*fi-2+b*fi-1==fi-1①
c*fi-2+d*fi-1==fi②
這個式子看上去是不能解的
但是我們想一下
當a==0&&b==1的時候①成立
當c==1&&d==1的時候②成立（Fib[i]=Fib[i-1]+Fib[i-2]）
所以我們很容易的得到矩陣M2
M2=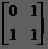
三.一道簡單的例題
設fi=fi-1+2fi-2+3fi-3
按照上面的方法求出M1,M2,M3
提示：矩陣推導的時候不帶繫數
（建議先做再看題解）
解：
設M1=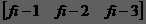
M3=
則M2一定是一個3*3的矩陣
設M2=
則a*fi-1+b*fi-2+c*fi-3==fi== fi-1+2fi-2+3fi-3
d*fi-1+e*fi-2+f*fi-3==fi-1
g*fi-1+h*fi-2+i*fi-3==fi-2
易得 a==1,b==2,c==3
d==1,e==0,f==0
g==0,h==0,i==0
所以
M2=
