樹(tree) [一]

来源:https://www.cnblogs.com/fly-home/p/18166700
-Advertisement-
Play Games

樹(tree) [一] 基本概念： ​ 日常生活中，很多數據的組織形式本質上是一棵樹。比如一個公司中的職員層級關係、一個學校中的院系層級關係、淘汰賽中的各次比賽隊伍、一個家族中的族譜成員關係等都是樹狀邏輯結構。由於樹狀結構表現出來都是具有層次的，因此也被稱為層次結構。 樹是一種非線性結構（一對多）， ...


樹(tree) [一]

基本概念：

​ 日常生活中，很多數據的組織形式本質上是一棵樹。比如一個公司中的職員層級關係、一個學校中的院系層級關係、淘汰賽中的各次比賽隊伍、一個家族中的族譜成員關係等都是樹狀邏輯結構。由於樹狀結構表現出來都是具有層次的，因此也被稱為層次結構。

樹是一種非線性結構（一對多），其嚴格的數學定義是：如果一組數據中除了第一個節點（第一個節點稱為根節點，沒有直接前驅節點）之外，其餘任意節點有且僅有一個直接前驅，有零個或多個直接後繼==，這樣的一組數據形成一棵樹。樹中的數據元素之間的邏輯關係是一對多的。

​ 樹就是n個結點的有限集，當n=0的時候，此時樹就被稱為空樹。任意的非空樹中有且只有一個特定的結點，該結點被稱為根或稱為根結點，也就是n = 1。

​ 當n>1的時候，其餘的結點可以分為m個（m>1）互不相交的有限集 T1、T2、T3.........Tm ，每個集合也被稱為一棵樹，就是根的子樹。

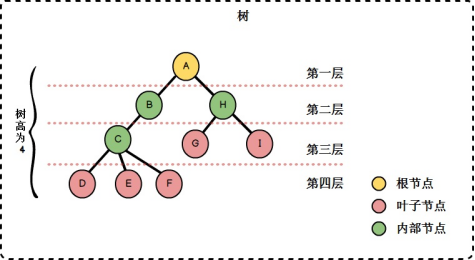
image

​ 對於樹狀結構，除了*根結點*之外，其餘的結點都可以分為多個不相交的*子樹*，具體如下所示:

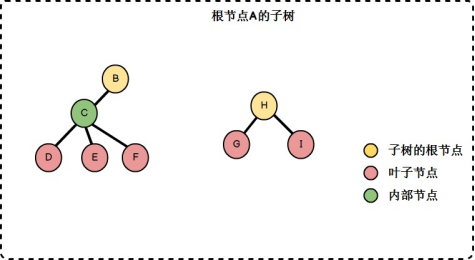
image

​ 可以看到，結點A就是根結點，根結點A下麵有兩個子樹，分別是子樹B和子樹H，另外結點B和H都是根結點A的子結點。

​ 如果一個結點有子樹，則該結點就被稱為子樹的“*雙親*”，該結點的子樹就被稱為結點的“*孩子*”，另外，具有相同結點的子樹就被稱為“*兄弟*”。如下圖所示：

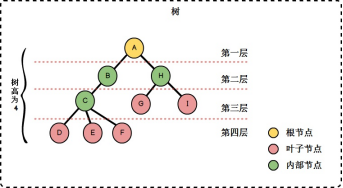
image

​ 可以看到，結點D的祖先為A、B、C，結點G的祖先為H、A，另外對於子樹B而言，結點C、D、E、F都是結點B的子孫。

  • 樹是分層結構，一般把樹的根結點稱為第一層，其餘的子結點的層次就是在上一層的基礎上+1，另外一般把樹的最大層數稱為*樹的深度*。樹的深度也被稱為樹的高度。

二叉樹：

概念：

​ 二叉樹是另一種樹狀結構，*二叉樹的特點就是每個結點至多有兩顆子樹*（每個結點的度不會超過2），並且二叉樹的子樹是*有左右之分*，如果有兩顆子樹，就分別叫做左子樹和右子樹，而且二叉樹的子樹是有次序的，不能隨意更改的，所以*二叉樹也屬於有序樹*，也就意味著哪怕二叉樹只有一個子樹，也要區分到底是左子樹還是右子樹。

​ 二叉樹也是n個（n>=0）結點的有限集，一般二叉樹有5種形式，分別是空樹、根結點（ROOT）、有根結點和左子樹以及右子樹、左子樹（Left Child Tree）、右子樹（Right Child Tree）。

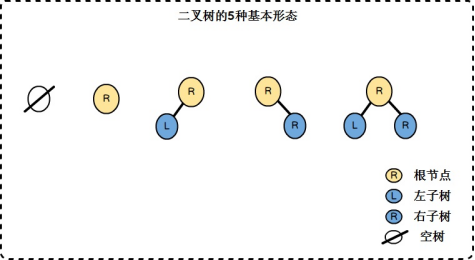
image

二叉樹分類：

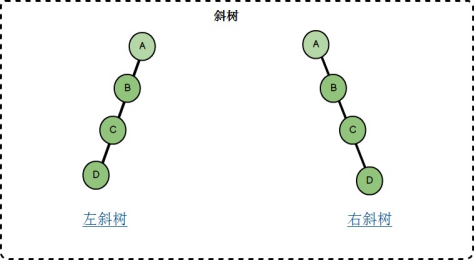
  • 斜樹：

    ​ 一般只有左子樹的二叉樹被稱為*左斜樹*，一般只有右子樹的二叉樹被稱為*右斜樹*，可以看到斜樹退化為線性結構，所以斜樹是沒有體現二叉樹的性能。

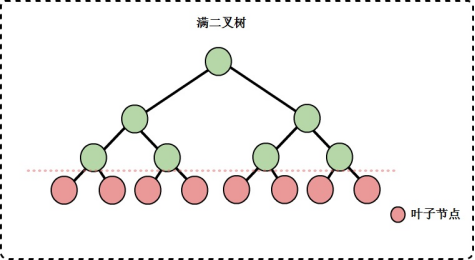
image

  • 滿二叉樹：

image

image

  • 完全二叉樹：

​ 對於一顆樹而言，完全二叉樹指的是只有樹的最下麵2層的結點的度可以小於2，並且結點的編號也是按照從上到下，從左到右的順序進行排列，最下麵一層的葉子結點都集中在左樹。

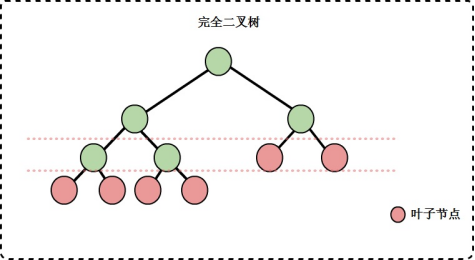
image

註意： 滿二叉樹一定是完全二叉樹，但是完全二叉樹不一定是滿二叉樹

  • 二叉查找樹：

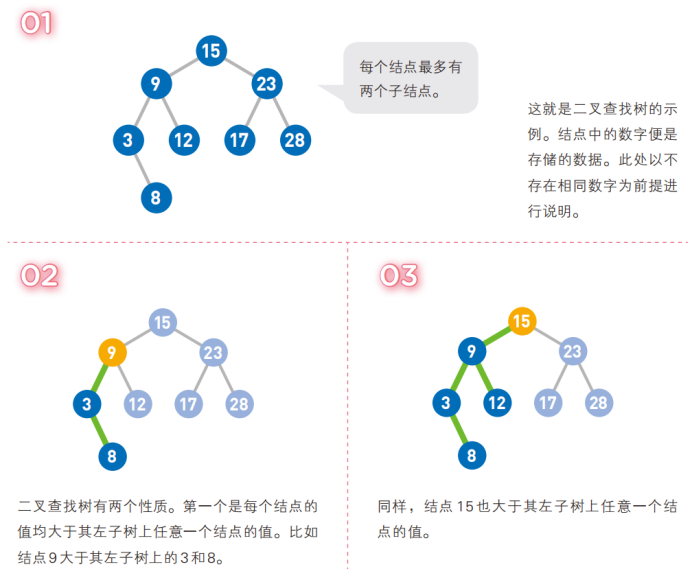
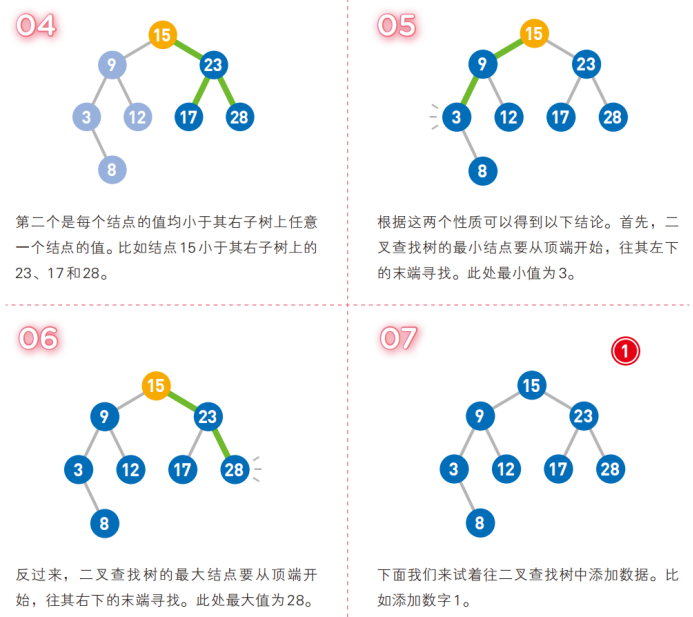
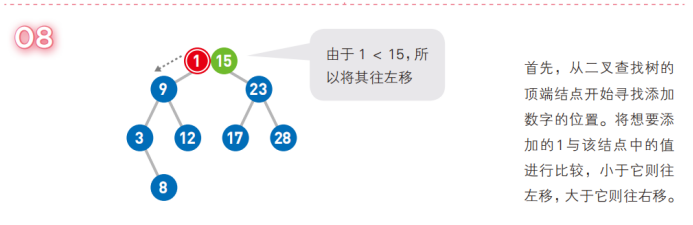
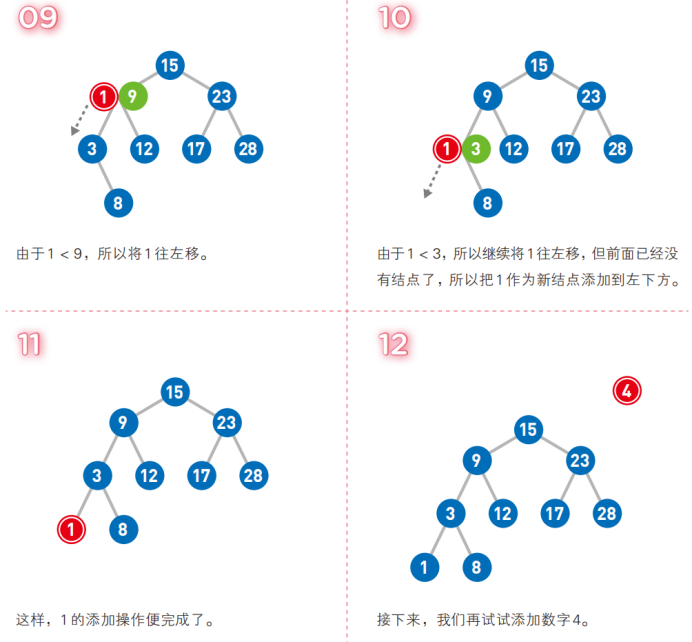
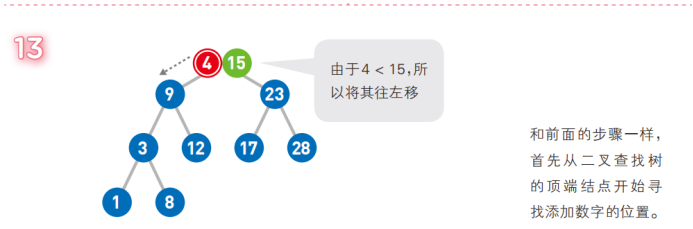
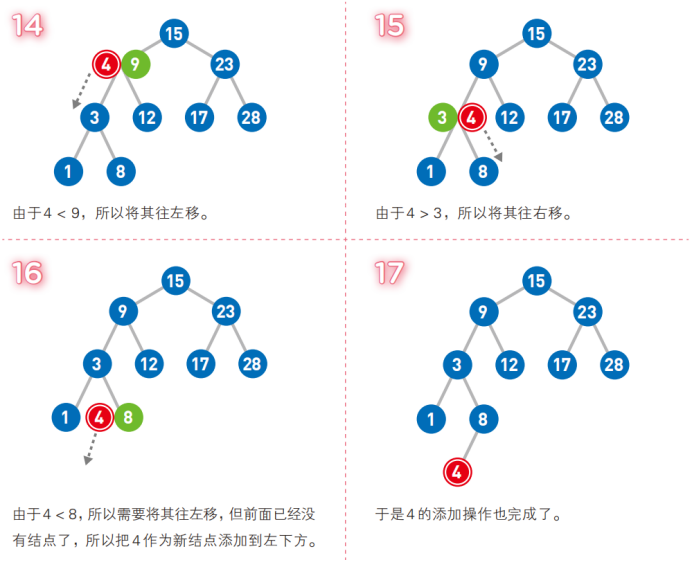
​ 二叉查找樹英文縮寫為*BST樹*（Binary Search Tree），一般也被稱為二叉搜索樹或者二叉排序樹，二叉查找樹的結點是有*鍵值key的*，如果二叉查找樹不是空樹則需要遵循以下的特點：

  1. 如果二叉查找樹有左子樹，則左子樹的結點的鍵值key要小於左子樹的根結點的鍵值key
  2. 如果二叉查找樹有右子樹，則右子樹的結點的鍵值key要大於右子樹的根結點的鍵值key
  3. 對於二叉查找樹而言，左子樹和右子樹也分別是二叉查找樹。

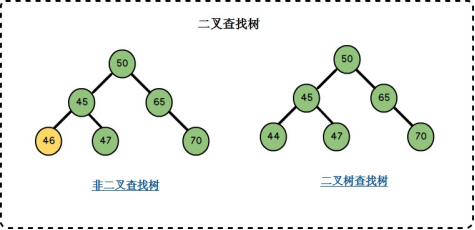
image

可以看到，左子樹的結點的鍵值都是小於右子樹，二叉查找樹的結點的鍵值key是不重覆的。

image

image

image

image

image

image

image

image

image

  • 平衡二叉樹：

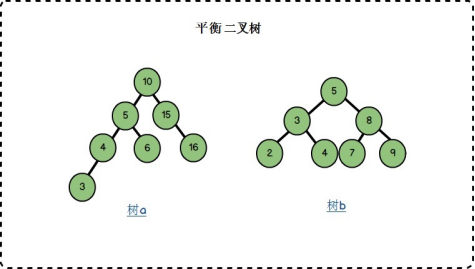
​ 平衡二叉樹也是有序樹，指的是樹中任一結點的左子樹和右子樹的深度之差不超過1，如下圖所示：

image

二叉樹的性質：

  • *非空二叉樹中的葉子結點數量等於雙分支結點數量+1*，雙分支結點指的是就是度為2的結點，假設二叉樹的葉子結點數量為n0,二叉樹中單分支結點的數量為n1，二叉樹中雙分支結點的數量為n2，則二叉樹中結點的總數 = n0 + n1 + n2。

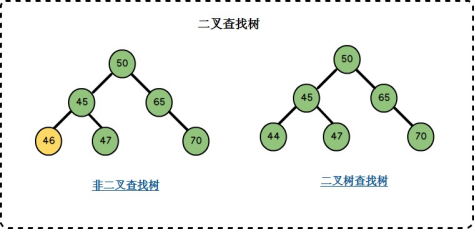
image

​ 可以看到，上圖二叉查找樹中葉子結點的數量為3，度為1的結點的數量為1，度為2的結點數量為2，所以該二叉查找樹的結點總數為6，和圖中結點數量一致。

  • 二叉樹的第i層上*最多*有2的(i - 1)次方（i≥1）個結點，因為二叉樹結點最多的情況就是滿二叉樹。

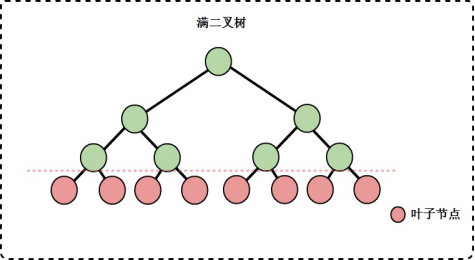
image

​ 可以看到，滿二叉樹此時一共有4層，也就是二叉樹的高度為4，假設要計算二叉樹第4層的結點數量，則帶入公式之後得到的結果為8，和圖中結點數量一致。

  • 高度為h的二叉樹*最多*有2的h次方 - 1（h≥1）個結點。滿二叉樹就是結點最多的二叉樹，所以換句話說，滿二叉樹前h層結點的數量為2的h次方 - 1（h≥1）。

二叉樹的存儲結構

  • 順序結構

​ 二叉樹的順序結構就是採用一組地址連續的記憶體單元（數組）按照從上到下，從左到右的順序依次存儲二叉樹中的結點，也就是把二叉樹中編號為i的結點存儲在數組下標為i-1的元素空間中。

​ 如果按照二叉樹的性質而言，滿二叉樹以及完全二叉樹使用順序存儲比較合適，好處是可以最大程式的節約記憶體空間，並且可以利用數組下標查找數據。

​ 對於一般的二叉樹而言，也可以使用順序結構進行存儲，為了可以使用數組來表示結點的邏輯關係，需要數組的一些元素空間來存儲空結點，會導致浪費空間。0表示不存在的空結點。如下圖所示：

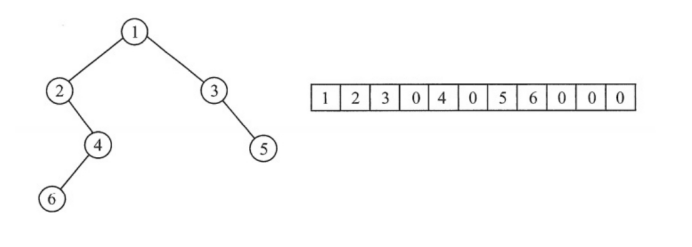
image

  • 鏈式結構

    ​ 鏈式結構就可以有效的解決數組中存儲空結點的問題，鏈式結構不受記憶體的限制，由於一個結點最多可能存在兩個子結點，所以應該採用雙向不迴圈鏈表的方案來實現。

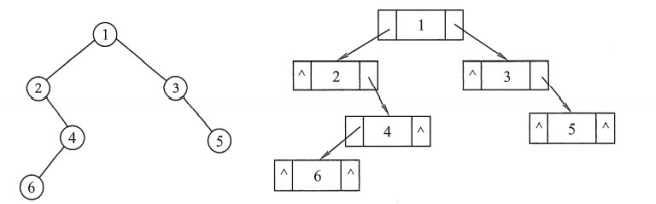
image

二叉樹的遍歷說明

​ 通過遍歷二叉樹可以得到二叉樹的所有信息，對二叉樹做出全面的瞭解，對於二叉樹遍歷結點而言，絕大多數是採用二叉查找樹（BST樹）來實現，接下來就以二叉查找樹為例進行講解：

/********************************************************************************************************
*
*
* 設計BST二叉查找樹的介面，為了方便對二叉樹進行節點的增刪，所以採用雙向不迴圈鏈表實現，每個節點內部都需要
* 有2個指針，分別指向該節點的左子樹(lchild)和右子樹(rchild)
*
* 
*
* Copyright (c)  2023-2024   [email protected]   All right Reserved
* ******************************************************************************************************/
//指的是BST樹中的結點有效鍵值的數據類型，用戶可以根據需要進行修改
typedef int  DataType_t;


//構造BST樹的結點,BST樹中所有結點的數據類型應該是相同的
typedef struct BSTreeNode
{
	DataType_t  		 data; 	//節點的鍵值
	struct BSTreeNode	*lchild; 	//左子樹的指針域
	struct BSTreeNode	*rchild; 	//右子樹的指針域

}BSTnode_t;

  1. 創建BST樹的根節點，並完成根節點的初始化

    //創建一個帶根節點的BST樹，對BST樹的根節點進行初始化
BSTnode_t * BSTree_Create(DataType_t KeyVal)
{
	//1.創建一個根結點並對根結點申請記憶體
	BSTnode_t *Root = (BSTnode_t *)calloc(1,sizeof(BSTnode_t));
	if (NULL == Root)
	{
		perror("Calloc memory for Root is Failed");
		exit(-1);
	}

	//2.對根結點進行初始化，根節點的2個指針域分別指向NULL
	Root->data = KeyVal;
	Root->lchild = NULL;
	Root->rchild = NULL;

	//3.把根結點的地址返回即可
	return Root;
}

  2. 創建BST樹中新的節點，並完成其的初始化（數據域 + 指針域）

    //創建新的結點，並對新結點進行初始化（數據域 + 指針域）
BSTnode_t * BSTree_NewNode(DataType_t KeyVal)
{
	//1.創建一個新結點並對新結點申請記憶體
	BSTnode_t *New = (BSTnode_t *)calloc(1,sizeof(BSTnode_t));
	if (NULL == New)
	{
		perror("Calloc memory for NewNode is Failed");
		return NULL;
	}

	//2.對新結點的數據域和指針域（2個）進行初始化
	New->data = KeyVal;
	New->lchild = NULL;
	New->rchild = NULL;

	return New;
}

  3. 向BST樹中加入節點 並且要遵循BST樹的特點。即：根節點的左子樹的鍵值都是比根節點小的，根節點的右子樹的鍵值都是比根節點大的

    //向BST樹中加入節點   規則：根節點的左子樹的鍵值都是比根節點小的，根節點的右子樹的鍵值都是比根節點大的
bool BSTree_InsertNode(BSTnode_t *Root,DataType_t KeyVal)
{

	//為了避免根節點地址丟失，所以需要對地址進行備份
	BSTnode_t *Proot = Root;


	//1.創建新節點並對新結點進行初始化
	BSTnode_t * New = BSTree_NewNode(KeyVal);
	if (NULL == New)
	{
		printf("Create NewNode Error\n");
		return false;
	}

	//2.此時分析當前的BST樹是否為空樹，有2種情況（空樹 or 非空樹）
	if (NULL == Root)
	{
		//此時BST樹為空樹，則直接把新節點作為BST樹的根節點
		Root = New;
	}
	else
	{
		while(Proot)
		{
			
			//新節點的鍵值和根節點的鍵值進行比較,如果相等則終止函數
			//因為BST樹不能存有相同的樹
			if (Proot->data == New->data)
			{
				printf("Can Not Insert,.....\n");
				return false;
			}
			//新節點的鍵值和根節點的鍵值進行比較,如果不相等繼續分析
			else
			{
				//新節點的鍵值小於根節點的鍵值，則把根節點的左子樹作為新的根
				if( New->data < Proot->data )
				{
					//如果左邊子樹為空，則直接插入新的節點
					if (Proot->lchild == NULL)
					{
						Proot->lchild = New;
						break;
					}

					Proot = Proot->lchild;

				}
				else
				{
					//如果右邊子樹為空，則直接插入新的節點
					if (Proot->rchild == NULL)
					{
						Proot->rchild = New;
						break;
					}

					Proot = Proot->rchild;
				}
			}
		}

	}

	return true;
}

    驗證結果：

    思考：如果按照思路把n個結點插入到二叉查找樹中，請問應該如何驗證程式的正確性???

    1. 需要包含drawtree.h頭文件，並需要把源文件和該頭文件處於同一個路徑中，使用雙引號包含，即："drawtree.h"

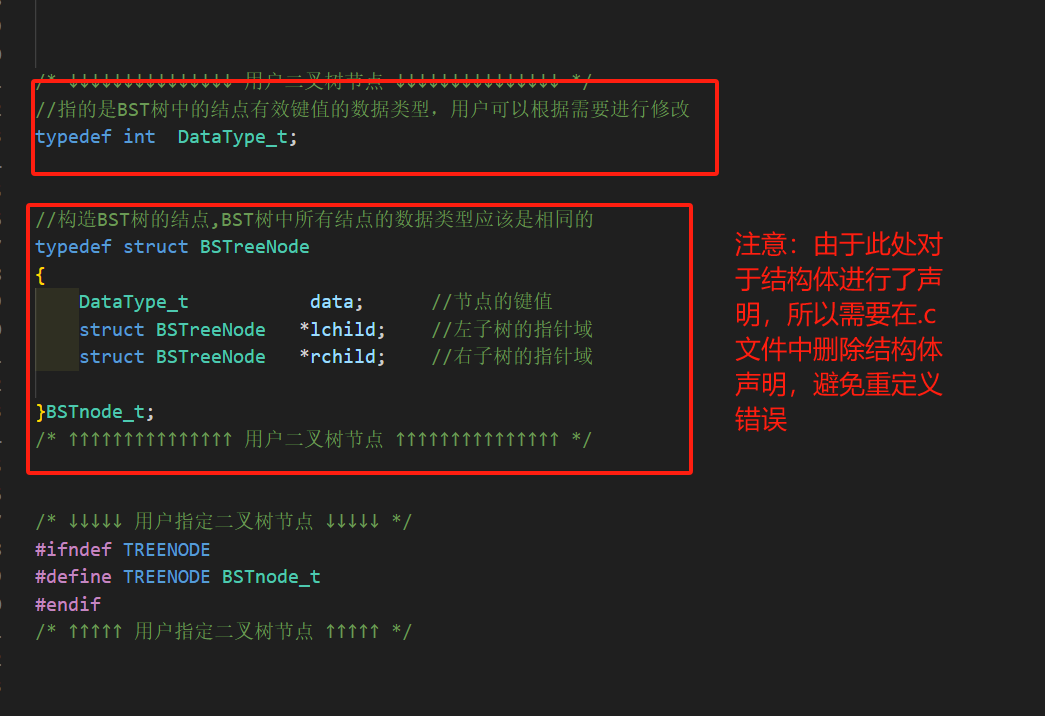
    2. 修改drawtree.h頭文件中關於二叉樹的數據類型以及二叉樹結點的類型，操作如下圖所示!image

    3. 在用戶設計的源文件中調用drawtree.h頭文件中的函數即可，然後把根結點傳入該函數！！ 即：在主函數中調用該函數。

    4. 編譯源程式，當編譯運行之後，會自動在當前目錄內生成一個網頁，打開網頁即可驗證！！

      image

  • drawtree.h頭文件如下：
///////////////////////////////////////////////////////////
//
//  Copyright(C), 2013-2021, GEC Tech. Co., Ltd.
//
//  文件: lab/tree/headers/drawtree.h
//  日期: 2017-9
//  描述: 使用C語言寫一頁webpage展示二叉樹
//
//  作者: 粵嵌科技  
//
///////////////////////////////////////////////////////////

#ifndef _DRAWTREE_H_
#define _DRAWTREE_H_

/* ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ 公共頭文件 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */
#include <time.h>
#include <fcntl.h>
#include <errno.h>
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <string.h>
#include <stdbool.h>
#include <strings.h>

#include <sys/stat.h>
#include <sys/types.h>

/* ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑ 公共頭文件 ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑ */

#define MAX(a, b) ({ \
		typeof(a) _a = a; \
		typeof(b) _b = b; \
		(void)(&_a == &_b);\
		_a > _b? _a : _b; \
		})



/* ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ 用戶二叉樹節點 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */
//指的是BST樹中的結點有效鍵值的數據類型，用戶可以根據需要進行修改
typedef int  DataType_t;


//構造BST樹的結點,BST樹中所有結點的數據類型應該是相同的
typedef struct BSTreeNode
{
	DataType_t  		 data; 		//節點的鍵值
	struct BSTreeNode	*lchild; 	//左子樹的指針域
	struct BSTreeNode	*rchild; 	//右子樹的指針域

}BSTnode_t;
/* ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑ 用戶二叉樹節點 ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑ */


/* ↓↓↓↓↓ 用戶指定二叉樹節點 ↓↓↓↓↓ */
#ifndef TREENODE
#define TREENODE BSTnode_t
#endif
/* ↑↑↑↑↑ 用戶指定二叉樹節點 ↑↑↑↑↑ */








/* ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ 預設二叉樹節點 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */
typedef struct _tree_node
{
	int data;
	struct _tree_node *lchild;
	struct _tree_node *rchild;

#ifdef AVL
	int height;
#endif

#ifdef RB
	struct _tree_node *parent;
	int color;
#endif
}_treenode, *_linktree;

// #ifndef TREENODE
// #define TREENODE Tnode_t
// #endif

/* ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑ 預設二叉樹節點 ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑ */


/* ↓↓↓↓↓↓↓↓↓↓↓↓↓ 畫網頁相關演算法代碼 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */

#ifndef QUEUE_TREENODE_DATATYPE
#define QUEUE_TREENODE_DATATYPE TREENODE *
#endif

typedef QUEUE_TREENODE_DATATYPE qn_datatype;

struct _queue_node
{
	qn_datatype data;
	struct _queue_node *next;

};

typedef struct
{
	struct _queue_node *front;
	struct _queue_node *rear;
#ifdef QUEUE_SIZE
	int size;
#endif
}_queuenode, *_linkqueue;


static _linkqueue init_queue(void)
{
    _linkqueue q = (_linkqueue)malloc(sizeof(_queuenode));
	q->front = q->rear =
		(struct _queue_node *)malloc(sizeof(struct _queue_node));
	q->rear->next = NULL;

	return q;
}

static bool is_empty_q(_linkqueue q)
{
	return (q->front == q->rear);
}

/* ↓↓↓↓↓↓↓↓↓↓↓↓↓ 畫網頁相關演算法代碼 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */
static bool out_queue(_linkqueue q, qn_datatype *pdata)
{
	if(is_empty_q(q))
		return false;

	struct _queue_node *p = q->front;

	q->front = q->front->next;
	free(p);
	*pdata = q->front->data;

	return true;
}

static bool en_queue(_linkqueue q, qn_datatype data)
{
	struct _queue_node *pnew;
	pnew = (struct _queue_node *)malloc(sizeof(struct _queue_node));
	if(pnew == NULL)
		return false;

	pnew->data = data;
	pnew->next = NULL;

	q->rear->next = pnew;
	q->rear = pnew;

	return true;
}

#ifdef QUEUE_SIZE
int queue_size(_linkqueue *q)
{
	return q->size;
}
#endif
/* ↓↓↓↓↓↓↓↓↓↓↓↓↓ 畫網頁相關演算法代碼 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */


static void pre_travel(TREENODE *root, void (*handler)(TREENODE *))
{
	if(root == NULL)
		return;
	
	handler(root);
	pre_travel(root->lchild, handler);
	pre_travel(root->rchild, handler);
}

static void mid_travel(TREENODE *root, void (*handler)(TREENODE *))
{
	if(root == NULL)
		return;
	
	mid_travel(root->lchild, handler);
	handler(root);
	mid_travel(root->rchild, handler);
}

static void post_travel(TREENODE *root, void (*handler)(TREENODE *))
{
	if(root == NULL)
		return;

	post_travel(root->lchild, handler);
	post_travel(root->rchild, handler);
	handler(root);
}

/* ↓↓↓↓↓↓↓↓↓↓↓↓↓ 畫網頁相關演算法代碼 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */
static void level_travel(TREENODE *root, void (*handler)(TREENODE *))
{
	if(root == NULL)
		return;

    _linkqueue q;
	q = init_queue();

	en_queue(q, root);

    TREENODE *tmp;
	while(1)
	{
		if(!out_queue(q, &tmp))
			break;

		handler(tmp);

		if(tmp->lchild != NULL)
			en_queue(q, tmp->lchild);
		if(tmp->rchild != NULL)
			en_queue(q, tmp->rchild);
	}
}
/* ↓↓↓↓↓↓↓↓↓↓↓↓↓ 畫網頁相關演算法代碼 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */
static char page_begin[] = "<html><head><title>tree map"
                           "</title></head><body>"
			   "<table border=0 cellspacing"
                           "=0 cellpadding=0>";
static char line_begin[] = "<tr>";
static char line_end  [] = "</tr>";
static char space     [] = "<td>&nbsp;</td>";
static char underline [] = "<td style=\"border-bottom:"
	 		   "1px solid #58CB64\">&nbsp;"
                           "</td>";

#ifdef RB
static char data_begin_red[] = "<td bgcolor=\"#FF0000\";style="
			       "\"border:1px sol"
                               "id #58CB64;background-colo"
                               "r:#DDF1D8;PADDING:2px;\" t"
                               "itle=\"level: 1\">";
static char data_begin_blk[] = "<td bgcolor=\"#000000\";style="
			       "\"border:1px sol"
                               "id #58CB64;background-colo"
                               "r:#DDF1D8;PADDING:2px;\" t"
                               "itle=\"level: 1\"><font color"
				"=\"#FFFFFF\">";
static char data_end_red[] = "</td>";
static char data_end_blk[] = "</font></td>";
#else
static char data_begin[] = "<td style=\"border:1px sol"
                           "id #58CB64;background-colo"
                           "r:#DDF1D8;PADDING:2px;\" t"
                           "itle=\"level: 1\">";
static char data_end  [] = "</td>";
#endif

static char page_end  [] = "</table></body></html>";

#define MAX_TREENODES_NUMBER 100
#define FILENAME 32

static int central_order[MAX_TREENODES_NUMBER];

static void putunderline(int fd, int num)
{
	int i;
	for(i=0; i<num; i++)
	{
		write(fd, underline, strlen(underline));
	}
}


static void putspace(int fd, int num)
{
	int i;
	for(i=0; i<num; i++)
	{
		write(fd, space, strlen(space));
	}
}
/* ↓↓↓↓↓↓↓↓↓↓↓↓↓ 畫網頁相關演算法代碼 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */
#ifdef RB
static void putdata(int fd, TREENODE * p)
{
	char s[50];
	bzero(s, 50);

	snprintf(s, 50, "%d", p->data);

	switch(p->color)
	{
	case RED:
		write(fd, data_begin_red, strlen(data_begin_red));
		write(fd, s, strlen(s));
		write(fd, data_end_red, strlen(data_end_red));
		break;
	case BLACK:
		write(fd, data_begin_blk, strlen(data_begin_blk));
		write(fd, s, strlen(s));
		write(fd, data_end_blk, strlen(data_end_blk));
	}
}
#else
static void putdata(int fd, int data)
{
	char s[50];
	bzero(s, 50);

	snprintf(s, 50, "%d", data);
	write(fd, data_begin, strlen(data_begin));
	write(fd, s, strlen(s));
	write(fd, data_end, strlen(data_end));
}
#endif

static int Index = 0;
static void create_index(TREENODE * root)
{
	if(Index >= MAX_TREENODES_NUMBER-1)
		return;

	central_order[Index++] = root->data;
}


static int get_index(int data)
{
	int i;
	for(i=0; i<100; i++)
	{
		if(central_order[i] == data)
			return i;
	}
	return -1;
}

/* ↓↓↓↓↓↓↓↓↓↓↓↓↓ 畫網頁相關演算法代碼 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */
static void data_leftside(int fd, TREENODE * root, int spaces)
{
	if(root == NULL)
		return;

	int s_line=0;

	if(root->lchild != NULL)
	{
		s_line = get_index(root->data)-
			 get_index(root->lchild->data)-1;
	}
	putspace(fd, spaces-s_line);
	putunderline(fd, s_line);
}


static int data_rightside(int fd, TREENODE * root)
{
	if(root == NULL)
		return 0;

	int s_line=0;

	if(root->rchild != NULL)
	{
		s_line = get_index(root->rchild->data)-
			 get_index(root->data)-1;
	}

	putunderline(fd, s_line);
	return s_line;
}


static void start_page(int fd)
{
	write(fd, page_begin, strlen(page_begin));
}

/* ↓↓↓↓↓↓↓↓↓↓↓↓↓ 畫網頁相關演算法代碼 ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓ */
static void end_page(int fd)
{
	write(fd, page_end, strlen(page_end));
}


static void draw(TREENODE * root)
{
	if(root == NULL)
		return;

	time_t t;
	time(&t);
	static char filename[FILENAME];
	bzero(filename, FILENAME);
	snprintf(filename, FILENAME, "%u.html", (unsigned)t);
	int fd = open(filename, O_CREAT | O_TRUNC | O_RDWR, 0644);
	if(fd == -1)
	{
		perror("open() failed");
		exit(1);
	}

	Index = 0;
	mid_travel(root, create_index);

    _linkqueue q = init_queue();

	TREENODE * tmp = root;
	int ndata = 1;

	start_page(fd);
	while(1)
	{
		write(fd, line_begin, strlen(line_begin));

		int i, n = 0;
		int nextline = 0;
		for(i=0; i<ndata; i++)
		{
			int index = get_index(tmp->data);

			data_leftside(fd, tmp, index-n);

			#ifdef RB
			putdata(fd, tmp);
			#else
			putdata(fd, tmp->data);
			#endif
			int rightline = data_rightside(fd, tmp);

			if(tmp->lchild != NULL)
			{
				nextline++;
				en_queue(q, tmp->lchild);
			}
			if(tmp->rchild != NULL)
			{
				nextline++;
				en_queue(q, tmp->rchild);
			}
			if(!out_queue(q, &tmp))
				return;

			n = index + rightline;
			n++;
		}
		write(fd, line_end, strlen(line_end));
		ndata = nextline;
	}
	end_page(fd);
	close(fd);
}
#endif

二叉樹的三種遍歷方法：前序遍歷、中序遍歷、後序遍歷

​ 對於二叉樹的遍歷，指的是從根結點出發，依次訪問二叉樹中所有的結點，每個結點只會被訪問一次，一共提供了三種方案實現二叉樹結點的遍歷：前序遍歷、中序遍歷、後序遍歷。

  • 前序遍歷（根結點--->左子樹--->右子樹） A B D G H C E I F

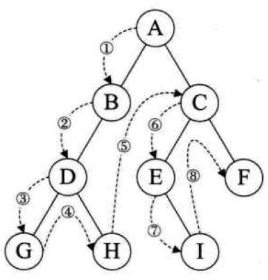
image

  • 中序遍歷（左子樹--->根結點--->右子樹） G D H B A E I C F

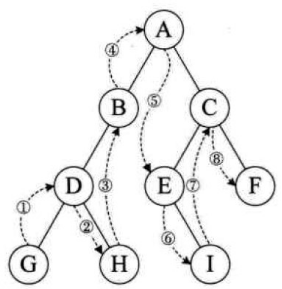
image

  • 後序遍歷（左子樹--->右子樹--->根結點） G H D B I E F C A

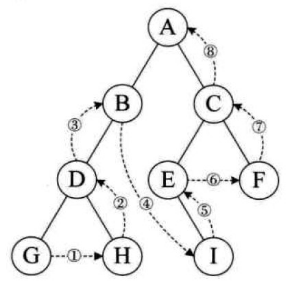
image

刪除二叉查找樹中的節點（參考）

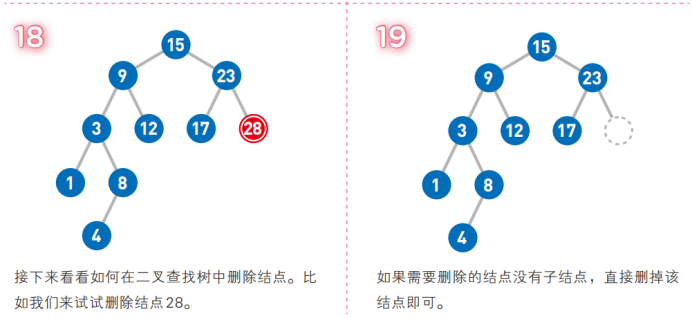
​ 從二叉查找樹刪除某個結點比插入結點要麻煩一點，但是刪除結點之後也必須遵循“小--中--大”的原則。刪除結點的時候就可能會出現以下幾種情況：

(1) 要刪除的結點的鍵值比根結點小，則在根結點的左子樹進行遞歸的刪除

(2) 要刪除的結點的鍵值比根結點大，則在根結點的右子樹進行遞歸的刪除

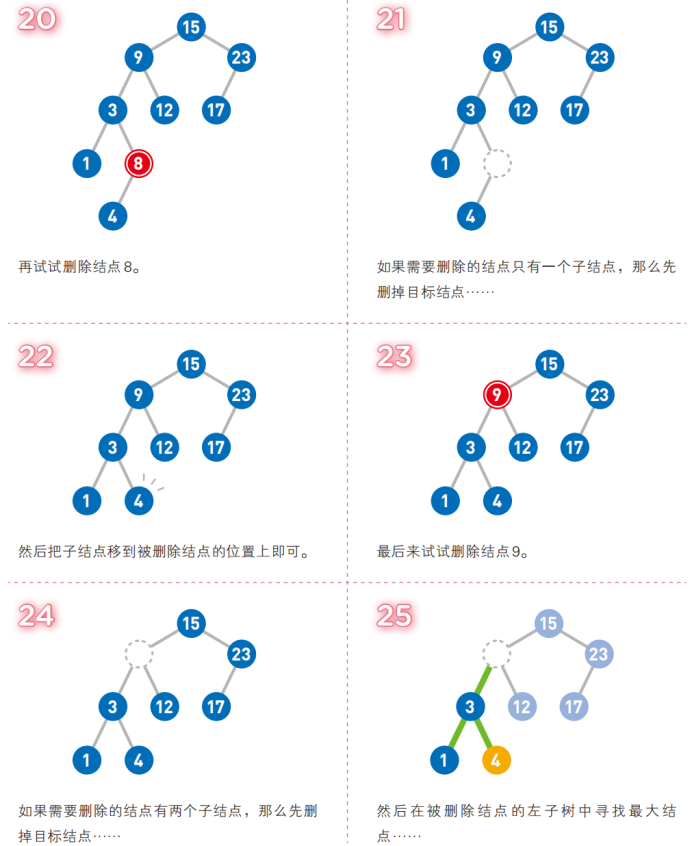
(3) 如果要刪除的結點恰好是根結點，也會遇到以下三種情況：

  1. 如果根結點有左子樹，需要從左子樹中找到鍵值最大的結點去替換根結點，然後在左子樹中把原來的鍵值最大的結點遞歸的刪掉

  2. 如果根結點有右子樹，需要從右子樹中找到鍵值最小的結點去替換根結點，然後在右子樹中把原來的鍵值最小的結點遞歸的刪掉

  3. 如果根結點沒有左子樹和右子樹，則直接把根結點刪掉

    例如：

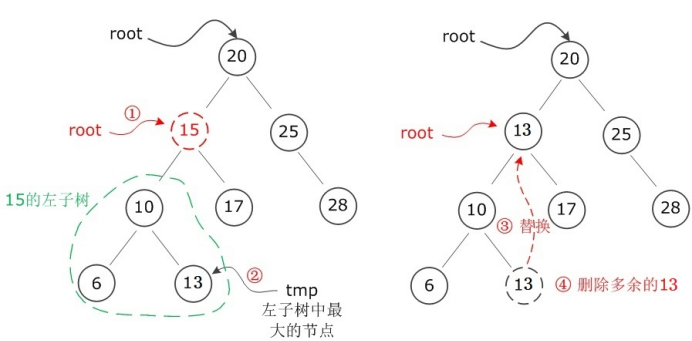
image

​ 可以看到，如果要刪除的結點是15，該結點有左子樹，所以需要從左子樹中找到鍵值最大的結點，也就是13，然後把13替換到15的位置，最後把多餘13刪掉即可。

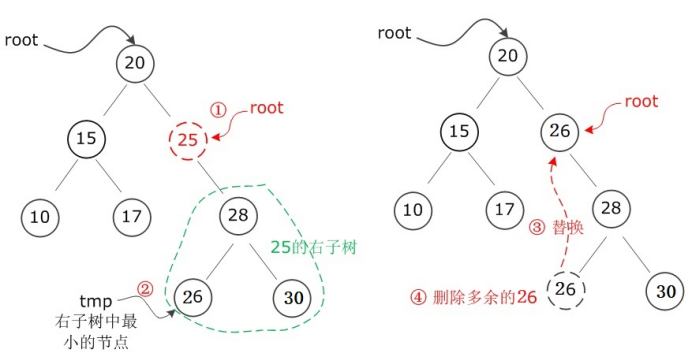
image

​ 可以看到，如果要刪除的結點是25，該結點有右子樹，所以需要從右子樹中找到鍵值最小的結點，也就是26，然後把26替換到25的位置，最後把多餘26刪掉即可。


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • C++ 多級繼承與多重繼承：代碼組織與靈活性的平衡
    C++ 多級繼承 多級繼承是一種面向對象編程（OOP）特性，允許一個類從多個基類繼承屬性和方法。它使代碼更易於組織和維護，並促進代碼重用。 多級繼承的語法 在 C++ 中，使用 : 符號來指定繼承關係。多級繼承的語法如下： class DerivedClass : public BaseClass1 ...
  • 【Flink入門修煉】2-3 Flink Checkpoint 原理機制
    如果讓你來做一個有狀態流式應用的故障恢復，你會如何來做呢？ 單機和多機會遇到什麼不同的問題？ Flink Checkpoint 是做什麼用的？原理是什麼？ ...
  • 萬字長文總結與剖析C語言關鍵字 -- <<C語言深度解剖>>
    C總結與剖析:關鍵字篇 -- <<C語言深度解剖>> 目錄C總結與剖析:關鍵字篇 -- <<C語言深度解剖>>程式的本質:二進位文件變數1.變數:記憶體上的某個位置開闢的空間2.變數的初始化3.為什麼要有變數4.局部變數與全局變數5.變數的大小由類型決定6.任何一個變數,記憶體賦值都是從低地址開始往高地 ...
  • mORMot2 獲取數據集1
    前言 整理這個官方翻譯的系列，原因是網上大部分的 tomcat 版本比較舊，此版本為 v11 最新的版本。 開源項目 從零手寫實現 tomcat minicat 別稱【嗅虎】心有猛虎，輕嗅薔薇。 系列文章 web server apache tomcat11-01-官方文檔入門介紹 web serv ...
  • 順序棧的介面程式
    順序棧的介面程式 目錄順序棧的介面程式頭文件創建順序棧入棧出棧利用棧將10進位轉16進位數驗證 頭文件 #include <stdio.h> #include <stdbool.h> #include <stdlib.h> 創建順序棧 // 指的是順序棧中的元素的數據類型，用戶可以根據需要進行修改 ...
  • C# - 能否讓 SortedSet.RemoveWhere 內傳入的委托非同步執行
    新改進提供的Taurus Rpc 功能，可以簡化微服務間的調用，同時可以不用再手動輸出模塊名稱，或調用路徑，包括負載均衡，這一切，由框架實現並提供了。新的Taurus Rpc 功能，將使得服務間的調用，更加輕鬆、簡約、高效。 ...
  • UOS 開啟 VisualStudio 遠程調試 .NET 應用之旅
    前言 在我們開發過程中基本上不可或缺的用到一些敏感機密數據，比如SQL伺服器的連接串或者是OAuth2的Secret等，這些敏感數據在代碼中是不太安全的，我們不應該在源代碼中存儲密碼和其他的敏感數據，一種推薦的方式是通過Asp.Net Core的機密管理器。 機密管理器 在 ASP.NET Core ...
  • Linux中atime,ctime與mtime的細節疑問總結
    在Linux文件系統中，每一個文件都有三個時間屬性，它們分別是atime,mtime,ctime,一般來說，atime比較好理解，但是很多時候，我們往往會混淆mtime和ctime這兩個時間屬性，或者搞不清楚兩者的區別。在展開介紹之前，我們先來看看如何查看文件的atime,mtime,ctime屬性 ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類