刷 Leetcode 總能遇到關於二分的題目,但是之前也只是草草地瞭解一下,每次在使用的時候都需要找模板,要不然就需要對於邊界條件進行調試,著實是很麻煩!!! 二分介紹: 首先來簡單介紹一下二分:二分查找也稱折半查找(Binary Search),它是一種效率較高的查找方法。但是,折半查找要求 線性 ...
刷 Leetcode 總能遇到關於二分的題目,但是之前也只是草草地瞭解一下,每次在使用的時候都需要找模板,要不然就需要對於邊界條件進行調試,著實是很麻煩!!!
二分介紹:
首先來簡單介紹一下二分:二分查找也稱折半查找(Binary Search),它是一種效率較高的查找方法。但是,折半查找要求 線性表 必須採用 順序存儲結構,而且表中元素按關鍵字有序排列。
優點:
- 比較次數少:二分查找每次將搜索範圍縮小一半,因此比較次數較少,查找速度快。
- 時間複雜度低:在有序數組中,二分查找的時間複雜度為O(log n),其中n為搜索範圍的大小。相比線性查找的O(n)時間複雜度,二分查找更高效。
- 可靠性高:由於二分查找是基於有序數組進行的,因此在數組有序的前提下,可以保證查找結果的準確性。
缺點:
- 要求有序數組:二分查找要求待查表為有序表,如果數組無序,則需要先進行排序操作,增加了額外的時間複雜度。
- 插入刪除困難:由於二分查找是基於有序數組進行的,插入和刪除操作會破壞數組的有序性,因此在插入和刪除元素時需要維護數組的有序性,增加了操作的複雜度。
在一段有序序列中尋找指定元素(或者該序列中不存在指定元素,返回小於等於指定元素的最大值)等等
二分法講解:
arr數組為有序序列
left: 左邊界
right:右邊界
mid = (left + right) / 2: 中間下標
迴圈條件: left .. right
上述為二分中的左邊界(left),右邊界(right),中間元素下標(mid).
二分法分類:
1.閉區間(左邊界 left = 0, 右邊界 right = arr.size() - 1)
先插入代碼:
// 1 2 3 5 6 8 9 10(有序數組中的元素)
int left = 0, right = arr.size() - 1;
int goal = 5;while(left <= right){
int mid = ( left + right) / 2;
if(goal > arr[mid]){
left = mid + 1;
}else{
right = mid - 1;
}
cout << "Left:" << left << " " << "Right:" << right << " " ;
}
cout << "結果是" << left << endl;
我們直接進行分析(先不要想為什麼這樣子,先跟著我的思路走):
(1)閉區間初始化:
left = 0, right = arr.size() - 1,則此時 left 和 right 代表的分別是數組序列的起始元素和末尾元素
(2)迴圈條件的設置:
迴圈結束的標誌是區間內沒有元素,因此只有當 left < right 的時候才會終止,因此設置 while(left <= right)
(3)迴圈中 if 語句滿足與不滿足後的 left 和 right 的設置
暫時不討論為什麼這樣子設置
來看終止情況:
終止前的一次: left == right
設 X = left, Y = right (這裡的X和Y是不會變的,因為此時 left == right,所以可以 X == Y)
此時 mid == X (或者Y),結果只有兩種可能,goal對應元素下標為 (1)X對應的 或者 (2)X + 1對應的
前面這句話不理解可以看 while 迴圈中的 if 語句,流程圖如下: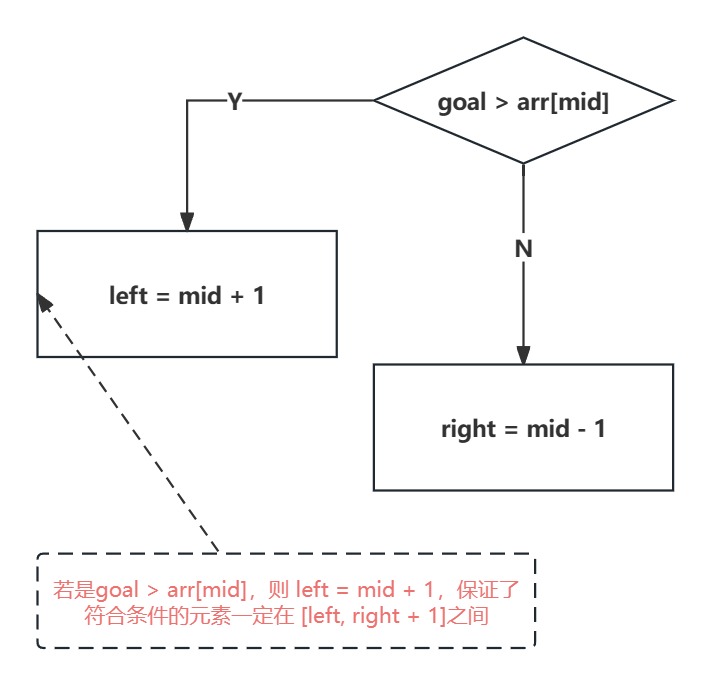
接著我們分析兩種情況:
情況一:X對應的元素是目標值
則此時進入 if 語句,判斷為 N,進入第二個執行語句: right = mid - 1, 則此時 left 不變,結果就是 left, 就是 X
情況二:X + 1對應的元素是目標值
則此時進入 if 語句,判斷為 Y,進入第一個執行語句:left = mid + 1,則此時結果仍然是 left, 就是 X + 1
綜上:cout << l << endl; 就可以得到正確答案!



