C++演算法之旅、05 基礎篇 | 第二章 數據結構

来源:https://www.cnblogs.com/linxiaoxu/archive/2023/09/03/17674897.html
-Advertisement-
Play Games

acwing學習筆記，記錄容易忘記的知識點和難題。數組實現單鏈表、雙鏈表、棧、單調棧、隊列、單調隊列、KMP、字典樹 Trie、並查集、數組實現堆、哈希表（拉鏈法、開放定址法、字元串首碼哈希法）、STL常用容器 ...


常用代碼模板2——數據結構 - AcWing

筆試用數組模擬而不是結構體

使用結構體指針，new Node() 非常慢，創建10萬個節點就超時了，做筆試題不會用這種方式（優化是提前初始化好數組，但這樣跟數組模擬沒區別了，而且代碼量很長）


單鏈表（數組）

使用兩個數組，e存儲val，ne存儲next。空節點next用-1表示

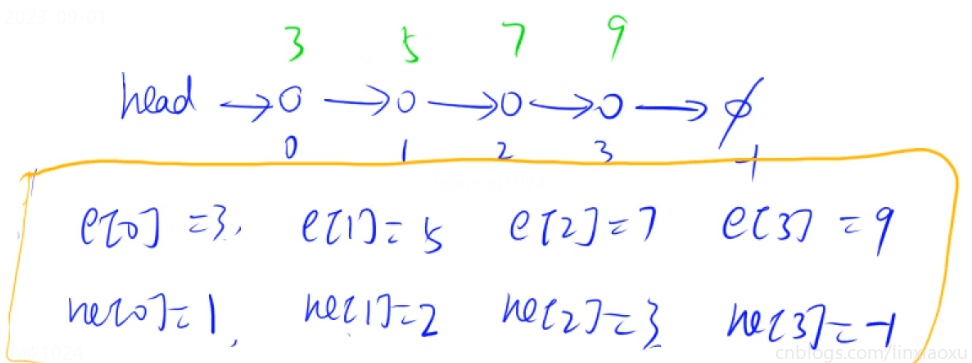
image-20230902031545710

826 ⭐

826. 單鏈表 - AcWing題庫

第1個插入的點下標為0，第5個插入點下標為4，第k個插入點下標為k-1；

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

// head指向頭結點，e[i]表示節點值，ne[i]表示節點next
// idx指向可用空間（當前可以用的最新點下標）
// 演算法題不用考慮浪費的空間
int head, e[N], ne[N], idx;

void init() {
    head = -1;
    idx = 0;
}

// x 插到頭結點後面
void add_to_head(int x) {
    e[idx] = x;
    ne[idx] = head;
    head = idx++;
}

// x 插到下標k的點後面
void add(int k, int x) {
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx++;
}

// 將下標 k 後面點刪掉
void remove(int k) {
    // if (ne[k] == -1) return; 題目保證合法不考慮邊界情況
    ne[k] = ne[ne[k]];
}

int main() {
    int m;
    cin >> m;
    init();
    while (m--) {
        char c;
        int k, x;
        cin >> c;
        if (c == 'H') {
            cin >> x;
            add_to_head(x);
        } else if (c == 'D') {
            cin >> k;
            if (!k)
                head = ne[head];  // 特判刪除頭結點(鏈表第一個有效元素)
            else
                remove(k - 1);
        } else if (c == 'I') {
            cin >> k >> x;
            add(k - 1, x);
        }
    }
    for (int i = head; i != -1; i = ne[i]) {
        cout << e[i] << " ";
    }

    return 0;
}

鄰接表

本質是一堆單鏈表，head[i]->x->x->-1 意思第i個點的鄰邊存起來了

最大用途：存儲圖、樹 （內容在第三章）


雙鏈表（數組）

用於優化某些題，每個節點有兩個指針，一個指向前，一個指向後

需要3個數組，l 數組表示before，r 數組表示next，e 數組表示val，idx指向可用空間

下標0為head，指向頭結點（左端點）；下標1為tail，指向尾結點（右端點）

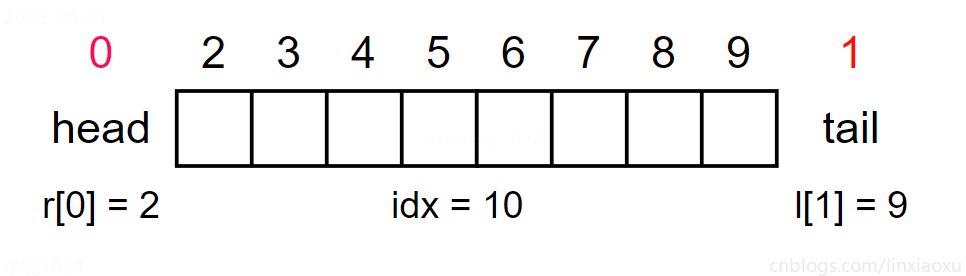
image-20230902040603068

827 ⭐

827. 雙鏈表 - AcWing題庫

因為提前用掉了數組中的兩個，所以第k個插入元素下標是 k - 1 + 2

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int e[N], l[N], r[N], idx;

void init() {
    r[0] = 1;
    l[1] = 0;
    idx = 2;
}

// 在下標k點的右邊插入x（可以轉化成左邊）
void add(int k, int x) {
    e[idx] = x;
    r[idx] = r[k];
    l[idx] = k;
    r[k] = idx;
    l[r[idx]] = idx;
    idx++;
}

// 刪除下標k的點
void remove(int k) {
    l[r[k]] = l[k];
    r[l[k]] = r[k];
}

int main() {
    int m;
    cin >> m;
    init();
    while (m--) {
        string s;
        int k, x;
        cin >> s;
        if (s == "L") {
            cin >> x;
            add(0, x);
        } else if (s == "R") {
            cin >> x;
            add(l[1], x);
        } else if (s == "D") {
            cin >> k;
            remove(k - 1 + 2);
        } else if (s == "IL") {
            cin >> k >> x;
            add(l[k - 1 + 2], x);
        } else if (s == "IR") {
            cin >> k >> x;
            add(k - 1 + 2, x);
        }
    }
    for (int i = r[0]; i != 1; i = r[i]) {
        cout << e[i] << " ";
    }
    return 0;
}

棧

830

828. 模擬棧 - AcWing題庫

先進後出。數據存儲區間為[1,M]，tt為棧頂指針

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int stk[N], tt;

int main() {
    int m;
    cin >> m;
    while (m--) {
        string s;
        int x;
        cin >> s;
        if (s == "push") {
            cin >> x;
            stk[++tt] = x;
        } else if (s == "pop") {
            tt--;
        } else if (s == "empty") {
            if (tt > 0)
                puts("NO");
            else
                puts("YES");
        } else if (s == "query") {
            cout << stk[tt] << endl;
        }
    }
    return 0;
}

3302 ⭐⭐數組

3302. 表達式求值 - AcWing題庫

中綴轉尾碼的重要規則（強行記憶）。轉換與計算可以同步進行（各自需要一個棧）

  • 當前運算符優先順序<=棧頂元素，則棧頂元素依次輸出直到不滿足條件，並當前符號進棧
  • 遇到右括弧，則棧頂元素依次輸出直到左括弧
  • 遍歷完成後彈出棧內剩餘運算符
#include <algorithm>
#include <cstdio>
#include <iostream>
#include <unordered_map>

using namespace std;

const int N = 1e5 + 10;

int op[N], num[N], opt = -1, numt = -1;

unordered_map<char, int> priority;

// 計算尾碼表達式
void eval() {
    auto b = num[numt--];
    auto a = num[numt--];
    auto c = op[opt--];
    int res;
    if (c == '-')
        res = a - b;
    else if (c == '+')
        res = a + b;
    else if (c == '*')
        res = a * b;
    else if (c == '/')
        res = a / b;
    num[++numt] = res;
}

int main() {
    priority = {{'-', 1}, {'+', 1}, {'*', 2}, {'/', 2}};
    string str;
    cin >> str;
    for (int i = 0; i < str.size(); i++) {
        if (isdigit(str[i])) {
            int j = i, res = 0;
            while (isdigit(str[j])) res = res * 10 + str[j++] - '0';
            num[++numt] = res;
            i = j - 1;
        } else if (str[i] == '(')
            op[++opt] = str[i];
        else if (str[i] == ')') {
            while (op[opt] != '(') eval();
            opt--;
        } else {
            while (opt >= 0 && priority[str[i]] <= priority[op[opt]]) eval();
            op[++opt] = str[i];
        }
    }
    while (opt >= 0) eval();
    cout << num[numt];
    return 0;
}

3302 ⭐⭐STL

#include <algorithm>
#include <cstdio>
#include <iostream>
#include <stack>
#include <unordered_map>

using namespace std;

stack<int> num;
stack<char> op;

void eval() {
    auto b = num.top();
    num.pop();
    auto a = num.top();
    num.pop();
    auto c = op.top();
    op.pop();
    int x;
    if (c == '+')
        x = a + b;
    else if (c == '-')
        x = a - b;
    else if (c == '*')
        x = a * b;
    else
        x = a / b;
    num.push(x);
}

int main() {
    unordered_map<char, int> pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
    string str;
    cin >> str;
    for (int i = 0; i < str.size(); i++) {
        auto c = str[i];
        if (isdigit(c)) {
            // 第一類雙指針
            int x = 0, j = i;
            while (j < str.size() && isdigit(str[j]))
                x = x * 10 + str[j++] - '0';
            i = j - 1;  // 考慮i++
            num.push(x);
        } else if (c == '(')
            op.push(c);
        else if (c == ')') {
            while (op.top() != '(') eval();
            op.pop();
        } else {
            while (op.size() && pr[op.top()] >= pr[c]) eval();
            op.push(c);
        }
    }
    while (op.size()) eval();
    cout << num.top() << endl;

    return 0;
}

隊列

829

829. 模擬隊列 - AcWing題庫 隊尾插入，隊頭輸出

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int que[N], st = -1, ed = -1;

int main() {
    int m;
    cin >> m;
    while (m--) {
        string str;
        int x;
        cin >> str;
        if (str == "push") {
            cin >> x;
            que[++ed] = x;
        } else if (str == "pop") {
            st++;
        } else if (str == "empty") {
            if (st == ed)
                puts("YES");
            else
                puts("NO");
        } else if (str == "query") {
            cout << que[st + 1] << endl;
        }
    }

    return 0;
}

單調棧

830 ⭐⭐

830. 單調棧 - AcWing題庫

朴素做法是兩層迴圈。

使用棧，滿足情況：當下標為 i，棧內元素為 \(a_1,a_2...a_i\)

單調棧要求遍曆數組過程中，維護棧，滿足棧底至棧頂元素呈單調性（依次遞增）

  • 棧內 \(a_1\)~\(a_i\) 遞增，此時遍歷至 \(a_{i+1}\)，將小於 \(a_{i+1}\) 的棧內元素刪除，再插入 \(a_{i+1}\)
  • 每個元素一次，出棧一次，\(O(n)\)

scanf 與 cin 速度差了十倍左右，使用 cin.tie(0) 或 ios::sync_with_stdio(false) 加速

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n;
int stk[N], tt;

int main() {
    cin.tie(0);
    // ios::sync_with_stdio(false);
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        while (tt && stk[tt] >= x) tt--;
        if (tt)
            cout << stk[tt] << " ";
        else
            cout << -1 << " ";
        stk[++tt] = x;
    }

    return 0;
}

單調隊列

154 ⭐⭐

154. 滑動視窗 - AcWing題庫

朴素演算法是 \(O(n^2)\)

單調隊列要求滑動視窗每滑動一次時，將視窗內 >= \(a_i\) 的元素從隊尾刪除（類似單調棧），\(a_i\) 入隊，該隊列將保持單調遞增，此時對頭點為最小值。註意隊列里存的是下標

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int a[N], q[N], st = 0, ed = -1;

int main() {
    cin.tie(0);
    int n, k;
    cin >> n >> k;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    for (int i = 0; i < n; i++) {
        // 移動隊頭
        if (st <= ed && i - k + 1 > q[st]) st++;
        // 移動隊尾
        while (st <= ed && a[q[ed]] >= a[i]) ed--;
        // ^ 先插入
        q[++ed] = i;
        // 每次滑動輸出
        if (i >= k - 1) printf("%d ", a[q[st]]);
    }
    cout << endl;
    st = 0;
    ed = -1;
    for (int i = 0; i < n; i++) {
        if (st <= ed && i - k + 1 > q[st]) st++;
        while (st <= ed && a[q[ed]] <= a[i]) ed--;
        q[++ed] = i;
        if (i >= k - 1) printf("%d ", a[q[st]]);
    }

    return 0;
}

KMP

一個人能走多遠不在於他在順境時能走的多快，而在於他在逆境時多久能找到曾經的自己

強烈建議看 胡凡 演算法筆記 P455

KMP字元串 —— 深入淺出 next 數組

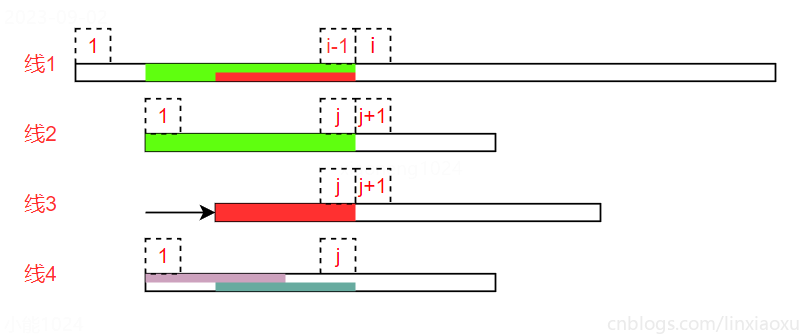
image-20230902122812982

假設下標從1開始。字元串 S[1,N]，子串 P[1,M]，S 指針 i-1，P 指針 j

next[j]

  • 子串中，以 j 為終點的尾碼 與 從1開始的首碼相等的最長長度 x
  • \(P[1,x] = P[j-x+1,j]\)

kmp 建議看演算法筆記

  1. i-1 與 j 對應字元相同；i 與 j+1 對應字元不同。此時需要把紅顏色子串往後移動，為了移動最少需要 next[j]
  2. 讓 j = next[j]，從線2變為線3（線1紅色部分 等於 線3紅色部分）
  3. 繼續匹配 i 與 j+1，若發現不匹配，再 j = next[j] （遞歸進行）
  4. 當 j = m，意味著找到子串，然後 j = next[j] 繼續尋找

時間複雜度計算

  • 生成next數組 \(O(m)\)
  • 字元串每個字元被遍歷一次，\(O(n)\)
  • j++ 最多 n 次，最多減 n 次，\(O(n)\)

831 ⭐⭐⭐

831. KMP字元串 - AcWing題庫

next 在某些頭文件里有定義，最好換個變數名；另外KMP演算法還可以進一步優化，以下是優化後的演算法

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;
const int M = 1e6 + 10;
int next_val[N];

int main() {
    int n, m;
    char p[N], s[M];
    cin >> n >> p + 1 >> m >> s + 1;
    // ^ 生成 next_val 數組
    for (int i = 2, j = 0; i <= n; i++) {
        while (j && p[i] != p[j + 1]) j = next_val[j];
        if (p[i] == p[j + 1]) j++;
        // ^ 繼續優化，選擇回退的最佳位置
        if (j && p[i + 1] == p[j + 1]) {
            next_val[i] = next_val[j];
        } else
            next_val[i] = j;
    }
    // for (int i = 1; i <= n; i++) {
    //     cout << next_val[i] << endl;
    // }
    // ^ KMP 匹配過程
    for (int i = 1, j = 0; i <= m; i++) {
        while (j && p[j + 1] != s[i]) j = next_val[j];
        if (p[j + 1] == s[i]) j++;
        if (j == n) {
            cout << i - n << " ";
            j = next_val[j];
        }
    }
    return 0;
}

字典樹 Trie

用於高效存儲和查找字元串集合的數據結構

835

835. Trie字元串統計 - AcWing題庫

son[N][26] 存的是每個節點所有的兒子是什麼，cnt[N] 存的是單詞的數量，idx與數組模擬單鏈表裡的idx相同

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int son[N][26], cnt[N], idx;  // ^ 下標是0的點，既是根節點又是空節點

void insert(char str[]) {
    int p = 0;
    for (int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++idx;
        p = son[p][u];
    }
    cnt[p]++;
}

int query(char str[]) {
    int p = 0;
    for (int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

int main() {
    cin.tie(0);
    int n;
    cin >> n;
    while (n--) {
        char a, b[N];
        cin >> a >> b;
        if (a == 'I')
            insert(b);
        else
            cout << query(b) << endl;
    }
    return 0;
}

143 ⭐⭐

143. 最大異或對 - AcWing題庫

朴素演算法是兩層迴圈並滿足 j<i（避免重覆， \(C^2_n = n*(n-1)/2\) ）；時間複雜度 \(O(n^2)\) ，題目給的 n 是 1e5，則 1e10 超時

可以使用 trie tree 優化，每插入一個元素 x，在字典樹中查找滿足與該元素異或最大值的元素（儘可能反著取，每次查找只要遍歷31位），時間複雜度 \(O(n)\)

可以先插入再遍歷（少個判斷），第一個插入的元素與自身異或為 0

每個節點個數長31，最多1e5個，那麼idx最大可以到 31 * 1e5

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10, M = 31 * N;

int son[M][2], idx;

void insert(int x) {
    int p = 0;
    for (int i = 30; i >= 0; i--) {
        int bit = x >> i & 1;
        if (!son[p][bit]) son[p][bit] = ++idx;
        p = son[p][bit];
    }
}

int query(int x) {
    int res = 0, p = 0;
    for (int i = 30; i >= 0; i--) {
        int bit = x >> i & 1;
        if (son[p][!bit]) {
            bit = !bit;
        }
        p = son[p][bit];
        res = (res << 1) + bit;
    }
    return res;
}

int main() {
    int n;
    cin >> n;
    int m = 0;
    while (n--) {
        int x;
        cin >> x;
        insert(x);
        m = max(x ^ query(x), m);
    }
    cout << m;

    return 0;
}

並查集

操作

  • 將兩個集合合併
  • 詢問兩個元素是否在一個集合當中

朴素演算法下，合併兩個集合需要執行\(O(n+m)\)次；並查集可以近乎\(O(1)\)合併兩個集合

基本原理

  • 用樹的形式維護所有集合；根節點是集合編號
  • 每個節點存儲父節點，p[x] 表示x的父節點

如何判斷樹根

  • if (p[x] == x) ，根節點的父節點是它本身

如何求x的集合編號

  • while(p[x] != x) x = p[x]
  • 路徑壓縮⭐ ：往上走找到根節點把路徑所有點都指向跟節點

如何合併兩個集合 ⭐ 記住模板

  • p[x] = y，將一顆樹根節點插到另一棵樹的某個位置
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

如何維護集合元素個數（攜帶額外信息）

  • 見837題

836 ⭐

836. 合併集合 - AcWing題庫

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int p[N];

// ^ 返回x祖宗節點 + 路徑壓縮
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    cin.tie(0);
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) p[i] = i;

    while (m--) {
        char op;
        int a, b;
        cin >> op >> a >> b;
        if (op == 'M') {
            p[find(a)] = find(b);
        } else {
            if (find(a) == find(b))
                puts("Yes");
            else
                puts("No");
        }
    }
    return 0;
}

837 ⭐⭐

837. 連通塊中點的數量 - AcWing題庫

保證根節點的nums有意義

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int p[N], nums[N];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    cin.tie(0);
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        p[i] = i;
        nums[i] = 1;
    }
    while (m--) {
        string op;
        int a, b;
        cin >> op;
        if (op == "C") {
            cin >> a >> b;
            // ^ 特判
            if (find(a) == find(b)) continue;
            // ^ 先算元素個數再合併
            nums[find(b)] += nums[find(a)];
            p[find(a)] = find(b);
        } else if (op == "Q1") {
            cin >> a >> b;
            if (find(a) == find(b))
                puts("Yes");
            else
                puts("No");
        } else if (op == "Q2") {
            cin >> a;
            cout << nums[find(a)] << endl;
        }
    }
    return 0;
}

240 ⭐⭐⭐

240. 食物鏈 - AcWing題庫

確定每個動物跟領袖（n對1）的關係，而不是動物跟動物（n對n）的關係

維護每個節點與根節點的距離（x吃y，y到x距離是1），然後 % 3 判斷類型。初始化每個節點都是0，各自一類。

  • 餘1：可以吃根節點
  • 餘2：可以被根節點吃
  • 餘0：與根節點是同類
#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int p[N], d[N];

int find(int x) {
    if (p[x] != x) {
        // 遞歸處理所有祖宗節點，並更新到根的距離
        int t = find(p[x]);
        // d[x] 等於 x到父的距離 + 父到根的距離（遞歸處理完了）
        d[x] += d[p[x]];
        // x 的父修改為根節點，路徑優化
        p[x] = t;

        // // 記錄舊的父
        // int u = p[x];
        // // 路徑壓縮，新父根節點
        // p[x] = find(p[x]);
        // // x到根的距離等於x到舊父距離加上舊父到根的距離
        // d[x] += d[u];
    }
    return p[x];
}

int main() {
    cin.tie(0);
    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; i++) p[i] = i;

    int count = 0;
    while (k--) {
        char t;
        int x, y;
        cin >> t >> x >> y;
        if (x > n || y > n) {
            count++;
        } else {
            int px = find(x), py = find(y);
            if (t == '1') {
                if (px == py && (d[x] - d[y]) % 3 != 0)
                    count++;
                else if (px != py) {
                    p[px] = py;
                    d[px] = d[y] - d[x];  // IMPORTANT
                }
            } else {
                if (x == y || px == py && (d[x] - d[y] - 1) % 3 != 0) {
                    count++;
                } else if (px != py) {
                    p[px] = py;
                    d[px] = d[y] + 1 - d[x];
                }
            }
        }
    }
    cout << count << endl;

    return 0;
}

堆

小根堆

每個點 <= 左右兒子，根節點就是樹的最小值 。

完全二叉樹用一維數組存：x 的左兒子 2x，x 的右兒子 2x+1；下標從1開始


兩個操作 ⭐

  • down(x) 往下調整 （x是坐標 1 ~ size） \(O(log_2n)\)
    • 每次找{ x，x左子，x右子 }的最小值，進行交換
  • up(x) 往上調整 \(O(log_2n)\)
    • 每次找{ x，x父 }的最小值，進行交換

堆的功能

  • 插入一個數 \(O(log_2n)\)
    • heap[++size] = x 然後不斷往上移 up(size)
  • 求集合當中的最小值 \(O(1)\)
    • heap[1]
  • 刪除最小值 \(O(log_2n)\)
    • heap[1] = heap[size--] 堆最後一個元素覆蓋堆頂元素，然後 down(1)
    • 因為刪除頭結點非常困難，刪除尾結點很easy
  • 刪除任意一個元素（STL沒直接實現，優先隊列） \(O(log_2n)\)
    • heap[k] = heap[size--] 有三種情況，可直接 down(k) 再 up(k)，只會執行一個
  • 修改任意一個元素（STL沒直接實現，優先隊列） \(O(log_2n)\)
    • heap[k] = x 再 down(k) 、up(k)

838 ⭐

838. 堆排序 - AcWing題庫

一個一個往裡插是 \(O(nlog_2n)\) 。可以採用 \(O(n)\) 的方式，先全部讀入，除最後一層外反著down操作（倒第2層，倒第3層...第1層）（可用數列推導出，每個節點down的次數總和 < n）（記憶）

    for (int i = n / 2; i; i--) {
        down(i);
    }


#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], idx;

void down(int u) {
    int t = u;
    if (u * 2 <= idx && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= idx && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t) {
        swap(h[t], h[u]);
        down(t);
    }
}

int main() {
    cin.tie(0);
    cin >> n >> m;
    int x;
    for (int i = 1; i <= n; i++) {
        cin >> h[i];
    }
    idx = n;

    for (int i = n / 2; i; i--) {
        down(i);
    }

    while (m--) {
        cout << h[1] << " ";
        h[1] = h[idx--];
        down(1);
    }

    return 0;
}

839 ⭐⭐

839. 模擬堆 - AcWing題庫

存儲映射：ph 存第k個插入的點在堆里的下標，hp 存堆里點的坐標是第k個插入的，兩者互為相反關係。

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int h[N], hp[N], ph[N], idx;

void new_swap(int a, int b) {
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void up(int x) {
    while (x / 2 && h[x / 2] > h[x]) {
        new_swap(x / 2, x);
        x /= 2;
    }
}

void down(int x) {
    int t = x;
    if (2 * x <= idx && h[2 * x] < h[t]) t = 2 * x;
    if (2 * x + 1 <= idx && h[2 * x + 1] < h[t]) t = 2 * x + 1;
    if (t != x) {
        new_swap(x, t);
        down(t);
    }
}

int main() {
    cin.tie(0);
    int n;
    cin >> n;
    int count = 0;
    while (n--) {
        string s;
        int k, x;
        cin >> s;
        if (s == "I") {
            cin >> x;
            idx++;
            count++;
            h[idx] = x;
            hp[idx] = count;
            ph[count] = idx;
            up(idx);
        } else if (s == "PM") {
            cout << h[1] << endl;
        } else if (s == "DM") {
            // ^ h[1] = h[idx--];  // 這樣只交換點,沒交換ph hp
            new_swap(1, idx--);
            down(1);
        } else if (s == "D") {
            cin >> k;
            // ^ h[ph[k]] = h[idx--]; // 這樣只交換點,沒交換ph hp
            k = ph[k];  // 獲取第k個插入的數在堆中的坐標
            new_swap(k, idx--);
            down(k), up(k);  // 只會執行其中一個
        } else if (s == "C") {
            cin >> k >> x;
            k = ph[k];
            h[k] = x;
            down(k), up(k);
        }
    }

    return 0;
}

哈希表

情景

  • 把 1e5 個值域 -1e9~1e9 的數（值域大，個數少）映射到 1e5 的範圍的哈希函數
  • \(h(x) \in (0,1e5) = x\ mod\ 1e5\) 模數一般要取質數，離2的整數冪儘可能遠
  • 發生衝突：兩個不同值域的數映射成了同一個數

存儲結構-解決衝突的方式 ⭐

演算法題99%一般只有添加、查找，若要實現刪除不會真刪掉，開一個bool數組標記刪除

  • 開放定址法（常用）
    • 開一個一維數組，範圍是題目數據範圍的2~3倍，即 2e5 ~ 3e5 區間的質數，該數組存儲實際的 x 值
    • 計算哈希值，如果哈希值已被占用，則移動到下一個位置，從前往後找
    • h(11) = 3 在 數組[3] 存入 11，h(4) = 3 在數組[4] 存入 4
    • 與拉鏈法不同，查詢函數返回 x 所在的位置，如果 x 不存在返回應該存儲的位置
    • 需要約定一個標誌，不在 x 的值域範圍內，表示當前位置為空，如 0x3f3f3f3f
  • 拉鏈法
    • 開一個一維數組 \([0,大於1e5的最小質數]\) 存儲所有哈希值對應的鏈表
    • h(11) = 3 在 數組[3] 開一條鏈，插入 11
    • 若 h(4) = 3 在 數組[3] 已開的鏈插入 4
    • 期望情況下，每條鏈長度 1，時間複雜度 \(O(1)\)

字元串哈希-字元串首碼哈希法（特殊）

應用：可以快速判斷一個字元串某兩段是否相同。KMP望而卻步（KMP擅長迴圈節），極困難題可用這種方法

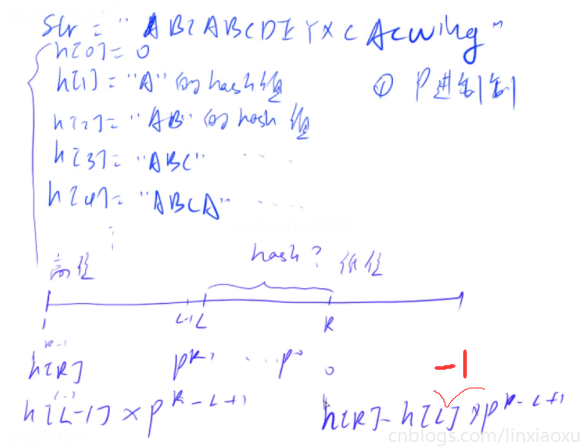
  • 先預處理所有首碼的哈希，h[0] = 0, h[1] = "A" 的hash，h[2] = "AB" 的hash...

    • 把字元串看成 P 進位的數，然後模 Q
    image-20230903101708987

  • **某個字元不能映射成 0，否則 AA 跟 A 兩個哈希都是 0 **

  • 該哈希法假定人品足夠好，不考慮衝突

  • 經驗值：當 p = 131 或 13331，Q 取 \(2^{64}\) (用 unsinged long long可以不取模，溢出相當於取模)

⭐ 我們可以利用首碼哈希算出任意子段的哈希值

  • 預處理首碼 h(i) = h(i-1) * p + str[i]

image-20230903110147424


與整數離散化的區別

整數離散化需要保序，而且不會發生衝突，每一個元素都有唯一確定的位置（1 ~ n）

840 ⭐拉鏈法

840. 模擬散列表 - AcWing題庫

h 數組維護 N 條鏈，空節點表示-1，e 數組與 ne 數組維護鏈上的每一個節點，idx為每個節點分配唯一標識符；插入操作從鏈表頭結點插入

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 1e5 + 3;  // 質數

int h[N], e[N], ne[N], idx;

void insert(int x) {
    // 第一次模餘數可能是負數，第二次模餘數絕對是正數
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx++;
}

bool find(int x) {
    int k = (x % N + N) % N;
    for (int i = h[k]; i != -1; i = ne[i])
        if (e[i] == x) return true;

    return false;
}

int main() {
    cin.tie(0);
    memset(h, -1, sizeof h);
    int n;
    cin >> n;
    while (n--) {
        string s;
        int x;
        cin >> s >> x;
        if (s == "I")
            insert(x);
        else {
            if (find(x))
                puts("Yes");
            else
                puts("No");
        }
    }
    return 0;
}

840 ⭐開放定址法

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 2e5 + 3, null = 0x3f3f3f3f;  // 質數

int h[N];

int find(int x) {
    int k = (x % N + N) % N;
    while (h[k] != null && h[k] != x) {
        k++;
        if (k == N) k = 0;  // 查到數組最後從開頭找
    }
    return k;
}

int main() {
    cin.tie(0);
    memset(h, 0x3f, sizeof h);
    int n;
    cin >> n;
    while (n--) {
        string s;
        int x;
        cin >> s >> x;
        int k = find(x);
        if (s == "I")
            h[k] = x;
        else {
            if (h[k] != null)
                puts("Yes");
            else
                puts("No");
        }
    }
    return 0;
}

841 ⭐⭐ 字元串哈希

841. 字元串哈希 - AcWing題庫

如下的朴素演算法會超時

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

int main() {
    cin.tie(0);
    string s;
    int n, m, l1, l2, r1, r2;
    cin >> n >> m >> s;
    while (m--) {
        cin >> l1 >> r1 >> l2 >> r2;
        l1 -= 1, l2 -= 1, r1 -= 1, r2 -= 1;
        if (s.substr(l1, r1 - l1 + 1) == s.substr(l2, r2 - l2 + 1))
            puts("Yes");
        else
            puts("No");
    }

    return 0;
}

p 數組提前存儲預處理的 p 次方的值，減少計算量

#include <algorithm>
#include <cstdio>
#include <iostream>

using namespace std;

typedef unsigned long long ULL;

const int N = 1e5, P = 131;

int n, m;
char str[N];
ULL h[N], p[N];

ULL get(int l, int r) { return h[r] - h[l - 1] * p[r - l + 1]; }

int main() {
    cin.tie(0);
    cin >> n >> m >> str + 1;
    p[0] = 1;
    for (int i = 1; i <= n; i++) {
        p[i] = p[i - 1] * P;
        h[i] = h[i - 1] * P + str[i];
    }

    while (m--) {
        int l1, r1, l2, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        if (get(l1, r1) == get(l2, r2))
            puts("Yes");
        else
            puts("No");
    }
    return 0;
}

STL

size()、empty() 所有容器都有，時間複雜度 \(O(1)\)

clear() 並不是所有容器都有，隊列、優先隊列、棧；範圍遍歷可以遍歷所有容器

⭐ 系統為某一個程式分配空間時，所需的時間與空間大小無關，與申請次數有關


vector

變長數組，倍增，支持比較運算（字典序（4個3小於3個4））。有erase但用得不多

插入操作\(O(1)\)：插入1e6次，申請空間的次數 \(log_21e6\) ，拷貝的次數均攤是 1 （數組大小從1到1e6，總共拷貝次數是1e6（1+2+4+8+...））

#include <iostream>
#include <vector>

using namespace std;

int main() {
    // ^ 定義一個長度為10的vector，每個數都是3
    vector<int> a(10, 3);
    vector<int> b[10];

    a.push_back(1);

    cout << a.size() << endl;
    cout << a.empty() << endl;
    a.clear();
    cout << a.front() << endl;
    cout << a.back() << endl;
    // a.begin(); // ^ 返回的是迭代器（指針），需要解引用
    // a.end();
    return 0;
}

pair

二元組，支持比較運算（字典序）。適用於某種東西有兩個屬性，也可以存儲三個屬性，任意嵌套

相比結構體：pair 幫我們實現了結構體，並實現了比較函數，省了點代碼

#include <iostream>

using namespace std;

int main() {
    pair<int, pair<int, string>> a;
    pair<int, string> p;
    p = {20, "abc"};
    p.first;
    p.second;
    return 0;
}

string

字元串，substr(起始位置，長度)、c_str()

#include <cstdio>
#include <iostream>

using namespace std;

int main() {
    string a = "yxc";
    a += "def";
    a += "c";
    // 從哪開始，返回多長（可省略）
    cout << a.substr(1, 2) << endl;
    printf("%s\n", a.c_str());
    return 0;
}

queue

隊列，push()、front()、pop()，沒有 clear()

int main() {
    queue<int> q;
    // ^ 沒有clear的清空方法
    q = queue<int>();
    return 0;
}

deque

雙端隊列，支持隨機訪問 []。相當於加強版 vector。效率較低，不常用

front、back、push_back、pop_back、push_front、pop_front


priority_queue

優先隊列，預設是大根堆。push()、top()、pop()。頭文件queue

int main() {
    priority_queue<int> heap;
    // ^ 定義小根堆
    // 方式 1 每次插入負數
    // heap.push(-x);
    // 方式 2 多加兩個參數
    priority_queue<int, vector<int>, greater<int>> heap;
    return 0;
}

stack

棧，push()、top()、pop()；與隊列用法類似


set、map、multiset、multimap

基於平衡二叉樹（紅黑樹），動態維護有序序列。begin、end支持++、--操作，返回前驅後繼（有序序列的前一個數或後一個數）。增刪改查大部分 \(O(log_2n)\)

#include <iostream>
#include <set>

using namespace std;

int main() {
    set<int> s;
    multiset<int> ms;
    s.insert(1);
    // 找不到返回 end 迭代器
    s.find(1);
    // 返回某個數的個數
    s.count(1);
    // 刪除所有等於這個數的節點 O(k + logn) k是x的個數
    ms.erase(1);
    // 刪除這個迭代器
    ms.erase(ms.find(1));
    // 大於等於 x 的最小的數的迭代器，不存在返回end
    s.lower_bound(0);
    // 大於 x 的最小的數的迭代器，不存在返回end
    s.upper_bound(0);
    return 0;
}


#include <iostream>
#include <map>

using namespace std;

int main() {
    map<string, int> a;
    a.insert({"abc", 123});
    // erase 跟 set 一樣
    // 可以像數組一樣用 map，時間複雜度 O(logn)
    count << a["abc"] << endl;
    // 也支持 lower_bound、upper_bound
    return 0;
}

unordered_

沒有順序，基於哈希表實現。與上面類似。但增刪改查時間複雜度是 \(O(1)\)

不支持 lower_bound、upper_bound；不支持迭代器 ++ --


bitset

壓位。C++里bool是1位元組，如果要開1024個bool數組需要1024個位元組，如果用壓位，只需要128B

1e4 * 1e4 布爾矩陣，需要 1e8B，約100MB，題目給的 64MB，用壓位可以縮小到12MB

int main() {
    bitset<10000> s;
    // ~ & | ^ >> << == != []
    // count() 返回有多少個 1
    // any() 判斷是否至少有1個 1
    // none() 判斷是否全為 0
    // set() 把所有位置1
    // set(k,v) 將第k位變成v
    // reset() 把所有位變成0
    // flip() 等價於 ~
    // flip(k) 把第k位取反
    return 0;
}

您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 領域建模的體系化思維與6種方法論
    本文希望能夠通過總結過去自己對領域建模的一點粗淺經驗給需要的同學能有些許啟發，少走彎路。 背景 軟體工程師做的核心事情就是對現實世界的問題進行抽象然後用電腦的語言對其進行重新刻畫，在通過信息化來提高生產力。而這其中一個關鍵環節就是如何對問題域進行建模，在過去的工作中經常遇到一個問題是前期因為業務比 ...
  • c++單例模式總結
    分類 懶漢式：實例對象在第一次被使用時才進行初始化。 餓漢式：實例在定義時就被初始化。 特點 1、構造函數和析構函數私有化，不允許外部創建實例對象。 2、拷貝構造函數和複製運算符重載被delete，不允許產生新的實例。 3、內部定義一個私有的靜態數據成員，該成員為本類的實例化對象。 4、提供公有靜態 ...
  • 10分鐘從源碼級別搞懂AQS（AbstractQueuedSynchronizer）
    10分鐘從源碼級別搞懂AQS（AbstractQueuedSynchronizer） ### 前言 上篇文章[15000字、6個代碼案例、5個原理圖讓你徹底搞懂Synchronized](https://juejin.cn/post/7272015112819556412)有說到synchroniz ...
  • Nacos 註冊中心的設計原理：讓你的應用輕鬆實現高效註冊與發現！
    當應用開始脫離單機運行和訪問時，服務發現就誕生了。目前的網路架構是每個主機都有⼀個獨立的 IP 地址，服務發現基本都是通過某種方式獲取到服務所部署的 IP 地址。 DNS 協議是最早將⼀個網路名稱翻譯為網路 IP 的協議，在最初的架構選型中，DNS+LVS+Nginx 基本滿足所有 RESTful ...
  • Go 條件
    **條件語句**用於根據不同的條件執行不同的操作。 Go中的條件可以是真或假。 Go支持數學中常見的比較運算符： 小於 大於等於 >= 等於 == 不等於 != 此外，Go還支持常見的邏輯運算符： 邏輯與 && 邏輯或 || 邏輯非 ! 您可以使用這些運算符或它們的組合來創建不同決策的條件。 **示 ...
  • 電商類面試問題--01Elasticsearch與Mysql數據同步問題
    在實現基於關鍵字的搜索時，首先需要確保MySQL資料庫和ES庫中的數據是同步的。為瞭解決這個問題，可以考慮兩層方案。 1. 全量同步：全量同步是在服務初始化階段將MySQL中的數據與ES庫中的數據進行全量同步。可以在服務啟動時，對ES庫進行全量數據同步操作，以確保數據的一致性。而在停止服務時，可以清 ...
  • LeetCode952三部曲之二：小幅度優化(137ms -＞ 122ms，超39% -＞ 超51%)
    ### 歡迎訪問我的GitHub > 這裡分類和彙總了欣宸的全部原創(含配套源碼)：[https://github.com/zq2599/blog_demos](https://github.com/zq2599/blog_demos) ### 本篇概覽 - 本文是《LeetCode952三部曲》系 ...
  • MIPS寄存器堆
    # 實驗目的 - 熟悉並掌握 MIPS 電腦中寄存器堆的原理和設計方法 - 理解源操作數/目的操作數的概念 # 實驗環境 * Vivado 集成開發環境 # MIPS寄存器 ![](https://pic.imgdb.cn/item/64f40fab661c6c8e5400bf9a.jpg) * ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類