什麼是敏感性分析 敏感性分析(sensitivity analysis)是指從定量分析的角度研究有關因素髮生某種變化對某一個或一組關鍵指標影響程度的一種不確定分析技術。每個輸入的靈敏度用某個數值表示即敏感性指數(sensitivity index) 敏感性指數包括以下幾種: 一階指數:度量單個模型輸 ...
什麼是敏感性分析
敏感性分析(sensitivity analysis)是指從定量分析的角度研究有關因素髮生某種變化對某一個或一組關鍵指標影響程度的一種不確定分析技術。每個輸入的靈敏度用某個數值表示即敏感性指數(sensitivity index) 敏感性指數包括以下幾種:- 一階指數:度量單個模型輸入對輸出方差的貢獻
- 二階指數:度量兩個模型輸入的相互作用對輸出方差的貢獻
- 總階指數:度量模型輸入對輸出方差的貢獻,包括一階及更高階
什麼是SALib
SALib是一個基於python進行敏感性分析的開源庫,SALib提供一個解耦的工作流,意味著它不直接與數學或計算模型交互,SALib 負責使用其中一個採樣函數(sample functions)生成模型輸入,並使用其中一個分析函數(analyze functions)計算模型輸出的靈敏度指數。使用 SALib 進行敏感性分析遵循四個步驟:
- 確定模型輸入(參數)及採樣範圍
- 運行採樣函數生成模型輸入
- 使用生成的輸入評估模型,保存模型輸出
- 基於模型輸出運行分析函數計算敏感性指數SALib提供了幾種靈敏度分析函數,如Sobol,Morris和FAST。有許多因素決定了哪種方法適用於特定應用。但是無論選擇哪種方法,都只需要用到兩種函數:sample,analyze
案例1
對Ishigami function進行Sobol敏感性分析,因為Ishigami函數表現出很強的非線性和非單調性,所以常用來測試不確定性和敏感性分析方法

1.導入庫
SALib的採樣和分析存儲在不同的模塊中,例如導入saltelli採樣函數和sobol分析函數,使用Ishigami作為測試函數,numpy用於存儲模型輸入和輸出
from SALib.sample import saltelli from SALib.analyze import sobol from SALib.test_functions import Ishigami import numpy as np
2.定義模型輸入
problem = { 'num_vars':3, 'names':['x1','x2','x3'], 'bounds':[[-3.14159265359, 3.14159265359], [-3.14159265359, 3.14159265359], [-3.14159265359, 3.14159265359]] }
3.生成樣本
使用saltelli生成樣本
param_values = saltelli.sample(problem,1024)
param_values是一個numpy矩陣,其大小為(8192, 3),saltelli會生成N*(2D+2)個樣本,其中N=1024(傳入參數),D=3(模型輸入數量)。參數calc_second_order=False表示不包括二階指數,採樣數變為N*(D+2)
param_values
array([[-3.13238877, -0.77619428, -0.32827189], [-0.08283496, -0.77619428, -0.32827189], [-3.13238877, 0.3589515 , -0.32827189], ..., [-0.93572828, 0.80073797, 0.99095159], [-0.93572828, 0.81914574, 2.70901007], [-0.93572828, 0.81914574, 0.99095159]])
param_values.shape
(8192, 3)
4.運行模型
SALib不直接參与數學或計算模型的評估,如果模型是用python書寫,可以直接迴圈遍歷每個樣本輸入和評估模型
Y = np.zeros([param_values.shape[0]]) for i,X in enumerate(param_values): Y[i] = evaluate_model(X)
如果模型不是python書寫,可以保存模型的輸入輸出
np.savetext('param_values.txt',param_values) Y = np.loadtxt('outputs.txt',float)
本例中使用Ishigami函數評估樣本數據
Y = Ishigami.evaluate(param_values)
Y
array([ 3.426362 , 3.3527401 , 0.85463176, ..., 2.72470174,
-1.40463805, 2.85339365])
5.分析
在得到模型的輸出後可以計算敏感性指數。本例中使用sobol.analyze,會計算一階,二階和總階指數
Si = sobol.analyze(problem,Y,print_to_console=True)
ST ST_conf x1 0.555860 0.080045 x2 0.441898 0.034177 x3 0.244675 0.025569 S1 S1_conf x1 0.316832 0.068707 x2 0.443763 0.046636 x3 0.012203 0.064176 S2 S2_con (x1, x2) 0.009254 0.093058 (x1, x3) 0.238172 0.111655 (x2, x3) -0.004888 0.066105
Si是一個字典,關鍵詞有"S1", “S2”, “ST”, “S1_conf”, “S2_conf”, and “ST_conf”。_conf存儲相應的置信區間,置信水平在95%。可以使用print_to_console=True 列印所有的指數,或者直接取鍵值。
Si
{'S1': array([0.31683154, 0.44376306, 0.01220312]),
'S1_conf': array([0.06314249, 0.05230396, 0.05764901]),
'ST': array([0.55586009, 0.44189807, 0.24467539]),
'ST_conf': array([0.08582851, 0.04184123, 0.02424759]),
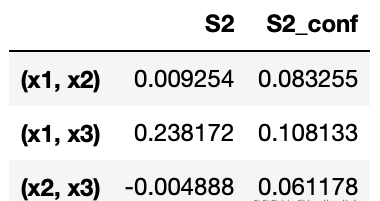
'S2': array([[ nan, 0.00925429, 0.23817211],
[ nan, nan, -0.0048877 ],
[ nan, nan, nan]]),
'S2_conf': array([[ nan, 0.08325501, 0.10813299],
[ nan, nan, 0.06117807],
[ nan, nan, nan]])}
print(Si['S1'])
[0.31683154 0.44376306 0.01220312]
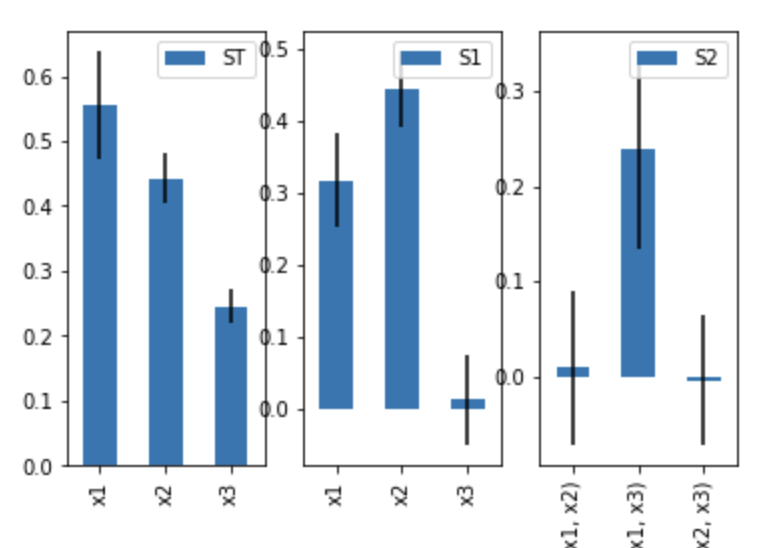
可以看出x1和x2表現出了一階靈敏性,但是x3沒有一階效應
如果總階指數基本上比一階指數大,則可能發生了高階交互作用,可以查看二階指數
print('x1-x2:',Si['S2'][0,1]) print('x1-x3:',Si['S2'][0,2]) print('x2-x3:',Si['S2'][1,2])
x1-x2: 0.00925429303490799 x1-x3: 0.2381721095685646 x2-x3: -0.004887704633467273
x1和x3之間有較強的交互,有時也會出現計算誤差,如x2-x3指數為負,隨著樣本的增加,這些誤差會縮小。
輸出也可以變成Pandas DataFrame從而進行其它分析
total_si,first_si,second_si = Si.to_df()
second_si
6.繪圖
為了方便起見,SALib提供了基本的繪圖功能
Si.plot()
案例2
當你想要分析的模型依賴於不是敏感性分析的參數(如位置和時間),則可以單獨對每個時間/位置進行分析。以拋物線函數為例
參數a,b將接受敏感性分析,但是x不會
首先導入需要的庫
import numpy as np import matplotlib.pyplot as plt from SALib.sample import saltelli from SALib.analyze import sobol
定義拋物線函數
def parabola(x,a,b): return a + b*x**2
字典描述只包含a,b的問題
problem = { 'num_vars':2, 'names':['a','b'], 'bounds':[[0,1]]*2 }
採樣,評估,分析。此例中選舉100個x的取值,針對需要進行敏感性分析的a,b的每個樣本(共384個)計算y值,因此y的大小為(384, 100)
param_values = saltelli.sample(problem,2**6) print(param_values.shape)
(384, 2)
x = np.linspace(-1,1,100) y = np.array([parabola(x,*params) for params in param_values])
print(x.shape) print(y.shape)
(100,)
(384, 100)
print(y)
[[0.421875 0.40593913 0.39032847 ... 0.39032847 0.40593913 0.421875 ] [1.21875 1.20281413 1.18720347 ... 1.18720347 1.20281413 1.21875 ] [0.859375 0.82594091 0.79318915 ... 0.79318915 0.82594091 0.859375 ] ... [0.640625 0.61531508 0.59052169 ... 0.59052169 0.61531508 0.640625 ] [1.21875 1.19219021 1.16617246 ... 1.16617246 1.19219021 1.21875 ] [1.1875 1.16219008 1.13739669 ... 1.13739669 1.16219008 1.1875 ]]
此例中的敏感性指數是一個長度為100的列表,每個元素是一個如上例中的字典
sobol_indices = [sobol.analyze(problem,Y) for Y in y.T] sobol_indices[0]
{'S1': array([0.49526584, 0.49526584]),
'S1_conf': array([0.17061222, 0.21853518]),
'ST': array([0.49745084, 0.49672251]),
'ST_conf': array([0.15376801, 0.16325137]),
'S2': array([[ nan, 0.00436999],
[ nan, nan]]),
'S2_conf': array([[ nan, 0.39998034],
[ nan, nan]])}
len(sobol_indices)
100
接下來單獨分析每個x對應的指數,提取一階指數繪圖
# 提取100個a,b一階指數 S1s = np.array([s['S1'] for s in sobol_indices]) fig = plt.figure(figsize=(10,6),constrained_layout = True) gs = fig.add_gridspec(2,2) ax0 = fig.add_subplot(gs[:,0]) ax1 = fig.add_subplot(gs[0,1]) ax2 = fig.add_subplot(gs[1,1]) for i,ax in enumerate([ax1,ax2]): ax.plot(x,S1s[:,i], label=r'S1$_\mathregular{{{}}}$'.format(problem["names"][i]), color = 'black') ax.set_xlabel('x') ax.set_ylabel('First-order Sobol index') ax.set_ylim(0,1.04) ax.yaxis.set_label_position("right") ax.yaxis.tick_right() ax.legend(loc='upper right') ax0.plot(x,np.mean(y,axis=0),label="Mean", color='black') prediction_interval = 95 ax0.fill_between(x, np.percentile(y, 50 - prediction_interval/2., axis=0), np.percentile(y, 50 + prediction_interval/2., axis=0), alpha=0.5, color='black', label=f"{prediction_interval} % prediction interval") ax0.set_xlabel("x") ax0.set_ylabel("y") ax0.legend(title=r"$y=a+b\cdot x^2$", loc='upper center')._legend_box.align = "left" plt.show()
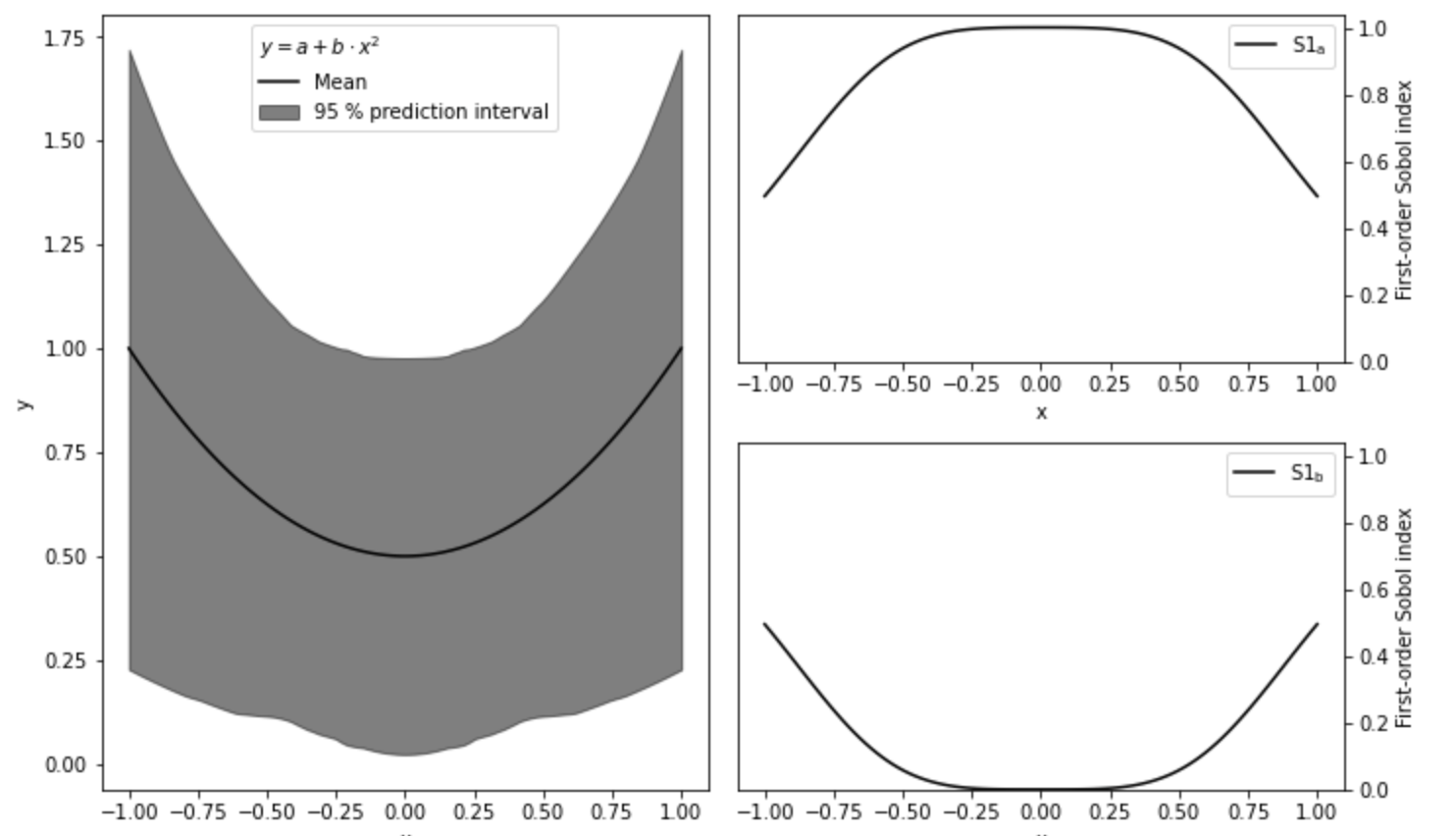
左圖為每個x對應不同a,b取值下y的均值以及95%置信區間,右圖為參數a,b的一階指數。由圖可知,在x=0時,y完全由參數a決定,參數b由於x而消失,x的絕對值越大,參數b對變化貢獻越大,參數a相應越小


