摘要：本文詳細介紹Kmeans聚類演算法的原理和程式實現。首先介紹利用該演算法的原理及理解，詳細介紹基於MATLAB設計一個自定義的Kmeans函數過程，然後利用該函數對UCI的數據集進行聚類以測試聚類結果。後續章節將介紹的主要部分有：

• Kmeans演算法的原理及理解
• 編程實現
• 聚類結果評價
• 類簇中心點的選取

點擊下載：本文Kmeans演算法M函數及測試完整文件

1. 前言

作為無監督聚類演算法中的代表——K均值聚類（Kmeans）演算法，該演算法的主要作用是將相似的樣本自動歸到一個類別中。所謂的監督演算法，就是輸入樣本沒有對應的輸出或標簽。聚類（clustering）試圖將數據集中的樣本劃分為若幹個通常是不相交的子集，每個子集稱為一個“簇（cluster）”，聚類既能作為一個單獨過程，用於找尋數據內在的分佈結構，也可作為分類等其他學習任務的前去過程。——《Machine Learning》

聚類演算法也許是機器學習中“新演算法”出現最多、最快的領域，一個重要的原因是聚類不存在客觀標準，給定數據集總能從某個角度找到以往演算法未覆蓋的某種標準從而設計出新演算法。Kmeans演算法十分簡單易懂而且非常有效，但是合理的確定K值和K個初始類簇中心點對於聚類效果的好壞有很大的影響。眾多的論文基於此都提出了各自行之有效的解決方案，新的改進演算法仍然不斷被提出，此類文章大家可以在Web Of Science中搜索。

儘管Kmeans演算法在MATLAB、Python等語言的工具箱函數中都有自帶的函數可供調用，但作為機器學習的研究者新來說要設計出新的演算法，有時就得“定製”自己的Kmeans函數了。自己動手編寫無疑也更加能理解演算法的具體過程，接下來就讓我們進入正題吧

2. Kmeans演算法的原理與理解

Kmeans演算法是最常用的聚類演算法，主要思想是:在給定K值和K個初始類簇中心點的情況下，把每個點(亦即數據記錄)分到離其最近的類簇中心點所代表的類簇中，所有點分配完畢之後，根據一個類簇內的所有點重新計算該類簇的中心點(取平均值)，然後再迭代的進行分配點和更新類簇中心點的步驟，直至類簇中心點的變化很小，或者達到指定的迭代次數。

2.1 基本原理

假定給定數據樣本X，包含了n個對象\(X=\left \{ X_{1} ,X_{2},X_{3},...,X_{n}\right \}\),其中每個對象都具有m個維度的屬性。Kmeans演算法的目標是將n個對象依據對象間的相似性聚集到指定的k個類簇中，每個對象屬於且僅屬於一個其到類簇中心距離最小的類簇中。對於Kmeans，首先需要初始化k個聚類中心\(\left \{ C_{1} ,C_{2},C_{3},...,C_{k}\right \},1<k\leq n\),然後通過計算每一個對象到每一個聚類中心的歐式距離，如下式所示

上式中，\(X_{i}\)表示第i個對象\(1\leq i\leq n\),\(C_{j}\)表示第j個聚類中心的\(1\leq j\leq k\)，\(X_{it}\)表示第i個對象的第t個屬性，\(1\leq t\leq m\)，\(C_{jt}\)表示第j個聚類中心的第t個屬性。

依次比較每一個對象到每一個聚類中心的距離，將對象分配到距離最近的聚類中心的類簇中，得到k個類簇\(\left \{ S_{1},S_{2},S_{3},...,S_{k} \right \}\)

Kmeans演算法用中心定義了類簇的原型，類簇中心就是類簇內所有對象在各個維度的均值，其計算公式如下

式中，\(C_{l}\)表示第l個聚類的中心，\(1\leq l\leq k\)，\(\left | S_{l} \right |\)表示第l個類簇中對象的個數，\(X_{i}\)表示第l個類簇中第i個對象，\(1\leq i\leq\left | S_{l} \right |\)。

2.2 演算法流程

輸入：樣本集\(D=\left \{ x_{1},x_{2},x_{3},...,x_{m} \right \}\)；聚類簇數k.
過程：
1：從D中隨機選擇k個樣本作為初始均值向量\(\left \{ \mu _{1},\mu _{2},\mu _{3},...,\mu _{k} \right \}\)
2：repeat
3： 令\(C_{i}=\varnothing (1\leqslant i\leqslant k)\)
4： for j=1,2,...,m do
5： 計算樣本\(x_{j}\)與各均值向量\(\mu_{i}(1\leqslant i\leqslant k)\)的距離：\(d_{ji}=\left \| x_{j}-\mu_{i} \right \|_{2}\);
6： 根據距離最近的均值向量確定\(x_{j}\)的簇標記：\(\lambda _{j}=arg min_{i\in \left \{ 1,2,3,...,k \right \}}d_{ji}\)；
7： 將樣本\(x_{j}\)劃入相應的簇：\(C_{\lambda_{j}}=C_{\lambda_{j}}\cup \left \{ x_{j} \right \}；\)
8： end for
9： for i=1,2,...,k do
10: 計算新均值向量：\(\mu_{i}^{'}=\frac{1}{\left | C_{i} \right |}\sum _{x\in C_{i}}x\);
11： if \(\mu_{i}^{'}\neq \mu_{i}\) then
12： 將當前均值向量 \(\mu_{i}\)更新為\(\mu_{i}^{'}\)
13： else
14： 保持當前均值不變
15： end if
16： end for
17：until 當前均值向量均未更新
輸出：簇劃分\(C=\left \{ C_{1} ,C_{2},...,C_{k} \right \}\)

以上演算法流程引自周志華《機器學習》，從流程來看K-means演算法計算步驟基本上可以概括為兩個部分：（1）計算每一個對象到類簇中心的距離；（2）根據類簇內的對象計算新的簇類中心。

3. 編程實現

為了方便應用我們將其編寫為一個M函數KMeans()，首先需要確定函數的輸入輸出。這裡輸入參數為：data，K，iniCentriods，iterations（其中data為輸入的不帶標號的數據集數據矩陣，大小為numOfDatanumOfAttributes，K為數據分的類簇數目，iniCentriods為自行指定的初始聚類中心矩陣，大小為KnumOfAttributes，iterations為演算法迭代次數。）
輸出參數為：Idx，centroids，Distance（Idx為返回的分類標號， centroids為每一類的中心，Distance為類內總距離）

根據前面2.2節中的演算法流程編寫Kmeans演算法的MATLAB程式如下

%% Kmeans演算法
% 輸入：
% data 輸入的不帶分類標號的數據
% K 數據一共分多少類
% iniCentriods 自行指定初始聚類中心
% iterations 迭代次數

% 輸出：
% Idx 返回的分類標號
% centroids 每一類的中心
% Distance 類內總距離

 
function [Idx,centroids,Distance]=KMeans(data,K,iniCentriods,iterations)
[numOfData,numOfAttr]=size(data); % numOfData是數據個數，numOfAttr是數據維數
centroids=iniCentriods;
%% 迭代
for iter=1:iterations
    pre_centroids=centroids;% 上一次求得的中心位置
    
    tags=zeros(numOfData,K);
    %% 尋找最近中心，更新中心
    for i=1:numOfData
        D=zeros(1,K);% 每個數據點與每個聚類中心的標準差
        Dist=D;
        
        % 計算每個點到每個中心點的標準差
        for j=1:K
            Dist(j)=norm(data(i,:)-centroids(j,:),2);
        end
        
        [minDistance,index]=min(Dist);% 尋找距離最小的類別索引
        tags(i,index)=1;% 標記最小距離所處的位置（類別）
    end
    
    
    %% 取均值更新聚類中心點
    for i=1:K
        if sum(tags(:,i))~=0
            % 未出現空類，計算均值作為下一聚類中心
            for j=1:numOfAttr
                centroids(i,j)=sum(tags(:,i).*data(:,j))/sum(tags(:,i));
            end
        else % 如果出現空類，從數據集中隨機選中一個點作為中心
            randidx = randperm(size(data, 1));
            centroids(i,:) = data(randidx(1),:);
            tags(randidx,:)=0;
            tags(randidx,i)=1;
        end
    end
    
   
    if sum(norm(pre_centroids-centroids,2))<0.001  % 不斷迭代直到位置不再變化
        break;
    end
    
    
end

%% 計算輸出結果
Distance=zeros(numOfData,1);
Idx=zeros(numOfData,1);
for i=1:numOfData
    D=zeros(1,K);% 每個數據點與每個聚類中心的標準差
    Dist=D;
    % 計算每個點到每個中心點的標準差
    for j=1:K
        Dist(j)=norm(data(i,:)-centroids(j,:),2);
    end
    
    [distance,idx]=min(Dist);% 尋找距離最小的類別索引
    distance=Dist(idx);
    
    Distance(i)=distance;
    Idx(i)=idx;
end
Distance=sum(Distance,1);% 計算類內總距離
end

在以上代碼中其最主要部分在於第18至58行，進行尋找最近中心和求取均值更新聚類中心點。值得註意的是，在聚類過程中可能會出現空類即代碼第44行那樣，為保證演算法的繼續運行，從數據集中隨機選取一個點作為中心。

4. 聚類結果評價

為了驗證編寫的Kmeans函數的性能，這裡對想用的UCI數據集Iris數據集進行聚類並計算聚類的準確率，Iris數據集可以在http://archive.ics.uci.edu/ml/index.php上下載得到。首先讀取Iris數據集，自行指定初始聚類中心調用前面編寫的KMeans函數進行聚類，然後計算聚類的準確率，其代碼如下

clear 
data=load('Iris.txt');
data=data(:,2:end);

matrix=[5.9016,2.7484,4.3935,1.4339;6.8500,3.0737,5.7421,2.0711;5.0060,3.4280,1.4620,0.2460];
[Idx,C,distance]=KMeans(data,3,matrix,500);
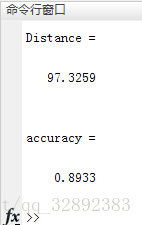
Distance=sum(distance)

c1=Idx(1:50,1);c2=Idx(51:100,1);c3=Idx(101:150,1);
accuracy=(sum(c1==mode(Idx(1:50,1)))+sum(c2==mode(Idx(51:100,1)))+sum(c3==mode(Idx(101:150,1))))/150

為方便使用Iris數據集經過了一些整理，這裡將最後一列的帶字元串的標簽Iris-setosa，Iris-versicolor，Iris-virginica分別用數字1,2,3代替並移到了第一列，所以第三行選取的是從第二列至最後一列的數據。第5行中的matrix是查閱論文得到的一個初始聚類中心，正好用來比對聚類結果。第6行則調用KMeans()函數進行聚類，得到聚類標號和類內距離。對每類的類內距離求和即得到總的距離Distance，如第7行。準確率的計算有點麻煩，因為不能直接用KMeans計算後得到的標號跟原數據集中的標號對比計算準確率，KMeans只需要也只能將那些“相似”的數據點聚集到一類中，而給這一類數據的標號卻是可能跟原數據集不同的。

這裡採用一個簡單的方法，從原數據集的標簽可以看出第1-50個數據點為一類（Iris-setosa），第51-100為一類（Iris-versicolor），第101-150為一類（Iris-virginica），因此只需確定每50個數據點中的聚類標號是不是一致。取它們之中數目最多的標號作為正確的個數，最終比上數據集的總數即為準確率。以上代碼運行結果如下所示。

5. 類簇中心點的選取

KMeans演算法本身思想比較簡單，但是合理的確定K值和K個初始類簇中心點對於聚類效果的好壞有很大的影響。最簡單的確定初始類簇中心點的方法是隨機產生數據大小範圍內的K個點作為初始的簇類中心點。隨機產生初始點併進行測試的程式代碼如下

clear
data=load('Iris.txt');
data=data(:,2:end);
K=3;


%% 產生隨機初始點
[numOfData,numOfAttr]=size(data);   % numOfData是數據個數，numOfAttr是數據維數

centroids=zeros(K,numOfAttr);       % 隨機初始化，最終迭代到每一類的中心位置
maxAttr=zeros(numOfAttr);        % 每一維最大的數
minAttr=zeros(numOfAttr);        % 每一維最小的數
for i=1:numOfAttr
    maxAttr(i)=max(data(:,i));    % 每一維最大的數
    minAttr(i)=min(data(:,i));    % 每一維最小的數
    for j=1:K
        centroids(j,i)=maxAttr(i)+(minAttr(i)-maxAttr(i))*rand();  % 隨機初始化，選取每一維[min max]中初始化
    end
end

[Idx,C,distance]=KMeans(data,K,centroids,500);% 調用KMeans
Distance=sum(distance)% 計算類內距離之和

%% 計算準確率
c1=Idx(1:50,1);c2=Idx(51:100,1);c3=Idx(101:150,1);
Accuracy=(sum(c1==mode(Idx(1:50,1)))+sum(c2==mode(Idx(51:100,1)))+sum(c3==mode(Idx(101:150,1))))/numOfData

可以多運行幾次以上代碼，可以看出由於初始點事隨機選取的每次運行得到的結果有所差異。這也是基本Kmeans演算法的一個缺點，隨著眾多改進演算法的提出Kmeans演算法的這一問題也得到改善，深入瞭解的朋友可以查閱相關論文。

6. 結束語

本博文的完整MATLAB程式文件與整理好的數據集文件已經上傳，下載即可運行。下載地址如下

點擊下載：本文Kmeans演算法M函數及測試完整文件

【公眾號獲取】
    本人微信公眾號已創建，掃描以下二維碼並關註公眾號“AI技術研究與分享”，後臺回覆“KM20180516”即可獲取全部資源文件信息。

由於編者能力有限，代碼即使經過了多次校對，也難免會有疏漏之處。希望您能熱心指出其中的錯誤，以便下次修改時能以一個更完美更嚴謹的樣子，呈現在大家面前。同時如果有更好的實現方法也請您不吝賜教。