前端程式員學好演算法系列（七）二叉樹和遞歸

144. 二叉樹的前序遍歷
給定一個二叉樹，返回它的 前序 遍歷。

示例:

輸入: [1,null,2,3] 
1
\
2
/
3

輸出: [1,2,3]

有兩種通用的遍歷樹的策略：

深度優先搜索（DFS）

在這個策略中，我們採用深度作為優先順序，以便從跟開始一直到達某個確定的葉子，然後再返回根到達另一個分支。

深度優先搜索策略又可以根據根節點、左孩子和右孩子的相對順序被細分為前序遍歷，中序遍歷和後序遍歷。

寬度優先搜索（BFS）

我們按照高度順序一層一層的訪問整棵樹，高層次的節點將會比低層次的節點先被訪問到。

下圖中的頂點按照訪問的順序編號，按照 1-2-3-4-5 的順序來比較不同的策略。

解題：
1. 前序遍歷口訣，遞歸終止條件 if(root==null) return
2. 前序遍歷先列印root的值，遞歸遍歷root的左子樹， 遞歸調用root的又子樹

3. 中序遍歷 先遞歸遍歷root的左子樹，列印root的值， 遞歸調用root的又子樹

4. 後序遍歷 先遞歸遍歷root的左子樹， 在遞歸調用root的又子樹， 列印root的值

5.前中後序遍歷的不同之處在於列印root.val的時機，掌握一種，其他也很好掌握

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var preorderTraversal = function(root) {
     let res = []
     function pre(root){
         if(root==null){
             return
         }
         res.push(root.val)
         if(root.left){
              pre(root.left)
         }
         if(root.right){
              pre(root.right)
         }
     }
     pre(root)
     return res
};

104. 二叉樹的最大深度
給定一個二叉樹，找出其最大深度。

二叉樹的深度為根節點到最遠葉子節點的最長路徑上的節點數。

說明: 葉子節點是指沒有子節點的節點。

示例：

給定二叉樹 [3,9,20,null,null,15,7]，

3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。

解題：

我們知道，二叉樹每個節點的深度與它左右子樹的深度有關，且等於其左右子樹最大深度值加上 1 。即：maxDepth(root) = max(maxDepth(root.left),maxDepth(root.right)) + 1

以 [3,4,20,null,null,15,7] 為例：

<1>我們要對根節點的最大深度求解，就要對其左右子樹的深度進行求解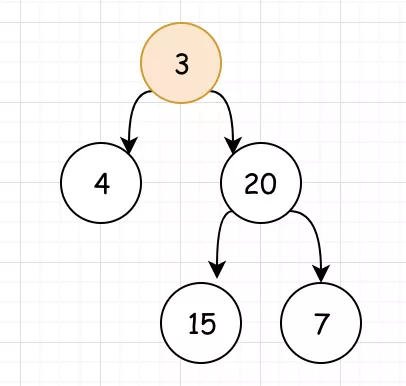

<2>我們看出。以4為根節點的子樹沒有左右節點，其深度為 1 。而以 20 為根節點的子樹的深度，同樣取決於它的左右子樹深度。

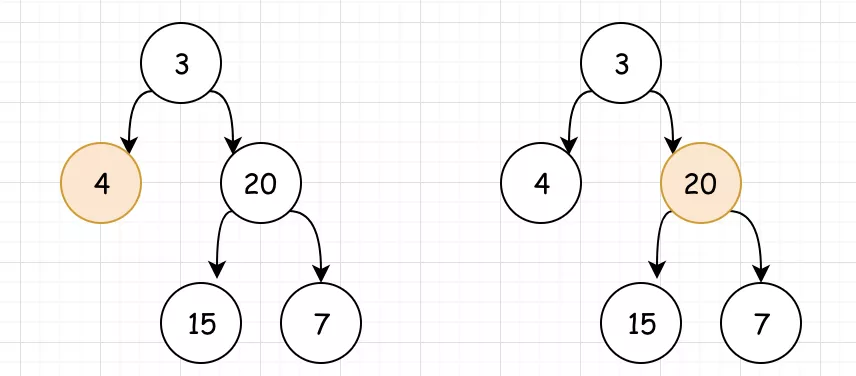
<3>對於15和7的子樹，我們可以看出其深度為 2

/**
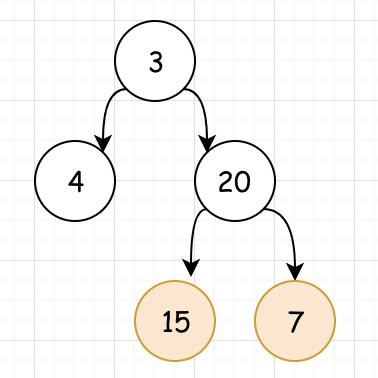
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    if(root==null){
        return 0
    }
    return Math.max(maxDepth(root.left),maxDepth(root.right))+1
};

226. 翻轉二叉樹
翻轉一棵二叉樹。

示例：

輸入：

4
/ \
2 7
/ \ / \
1 3 6 9
輸出：

4
/ \
7 2
/ \ / \
9 6 3 1

解題：

1.js交換兩個值A,B的重要事項 先緩存A  let tmp = A  ； 把A賦值B A = B； 把B賦值為緩存的tmp

2.我們這裡也一樣 遞歸終止條件 if(!root) return null

3.root存在時交換左右節點，在遞歸調用

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function(root) {
    if(!root) return null
    if(root) {
        var left = root.left
        root.left = root.right
        root.right = left
    }
    invertTree(root.left)
    invertTree(root.right)
    return root
};

112. 路徑總和
給定一個二叉樹和一個目標和，判斷該樹中是否存在根節點到葉子節點的路徑，這條路徑上所有節點值相加等於目標和。

說明: 葉子節點是指沒有子節點的節點。

示例: 

給定如下二叉樹，以及目標和 sum = 22，

5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1

返回 true, 因為存在目標和為 22 的根節點到葉子節點的路徑 5->4->11->2。

解題：

1.求解從 root 到葉子節點是否存在路徑和為 sum 的路徑 hasPathSum(root, sum)，可以轉換成求解從 root.left 或者 root.right 到葉子節點是否存在路徑和為 sum - root.val 的路徑，即 hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val) 。

2.本題要求必須有葉子節點所有 當root只有一個元素且root.val ==sum時不是一個正確的解。
3.我們用 root.left==null && root.right==null 時判斷最正確的解。

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} sum
 * @return {boolean}
 */
var hasPathSum = function(root, sum) {
      if(root==null){
          return false
      }
      if(root.left==null && root.right==null){
          return sum == root.val
      }
      if(hasPathSum(root.left,sum-Number(root.val))){
          return true
      }
      if(hasPathSum(root.right,sum-Number(root.val))){
          return true
      }
      return false
};