前端程式員學好演算法系列（九）遞歸回溯演算法

回溯演算法主要應用於樹形問題，我們先從一個簡單的演算法入手

17. 電話號碼的字母組合
給定一個僅包含數字 2-9 的字元串，返回所有它能表示的字母組合。

給出數字到字母的映射如下（與電話按鍵相同）。註意 1 不對應任何字母。

示例:

輸入："23"
輸出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

解題：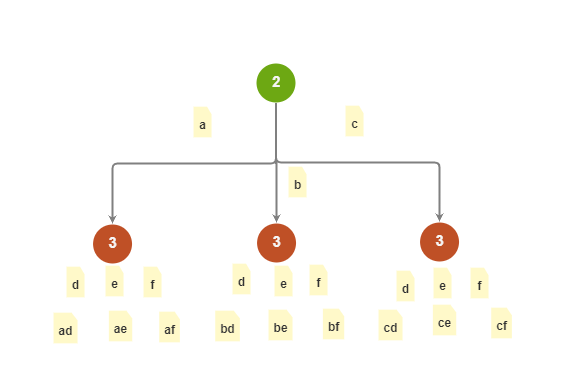

digits是數字字元串
s(digits) 是digits所能代表的字元串
s(digits[0..n-1])
  = letter(digits[0]) +s(digits[1...n-1])
  =letter(digits[0]) + letter(digits[1])  +s(digits[2...n-1])

1.我們建立一個map的數據結構，把鍵盤數字代表的字母一一傳入map中； map.get(digits[i])為當前傳入的第i個字元代表的字母集合

2. _generate() 我們傳入兩個變數 i 當前選擇的第幾個字母，str 預設傳入''
3. 當i的值等於digits.length是我們獲得了一個結果push到result中
4.迴圈當前的數字代表的字母 ，一一傳入_generate(i+1,str+tmp[r]);  遍歷其他結果

/**
 * @param {string} digits
 * @return {string[]}
 */
var letterCombinations = function(digits) {
     if(!digits){
        return [];
    }
    var len = digits.length;
    var map = new Map();
    map.set('1','');
    map.set('2','abc');
    map.set('3','def');
    map.set('4','ghi');
    map.set('5','jkl');
    map.set('6','mno');
    map.set('7','pqrs');
    map.set('8','tuv');
    map.set('9','wxyz');
    var result = [];
    function _generate(i,str){
        
        if(i == len){
            result.push(str);
            return;
        }
        var tmp = map.get(digits[i]);
        for(var r = 0;r<tmp.length;r++){
            _generate(i+1,str+tmp[r]);
        }
    }
    _generate(0,'');
    return result;
};

46. 全排列
給定一個 沒有重覆 數字的序列，返回其所有可能的全排列。

示例:

輸入: [1,2,3]
輸出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

 解題：
1.回溯標準解題模板res 存放結果的數組，tmpPath為傳入的數組，當 tmpPath.length == n是我們得到一個滿足條件的解，
2. !tmpPath.includes(nums[i]) 來過濾防止數組tmpPath存在重覆的值
3. tmpPath.push(nums[i]); 數組中加入值後，遞歸完成後，相應的值需要從數組中減去，tmpPath.pop()
4.數組為引用類型，防止取值錯誤我們取 tmpPath.slice()繼續遍歷
5.每次遍歷index+1 進行下次遍歷

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function(nums) {
    let n = nums.length;
    let res = [];
    let tmpPath = [];
    let backtrack = (index,tmpPath) => {
        if(tmpPath.length == n){
            res.push(tmpPath);
            return;
        }
        for(let i = 0;i < n;i++){
            if(!tmpPath.includes(nums[i])){
                tmpPath.push(nums[i]);
                backtrack(index+1,tmpPath.slice());
                tmpPath.pop();
            }
        }
    }
    backtrack(0,tmpPath);
    return res;
  
}

77. 組合
給定兩個整數 n 和 k，返回 1 ... n 中所有可能的 k 個數的組合。

示例:

輸入: n = 4, k = 2
輸出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

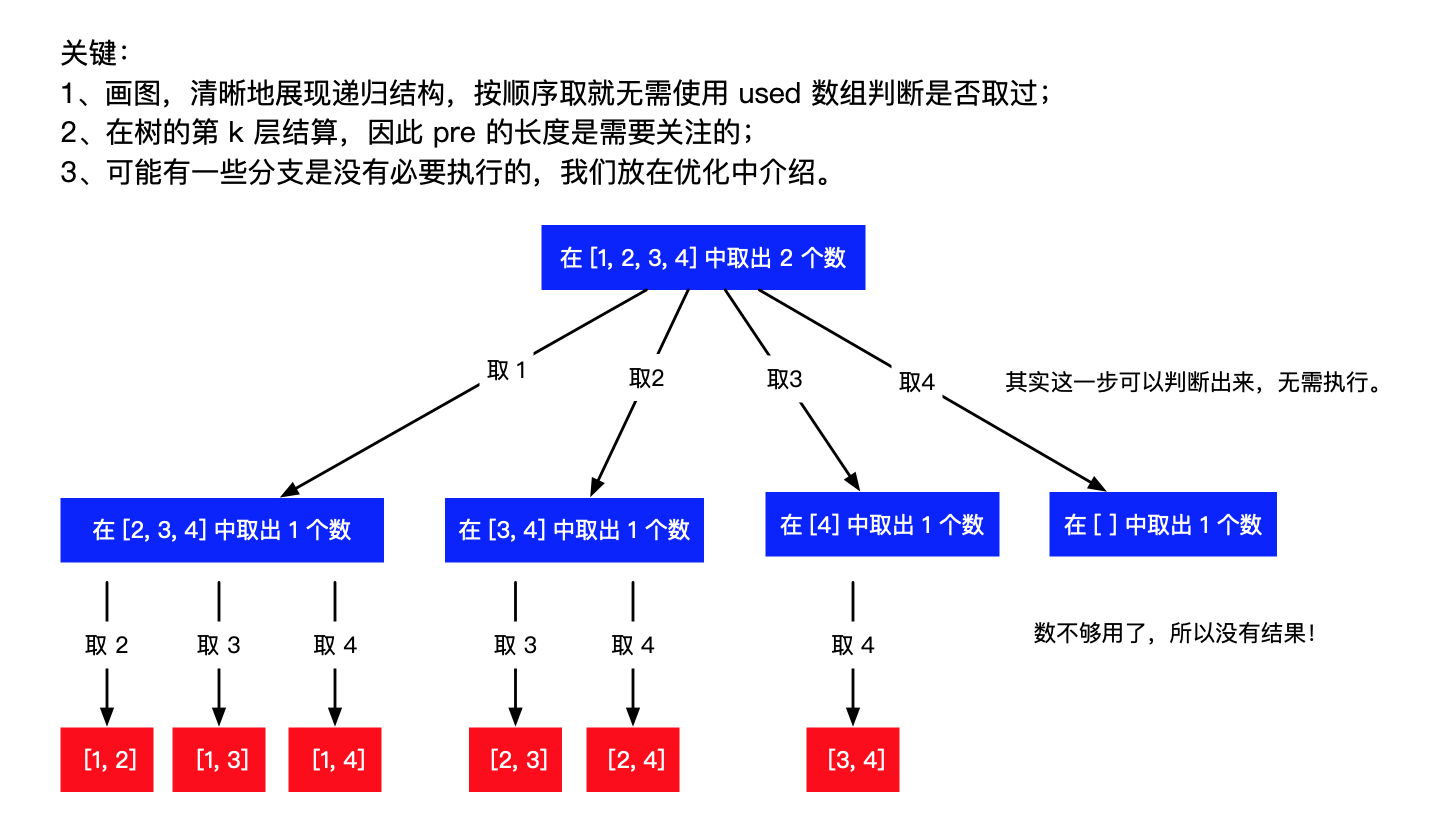
1.求解n,k,當前已經找到的組合儲存在res中，需要從start位置處開始搜索

2.could.length == k我們獲得了一個滿足條件的解

3. could.push(i)  could.pop() 每次我們加入的數據在遞歸結果前需要刪除掉
4.每次遞歸迴圈時從i的下一位開始找

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function(n, k) {
   
    var res = [];
    var could = [];
    if(k==0){
        return [[]]
    }
    function dfs(start,n,res,could){
        if(could.length == k){
            res.push(could.slice(0));
            return;
        }
        for(var i = start ; i<n+1;i++){
            could.push(i);
            dfs(i+1,n,res,could);
            could.pop()
        }
        return res;
    }
    return dfs(1,n,res,could)

};