仿射期限結構模型:理論與實現——實現部分 [toc] 本文介紹如何以面向對象的方式實現 " Affine Term Structure Models: Theory and Implementation " 中的演算法,並適當的使用設計模式使代碼儘可能的優雅。 引言 金融工程領域的模型和方法之間既有強 ...
仿射期限結構模型:理論與實現——實現部分
目錄
本文介紹如何以面向對象的方式實現 Affine Term-Structure Models: Theory and Implementation 中的演算法,並適當的使用設計模式使代碼儘可能的優雅。
引言
金融工程領域的模型和方法之間既有強烈的共性,又有鮮明的個性,這使得“設計模式”的應用順理成章。
金融計算程式中常見的幾個設計模式有:
- 模板方法模式
- 策略模式
- 包裝器模式

AffineModel 類與模板方法模式
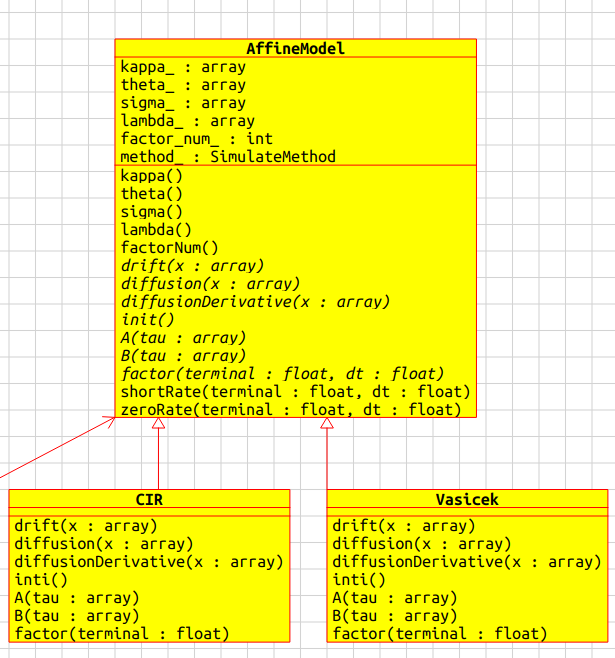
首先要實現的是 AffineModel 類,它主要負責模擬因數、短期利率和零息利率的路徑。
對於仿射模型來說,由因數計算短期利率和零息利率的過程是一致的,這部分代碼放到基類中,具體的派生類(Vasicek 和 CIR)只要專註實現模擬因數路徑的計算就可以了。
基類規劃整體計算流程,派生類分別實現整體流程中的細節,這便是“模板方法模式”典型的應用場景。
SimulateMethod 類與策略模式
在當前案例中,因數路徑的模擬可以使用 Euler 和 MIlstein 這類通用的離散方法,也可以使用卡爾曼濾波框架下的轉移矩陣法。
上述方法僅需要知道模型非常基本的信息(例如漂移項、擴散項和參數)便可以工作,因此可以獨立於 AffineModel 類存在,而又被 AffineModel 對象使用。
將方法抽象成類,再提供給其他類使用,這便是“策略模式”典型的應用場景。

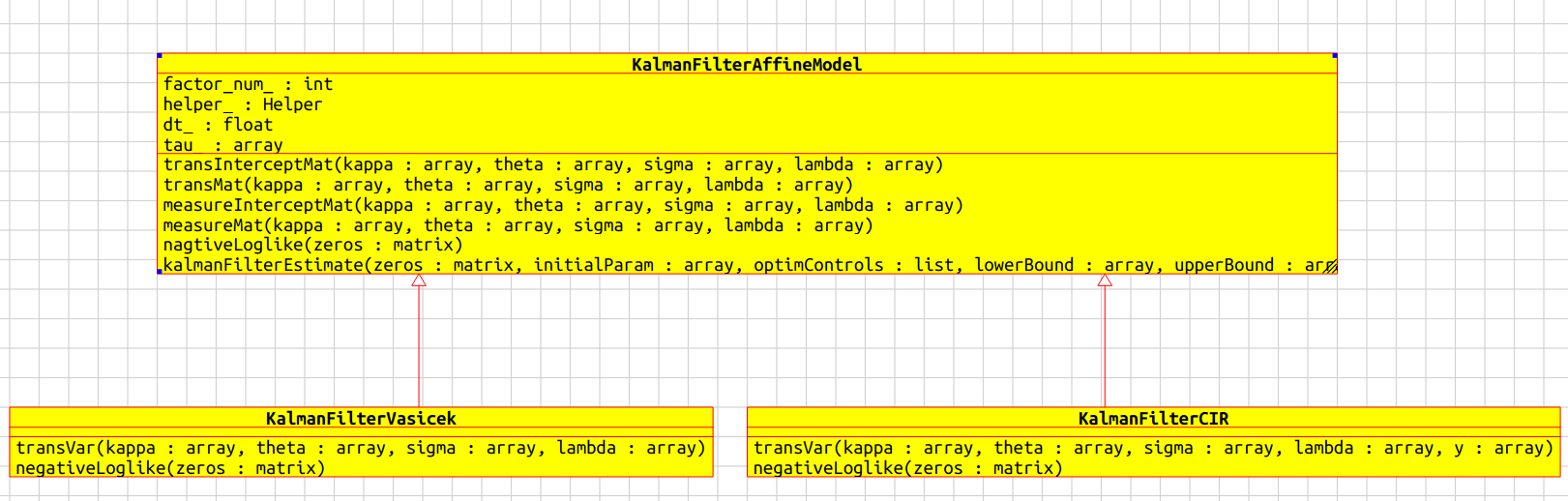
KalmanFilterAffineModel 類
KalmanFilterAffineModel 類負責根據零息利率的歷史數據估計出模型參數,整個計算過程圍繞觀測系統和轉移系統中出現的五個關鍵矩陣展開:
- 觀測矩陣
- 觀測截矩矩陣
- 轉移矩陣
- 轉移截矩矩陣
- 轉移協方差矩陣
模型參數蘊涵在這五個矩陣中,藉由矩陣和利率數據,通過卡爾曼濾波演算法可以算出特定模型參數對應的似然函數值,通過最大化似然函數值就可以估計利率數據對應的模型參數。
在當前案例中,五個矩陣中的前四個僅和模型參數有關,且演算法一致,可以放到基類中,最後一個由各個派生類自己實現。
似然函數的計算也由各個派生類自己實現,而最優化部分的代碼放在基類中。KalmanFilterAffineModel 類展示了一個中規中矩的面向對象設計案例,稍稍用到了“模板方法模式”。
KalmanFilterVasicek在似然函數的計算部分藉助快速卡爾曼濾波(FKF)。
Helper 類與包裝器模式
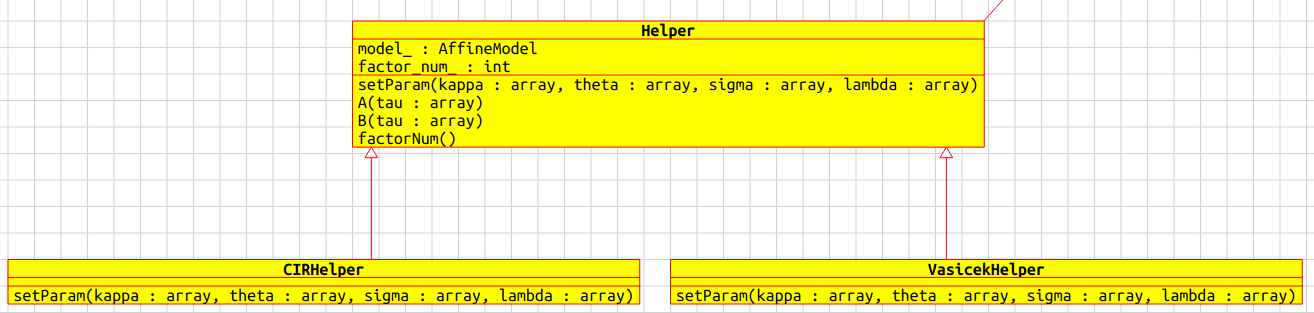
KalmanFilterAffineModel 類中計算關鍵矩陣的時候涉及到仿射模型中 \(A(\tau)\) 和 \(B(\tau)\) 的計算,而這部分代碼已經出現在 AffineModel 類中。
為了僅復用這部分代碼,而不是其他,需要在 AffineModel 類的外側套一層“殼”,屏蔽一些介面。Helper 類充當了這個角色,有選擇的暴露出介面 A(tau) 和 B(tau) 為 KalmanFilterAffineModel 類使用。
復用某些類已有的代碼,而以不同的介面形式呈現,併為其他類所用,這便是“包裝器模式”典型的應用場景。
KalmanFilterAffineModel類和Helper類之間是策略模式的關係。
源代碼
Affine Term-Structure Models: Theory and Implementation
註意:CIR 的部分運行速度很慢,未被充分測試。



