漢諾塔簡介 最近在看數據結構和演算法,遇到了一個非常有意思的問題——漢諾塔問題。 先看下百度百科是怎麼定義漢諾塔的規則的: 漢諾塔(又稱河內塔)問題是源於印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子,在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下麵 ...
漢諾塔簡介
最近在看數據結構和演算法,遇到了一個非常有意思的問題——漢諾塔問題。
先看下百度百科是怎麼定義漢諾塔的規則的:
漢諾塔(又稱河內塔)問題是源於印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子,在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下麵開始按大小順序重新擺放在另一根柱子上。並且規定,在小圓盤上不能放大圓盤,在三根柱子之間一次只能移動一個圓盤。
額,好吧,好像有點啰里啰嗦的。其實一句話就是,在三個柱子之間移動盤子,一次只能移動一個,並且要保證每一步上邊的盤子都要比下邊的盤子小,最終實現把所有的盤子都從最左邊柱子移動到最右邊的柱子上。
我找了一個小游戲,可以玩一下,體驗一下這個過程。相信我,你玩不過第五關的!嘿嘿,玩不過再過來看一下,我是怎麼給你做游戲攻略(作弊)的。
地址:http://www.4399.com/flash/109504_1.htm

我相信,有很多童鞋在學遞歸的時候,都會受到這個問題的困擾。彆著急,你不是一個人,我第一次看到這個也是一臉懵逼,這什麼鬼啊,這麼複雜。下麵我通過圖解的方式,演示整個移動過程,幫助你理解用遞歸解決這個問題的思想。
漢諾塔圖解
我們一步一步從簡單到複雜。為了方便,我把三個柱子從左到右分別叫 A,B,C。盤子的數字從上到下依次增大。
一個盤子
只有一個盤子的時候,就比較簡單了。如圖,只需要一步,直接把 第 1 個盤子從 A移動到 C就完成了。
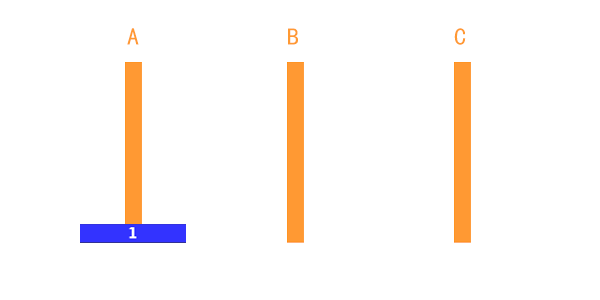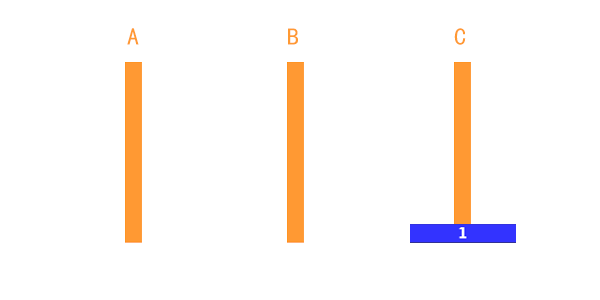
兩個盤子
兩個盤子的時候,也比較簡單,如下圖,只需要藉助一下 B 柱子即可完成。
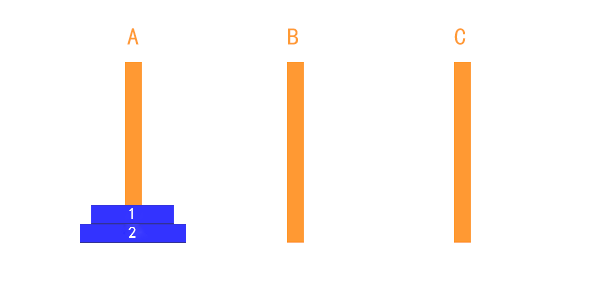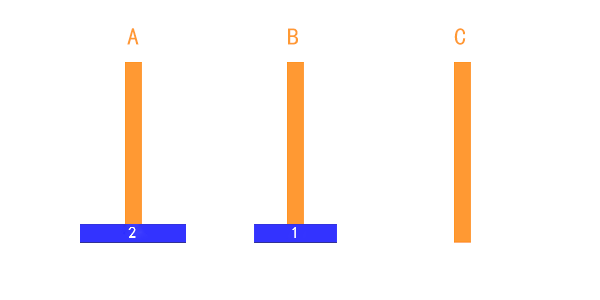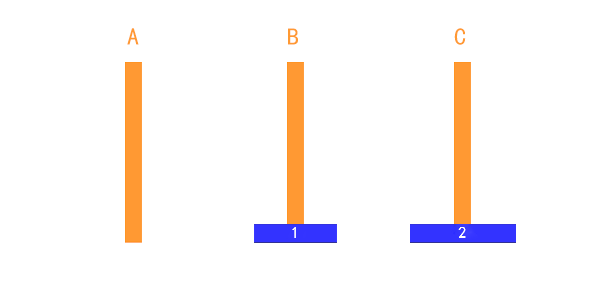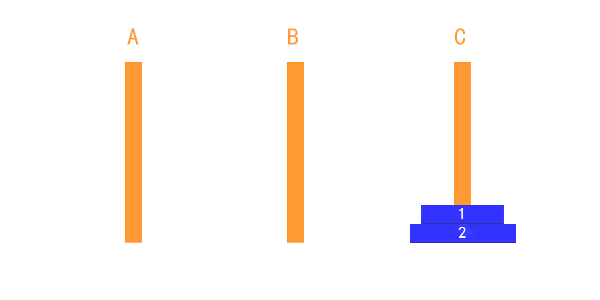
這個過程可以表述為:
把第1個盤子從A移到B
把第2個盤子從A移到C
把第1個盤子從B移到C
三個盤子
三個盤子的時候,稍微複雜一些,但是我們一般也是可以通過心算,把過程推演出來的。
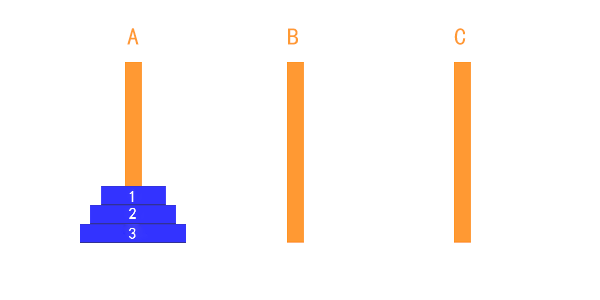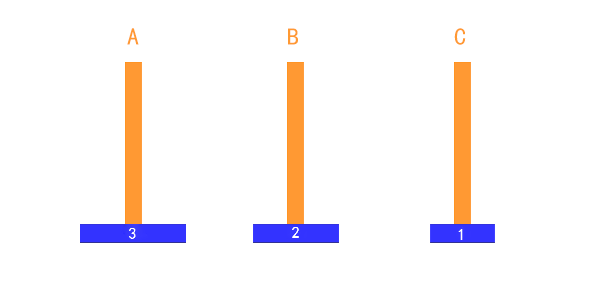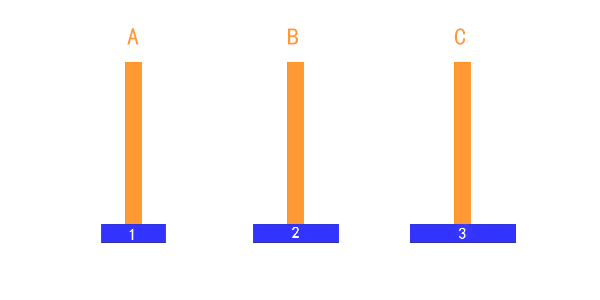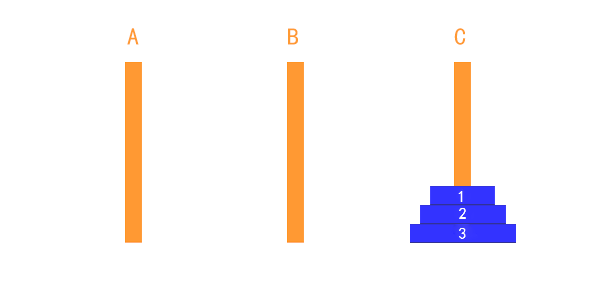
把第1個盤子從A移到C
把第2個盤子從A移到B
把第1個盤子從C移到B
把第3個盤子從A移到C
把第1個盤子從B移到A
把第2個盤子從B移到C
把第1個盤子從A移到C
n 個盤子
鐺鐺鐺,現在到了第四關了,我相信已經有部分小伙伴感覺開始吃力了,通過演算就不好搞了。如果你搞不出來,我們就藉助電腦來幫我們推算出來這個過程(哈哈,我是不是很機智)。
其實,通過前面的三個例子,我們可以發現,盤子的移動是有規律可循的。
細心的你有沒有發現,在每一步盤子移動的過程中,總會有一步,是下邊最大的盤子,從 A 移到 C 的。如,兩個盤子,就是第 2 個盤子從 A移到 C,三個盤子,就是第 3 個盤子從 A 移到 C。
仔細觀察,以三個盤子為例,把第 3 個盤子從 A 移動到 C 這一步,其實,第 1 個和第 2 個盤子是已經按順序擺放好了的,即一起放在中間的 B 柱子。
因此,我們可以把這個動作抽象出來,把除了最下邊的盤子之外的其他盤子看成一個整體。這樣的話,整個流程,就和兩個盤子的移動過程沒什麼兩樣了。總共就三步,我以四個盤子為例。看以下動畫,
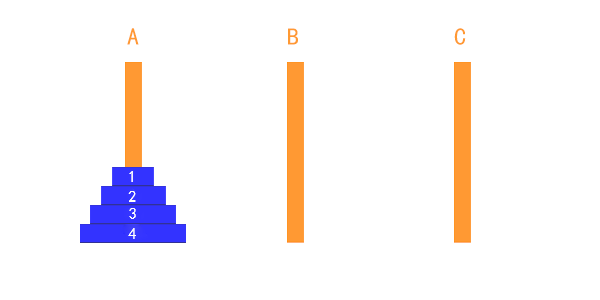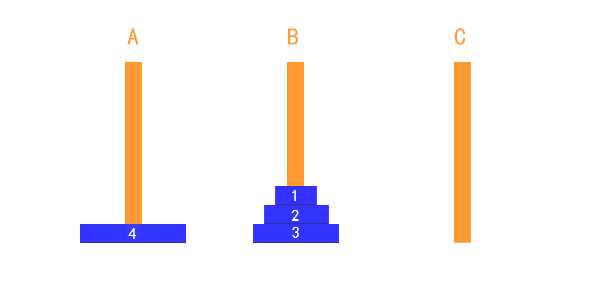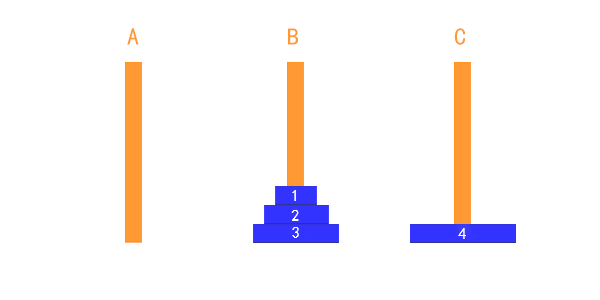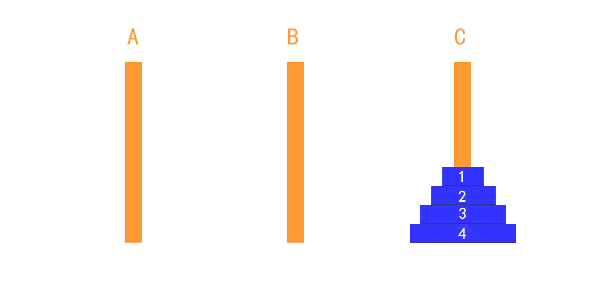
整個過程可以表述為:
把1,2,3盤子整體從 A 移到 B (可以認為是藉助 C 柱子移動的),
把第 4 個盤子從 A 移到 C(不需要藉助額外的柱子),
把1,2,3盤子整體從 B 移到 C(藉助 A 柱子)
但是,這隻是我們把它抽象出來的過程,游戲中不允許我們整體移動,怎麼辦呢。
好說,我把 1,2,3 這個整體再拆分,不就是三個盤子的移動過程嘛。完全可以把 1,2看成一個整體一起移動,3 單個移動,也是三步完成。然後再拆分,直到只有最後一個盤子的時候,就完成了整個過程。
所以,可以看到,這個拆分的過程,就是不斷遞歸的過程。而每次遞歸時,都可以把第 1 個盤子到 第 n-1 個盤子看成一個整體。每一次遞歸都是一個三步曲,藉助另外一個柱子,從當前柱子移動到目標柱子。看代碼,
public class HanioTest {
public static void main(String[] args) {
int n = 4;
char a = 'A',b = 'B',c = 'C';
hanio(n,a,b,c);
}
/**
*
* @param n 一共需要移動的盤子
* @param a 盤子移動的起始柱子
* @param b 藉助的柱子
* @param c 盤子需要移動到的目標柱子
*/
public static void hanio(int n,char a, char b, char c){
//只有一個盤子的時候,就直接從A移到C
if(n == 1){
move(n,a,c);
}else{
//三步曲,註意觀察,a,b,c三個的位置變化
//1.把 n-1 個盤子看成一個整體,藉助 C 從 A 移動到 B
hanio(n-1,a,c,b);
//2.把第 n 個盤子從 A 移動到 C
move(n,a,c);
//3.再把 n-1 盤子整體,藉助 A 從 B 移動到 C
hanio(n-1,b,a,c);
}
}
public static void move(int n , char a, char b){
System.out.println("把第"+ n +"個盤子從"+ a +"移到"+ b);
}
}
聰明的你,如果游戲第四關通關了,可以用來檢查一下這個代碼執行過程是否和你的移動過程一致。
第五關,如果你不藉助程式,能心算出來,我只能說你太厲害了,I 服了 YOU,佩服佩服。
那麼第六關,第七關呢。
結語
回到最開始,百度百科說要移動 64 片黃金圓盤,OMG 的,如果誰能手動計算出來,那才是真的大神(不過,話說,誰會這麼無聊呢,哈哈)。
感興趣的你也可以嘗試用程式跑一遍 64 片是什麼結果,我估計就算你機器性能很好,也得跑好長時間。。。
溫馨提示:機器炸了不怪我哦 ~
如果本文對你有用,歡迎點贊,評論,轉發。
學習是枯燥的,也是有趣的。我是「煙雨星空」,歡迎關註,可第一時間接收文章推送。



