章節簡介 前5篇博客寫的都是線性結構,對於有層級結構的數據需要用樹形結構來描述 本章的重要知識點 1. 理解有關樹的基本概念和二叉樹的基本概念 2. 掌握二叉樹的存儲結構以及遍歷方法 3. 掌握樹的存儲結構以及樹、森林、二叉樹的相互轉換方法 4. 梳理掌握哈夫曼樹構造方法和哈夫曼編碼的設計方法 樹的 ...
章節簡介
前5篇博客寫的都是線性結構,對於有層級結構的數據需要用樹形結構來描述
本章的重要知識點
- 理解有關樹的基本概念和二叉樹的基本概念
- 掌握二叉樹的存儲結構以及遍歷方法
- 掌握樹的存儲結構以及樹、森林、二叉樹的相互轉換方法
- 梳理掌握哈夫曼樹構造方法和哈夫曼編碼的設計方法
樹的基本概念
核心一句話
線性結構中一個結點至多只有一個直接後繼,樹形結構一個結點可以有一個或多個直接後繼
認識樹
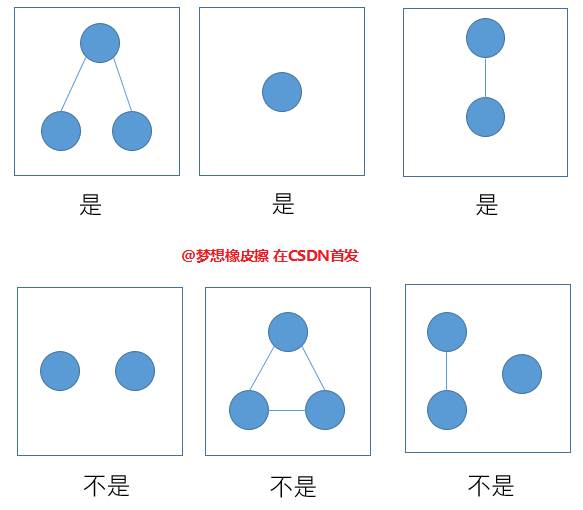
看圖即可,你要能區分出來哪些是樹,哪些不是樹
樹的相關術語
結點的度:樹上任意結點所擁有的子樹的數目稱為該結點的度
葉子:度為0的結點稱為葉子或者終端結點
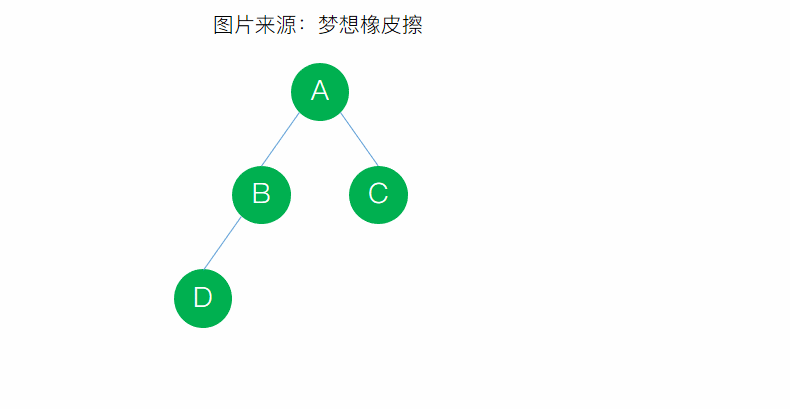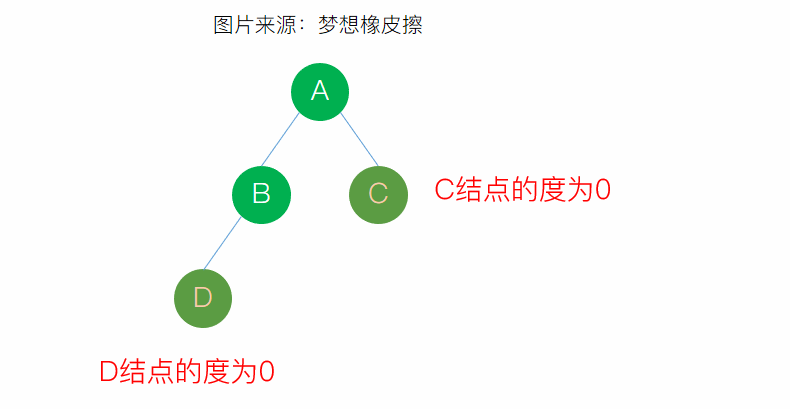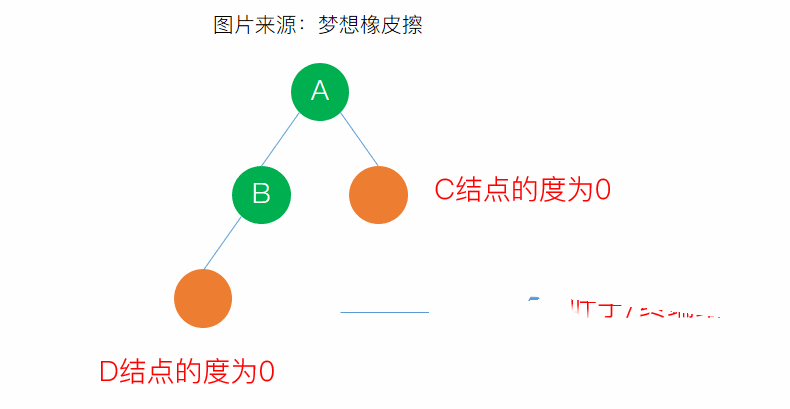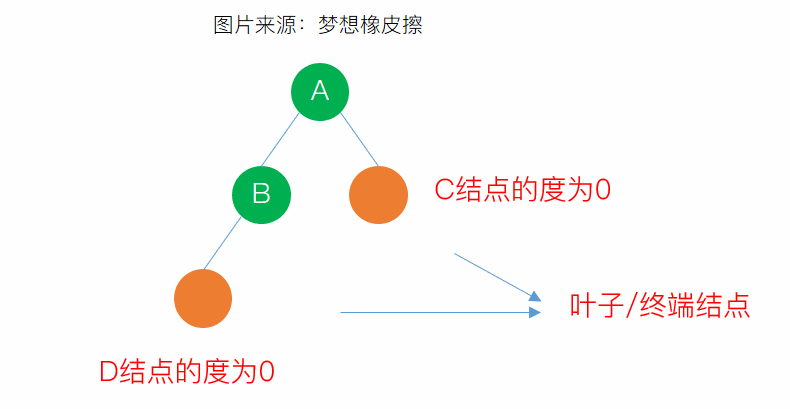
- 樹的度:一棵樹中所有結點的度的最大值稱為該樹的度,就是把所有結點的度求和
結點的層次:從根算起,根的層次為1,其餘結點的層次為其雙親的層次加1
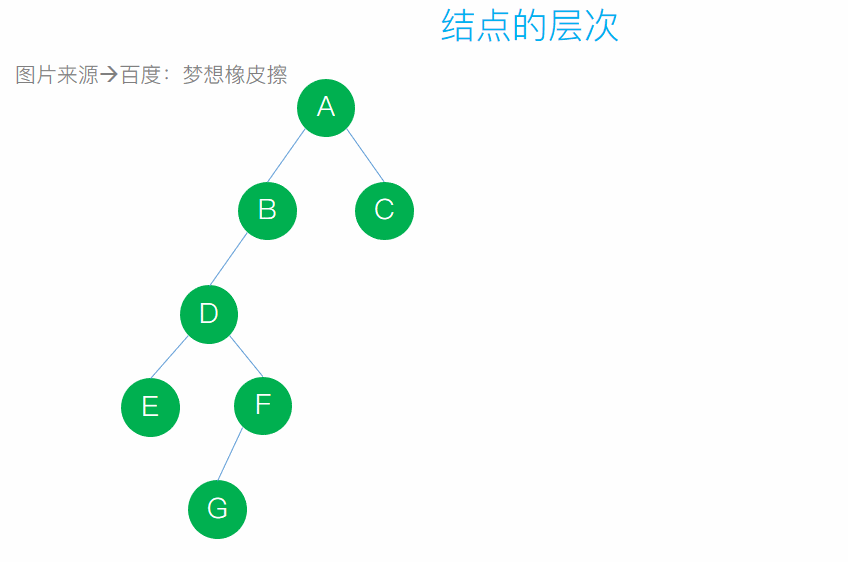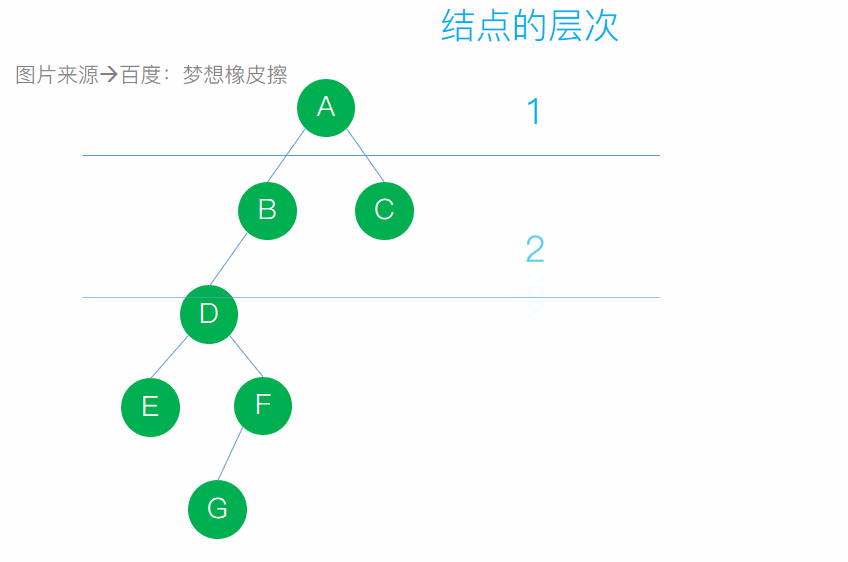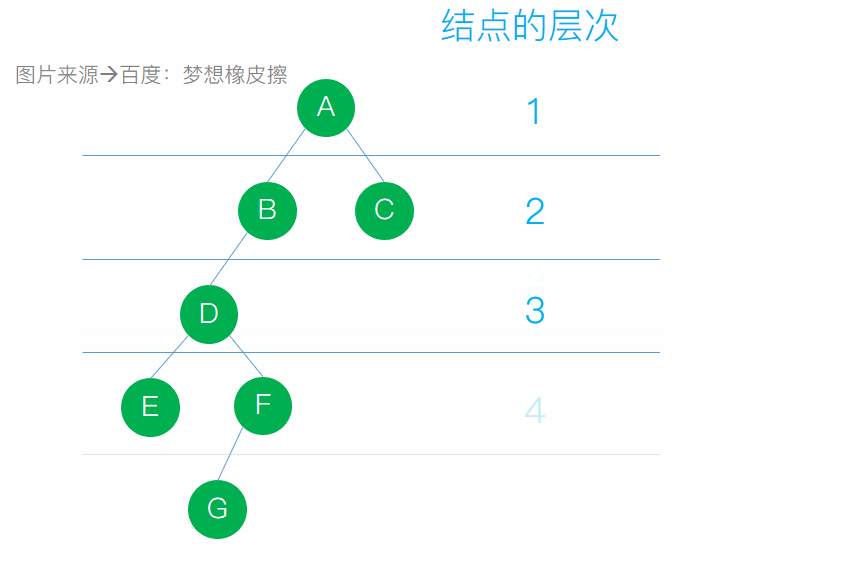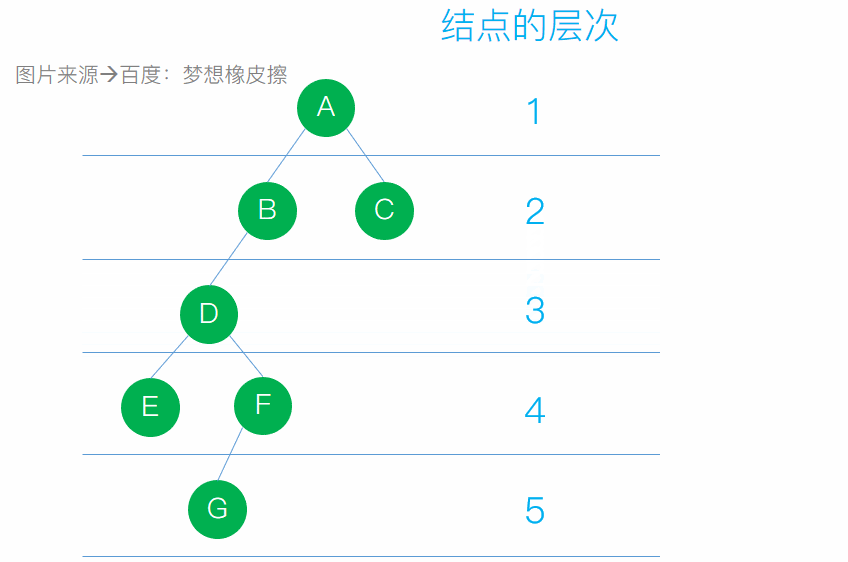
- 樹的高度:一棵樹中所有結點層次數的最大值稱為該樹的高度或
深度 還有一些小概念:有序樹、無序樹
樹的相關術語,一定要一開始就明確清晰,後面才好學習
二叉樹
官方概念:二叉樹是n(n≥0)個元素的有限集合,該集合或者為空,或者由一個根及兩棵互不相交的左子樹和右子樹組成,其中左子樹和右子樹也均為二叉樹。二叉樹的任一結點都有兩棵子樹(它們中的任何一個都可以是空子樹),並且這兩棵子樹之間有次序關係,交換位置就成為一棵不同的二叉樹。
左子樹和右子樹,也有的叫做左孩子和右孩子
二叉樹五種基本形態,方塊表示子樹

二叉樹的基本運算(不寫代碼,瞭解重點函數即可)
- 初始化
- 求雙親
- 求左孩子
- 求右孩子
- 建二叉樹
- 先序遍歷!!!
- 中序遍歷!!!
- 後序遍歷!!!
- 層次遍歷!!!
先序遍歷,中序遍歷,後序遍歷在考試中一般不要求手寫代碼,但是需要你能通過一棵樹結構,輸出最終的結果,這個博客結尾給大家看一下例題
二叉樹性質(很重要,細碎知識點很多)
性質1:二叉樹第i(i≥1)層上至多有2^i-1^個結點。
不需要死記硬背,實際需要的時候畫一個二叉樹就可以求出來了
性質2:深度為k(k≥1)的二叉樹至多有2^k^-1個結點
依舊可以推導出來
深度為1的二叉樹 結點最多為1
深度為2的二叉樹 結點最多為3
深度為3的二叉樹 結點最多為7
深度為k的二叉樹 結點最多為2^k^-1
性質3:對任何一棵二叉樹,若度數為0的結點(葉結點)個數為n~0~,度數為2的結點個數為n~2~,則n~0~ = n~2~+1
這個性質需要稍微推導一下
先回答一個問題,你知道樹的度數,怎麼計算樹的結點數
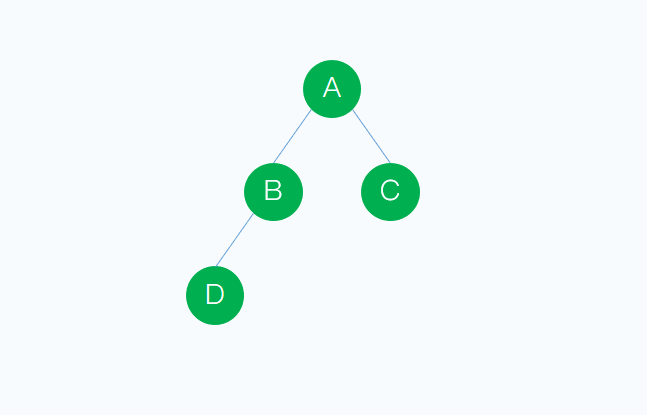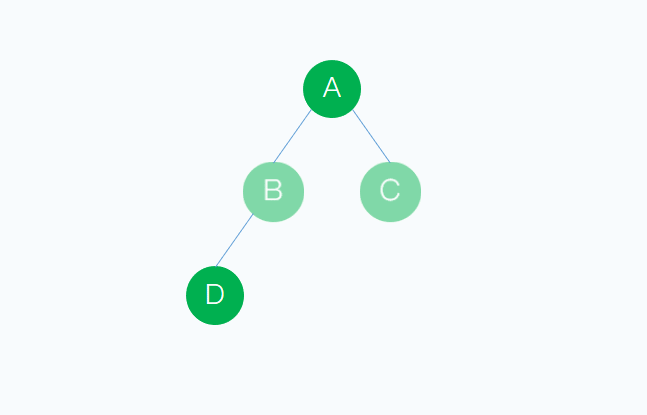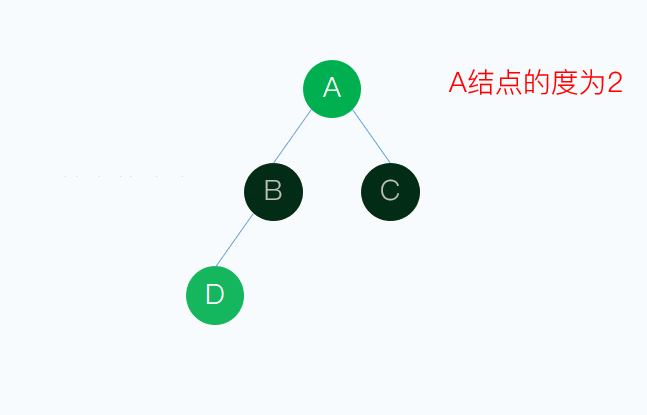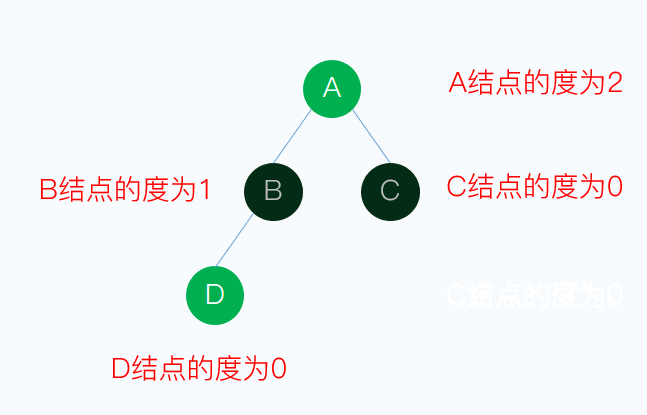
例如 樹的度數為2,結點樹為幾,這個不難想象,會出現如下情況
看到這裡不難發現,存在一個公式為 樹的度數+1=樹的結點樹
那麼我們開始推導上述公式
假設 二叉樹的0度,1度,2度結點個數為n~0~,n~1~,n~2~,結點總數為T
T = n~0~+n~1~+n~2~
樹的度數+1 = T
樹的度數怎麼求?n~0~0+n~1~1+n~2~2 是樹的度數
繼續n~0~0+n~1~1+n~2~2 +1 = T = n~0~+n~1~+n~2~
===> 2n~2~+1=n~0~+n~2~
===>n~0~=n~2~+1
好了,上述過程,爭取看明白吧
性質4:含有n個結點的完全二叉樹的深度為