【自考】數據結構第四章樹和森林，期末不掛科指南，第7篇

樹和森林

這篇博客繼續我們的《數據結構導論》課程，今天重點說說樹和森林怎麼備考自考和通過期末考試。

在開始之前，上篇博客最後其實還有一點沒有寫完，就是如何通過已知序列，恢復一棵二叉樹

看例題吧

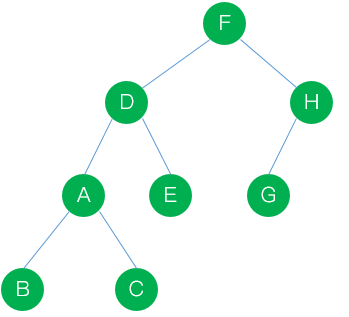
假設一棵二叉樹的中序序列與後序序列分別為：BACDEFGH 和 BCAEDGHF 建立該二叉樹

這種題目的解法，其實還是考察樹的遍歷

先看後序序列，後序序列的最後一個結點，也就是F，一定是根結點，為啥？想想吧

有根結點了，在看中序序列中 F左側的BACDE左子樹，F右側的GH右子樹

然後一遍遍的重覆這個順序，看後序序列 BCAED / GH 中，D，H是左右子樹的跟結點

看中序序列 BAC D E / G H

所以 D的左子樹 包含BAC結點，H的左子樹包含G結點，不包含右結點

剩下的就交給你自己吧，最終要實現如下圖所示即可

樹的存儲結構（該部分內容，近20年自考試卷中無涉及，過吧）

1. 孩子鏈表 表示法
2. 孩子兄弟鏈表 表示法
3. 雙親 表示法

樹、森林與二叉樹的關係

重點內容，著重掌握相互轉換

樹轉換成二叉樹

任何一棵樹可唯一地與一棵二叉樹對應。相應地，一棵二叉樹也唯一地對應一棵樹，即樹與二叉樹可以相互轉換

將樹轉換成二叉樹的方法如下

1. 將所有兄弟結點連接起來
2. 保留第一個兄弟結點與父結點的連接，斷開其他兄弟結點與父結點的連接，然後以根結點為軸心按順時針的方向旋轉45°角。

說的好繞口，其實一點都不難理解，看圖即可

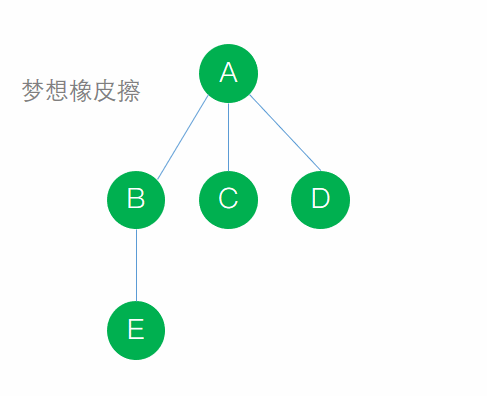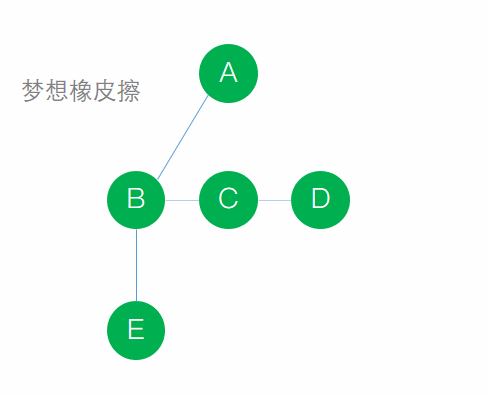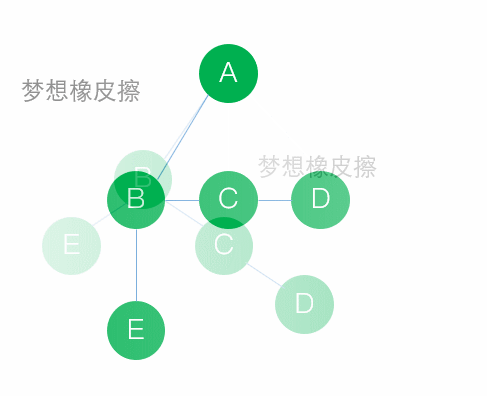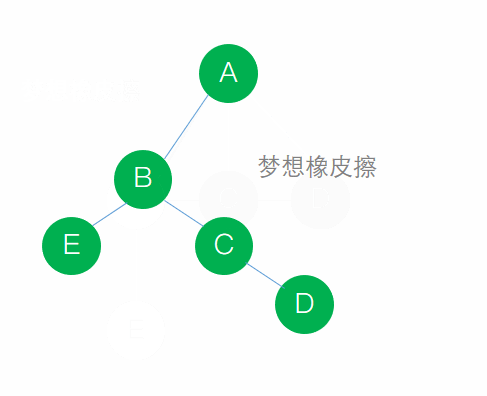
文字步驟：

1. 將BCD結點連接起來，保留A與B的連接，斷開A與C，A與D的連接
2. 按照順時針旋轉45°，C成為結點B的右孩子，D成為結點C的右孩子，E成為B的左孩子
3. 完成收工

反過去的過程也要會，也就是從二叉樹轉換成樹

森林轉換成二叉樹

方法：

1. 將每棵樹轉換成相應的二叉樹
2. 將步驟1中得到的各棵二叉樹的根結點看做是兄弟連接起來

看一個例子吧

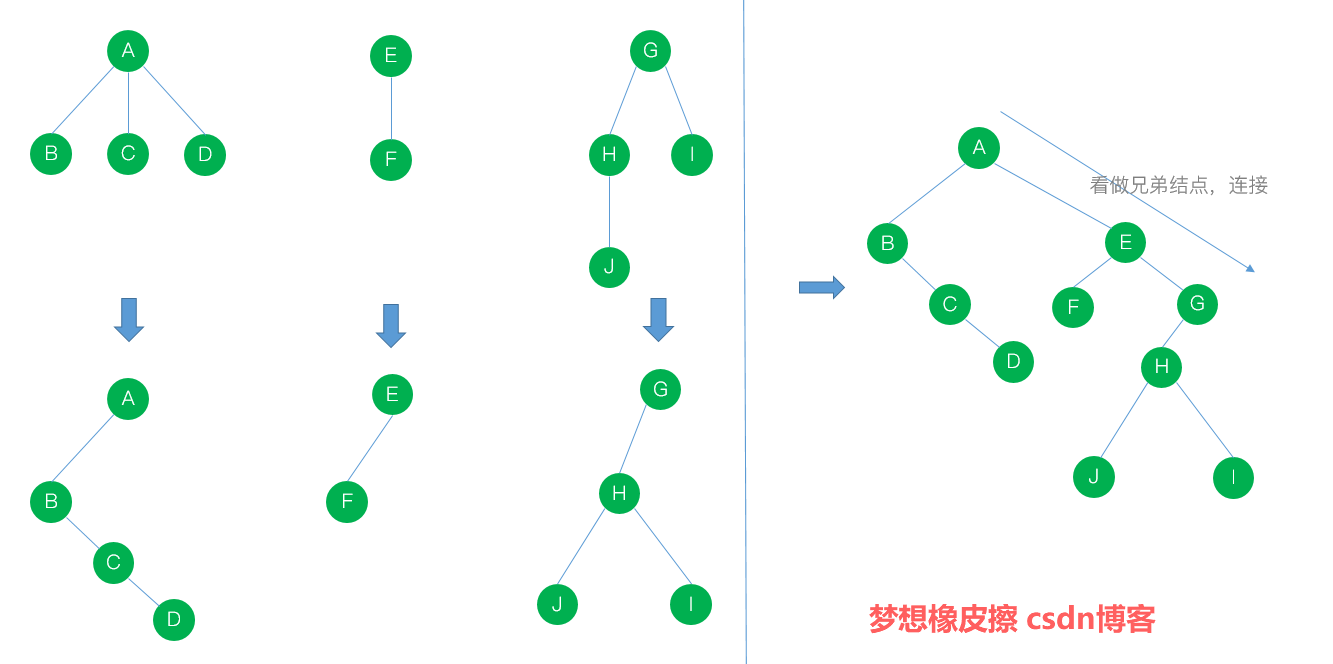
反過去的邏輯也要會，也就是從二叉樹轉換成森林

文字步驟

1. 在待轉換的二叉樹中，斷開根結點與右孩子的連線，得到兩棵二叉樹
2. 重覆斷，斷完之後還原兄弟結點到根結點即可

樹和森林的遍歷

樹的遍歷

（1）先序遍歷

1. 訪問根結點
2. 依次先序遍歷根的各棵子樹

（2）後序遍歷

1. 依次後序遍歷根的各棵子樹
2. 訪問根結點

（3）層次遍歷

1. 訪問根結點
2. 依次從左到右訪問結點

森林的遍歷

森林的遍歷有兩種方法：
（1）先序遍歷森林

1. 訪問森林中第一棵樹的根結點
2. 先序遍歷森林中第一棵樹的根結點子樹組成的森林；
3. 先序遍歷除去第一棵樹之外其餘的樹組成的森林。

（2）中序遍歷森林

1. 中序遍歷森林中第一棵樹的根結點的子樹組成的森林；
2. 訪問第一棵樹的根結點
3. 中序遍歷除去第一棵樹之外其餘的樹組成的森林。

今日小結

樹、二叉樹、森林的轉換，轉換方法蠻重要的，在自考中占比的分數一般在8分左右，所以一定要好好的練習哦~

當然有問題，可以找夢想橡皮擦

廣宣時間

更多內容，歡迎關註 https://dwz.cn/r4lCXEuL