高強度訓練第十八天總結: 二叉查找樹: 二叉查找樹就是左結點小於根節點,右結點大於根節點的一種排序樹,也叫二叉搜索樹。也叫BST,英文Binary Sort Tree。 就長下麵這弔樣 查找步驟 在二叉搜索樹b中查找x的過程為: 若b是空樹,則搜索失敗,否則: 若x等於b的根節點的數據域之值,則查找 ...
高強度訓練第十八天總結:
二叉查找樹:
二叉查找樹就是左結點小於根節點,右結點大於根節點的一種排序樹,也叫二叉搜索樹。也叫BST,英文Binary Sort Tree。
就長下麵這弔樣
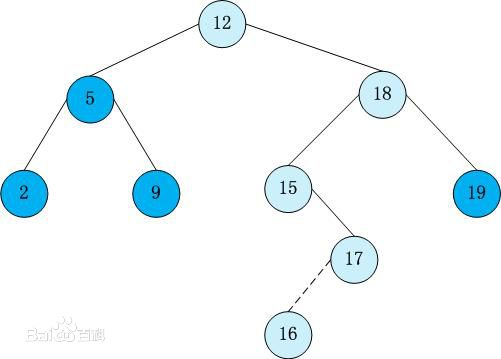
查找步驟
在二叉搜索樹b中查找x的過程為:
若b是空樹,則搜索失敗,否則:
若x等於b的根節點的數據域之值,則查找成功;否則:
若x小於b的根節點的數據域之值,則搜索左子樹;否則:
查找右子樹。
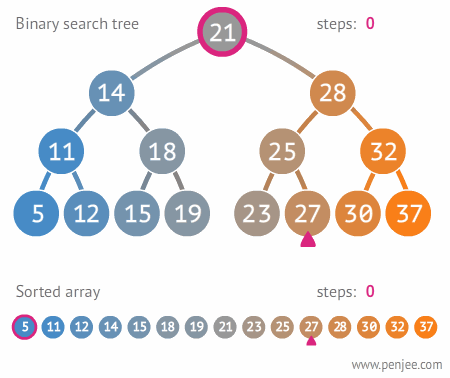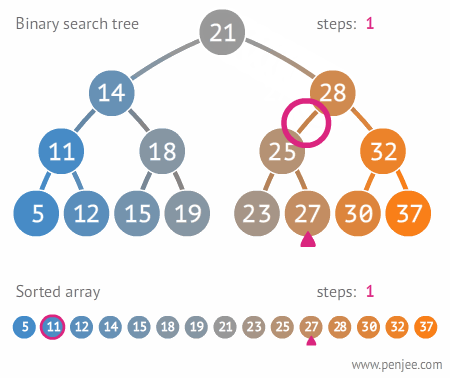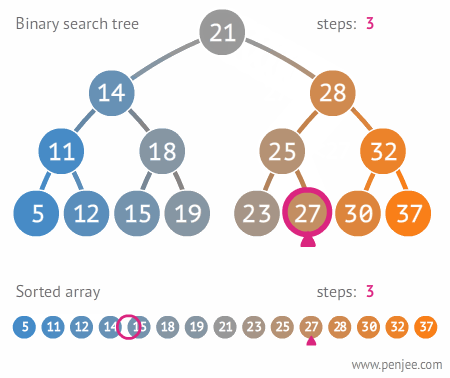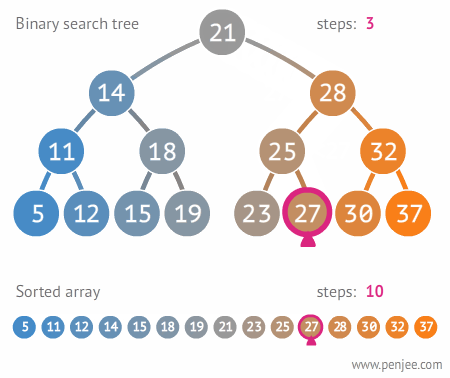
二叉搜索樹的構造
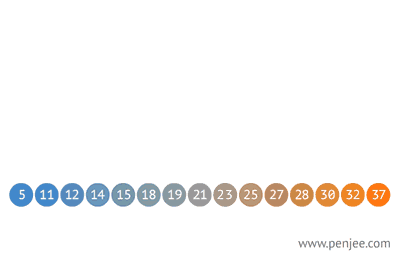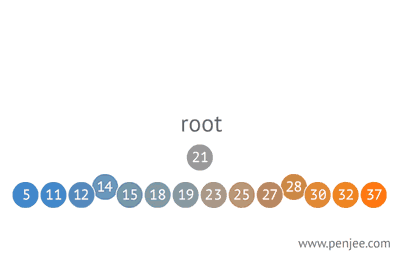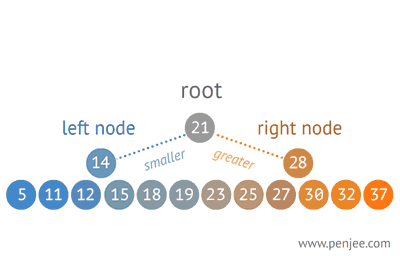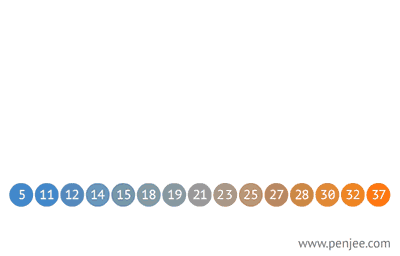
往BST中插入元素

BST轉成有序數組
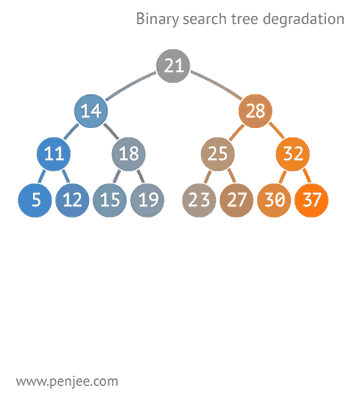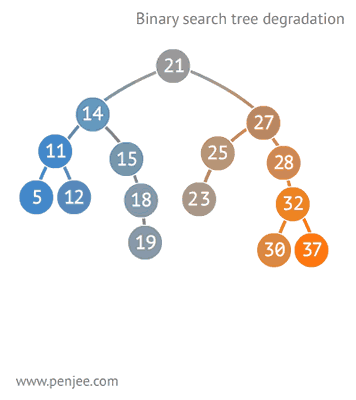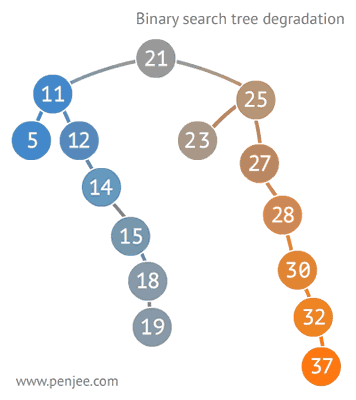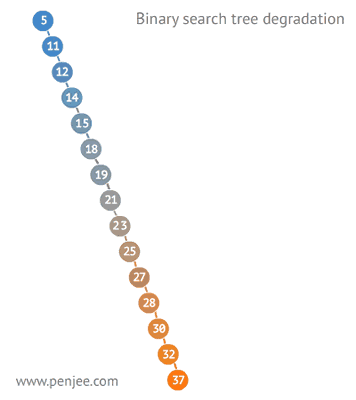
二叉查找樹比普通樹查找更快,查找、插入、刪除的時間複雜度為O(logN)。但是二叉查找樹有一種極端的情況,就是會變成一種線性鏈表似的結構。此時時間複雜度就變味了O(N),為瞭解決這種情況,出現了二叉平衡樹。
平衡二叉樹
平衡二叉樹全稱平衡二叉搜索樹,也叫AVL樹。是一種自平衡的樹。
AVL樹也規定了左結點小於根節點,右結點大於根節點。並且還規定了左子樹和右子樹的高度差不得超過1。這樣保證了它不會成為線性的鏈表。AVL樹的查找穩定,查找、插入、刪除的時間複雜度都為O(logN),但是由於要維持自身的平衡,所以進行插入和刪除結點操作的時候,需要對結點進行頻繁的旋轉。
一個有序數組被插入到平衡二叉樹
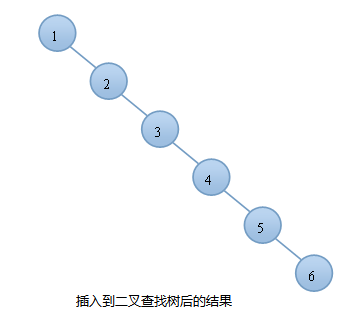
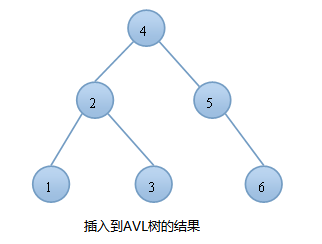
右旋
我們知道,AVL樹不僅是一顆二叉查找樹,它還有其他的性質。如果我們按照一般的二叉查找樹的插入方式可能會破壞AVL樹的平衡性。同理,在刪除的時候也有可能會破壞樹的平衡性,所以我們要做一些特殊的處理,包括:單旋轉和雙旋轉!
AVL樹的插入,單旋轉的第一種情況---右旋:
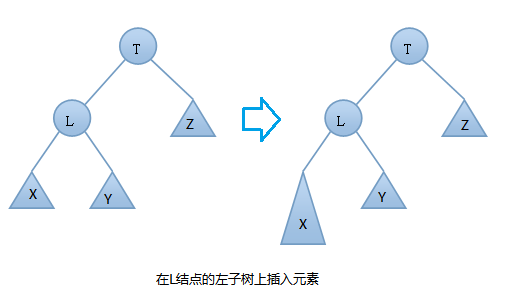
在插入之前樹是一顆AVL樹,而插入之後結點T的左右子樹高度差的絕對值不再 < 1,此時AVL樹的平衡性被破壞,我們要對其進行旋轉。由上圖可知我們是在結點T的左結點的左子樹上做了插入元素的操作,我們稱這種情況為左左情況,我們應該進行右旋轉(只需旋轉一次,故是單旋轉)。具體旋轉步驟是:
T向右旋轉成為L的右結點,同時,Y放到T的左孩子上。這樣即可得到一顆新的AVL樹,旋轉過程圖如下:
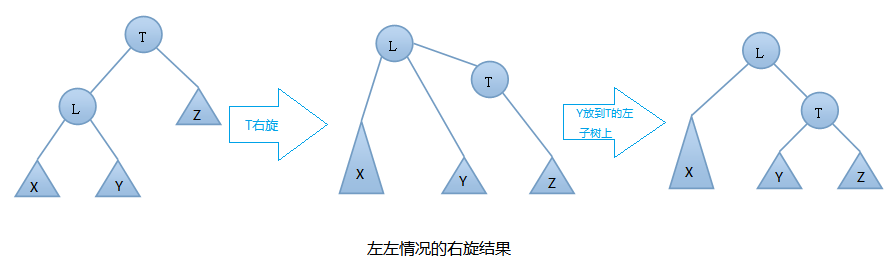
另一個:

以上就是插入操作時的單旋轉情況!我們要註意的是:誰是T誰是L,誰是R還有誰是X,Y,Z!T始終是開始不平衡的左右子樹的根節點。顯然L是T的左結點,R是T的右節點。X、Y、Y是子樹當然也可以為NULL.NULL歸NULL,但不能破壞插入時我上面所說的左左情況或者右右情況。
AVL樹的插入,雙旋轉的第一種情況---左右(先左後右)旋

我們在T結點的左結點的右子樹上插入一個元素時,會使得根為T的樹的左右子樹高度差的絕對值不再 < 1,如果只是進行簡單的右旋,得到的樹仍然是不平衡的。我們應該按照如下圖所示進行二次旋轉:
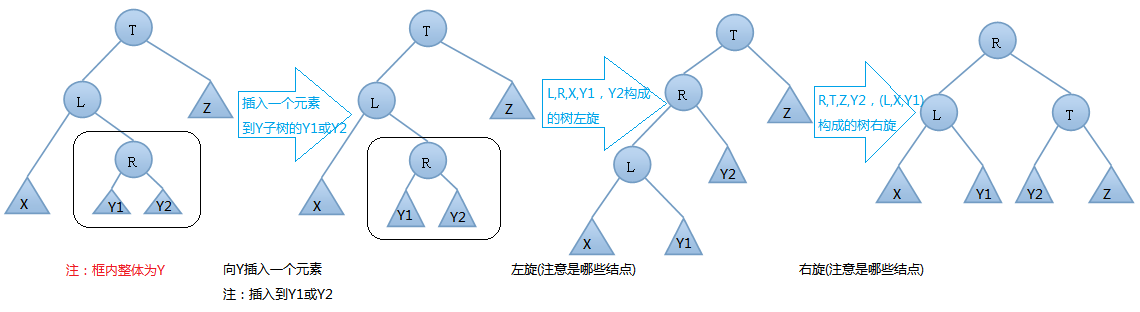
左右旋轉

AVL樹的插入,雙旋轉的第二種情況---右左(先右後左)旋:
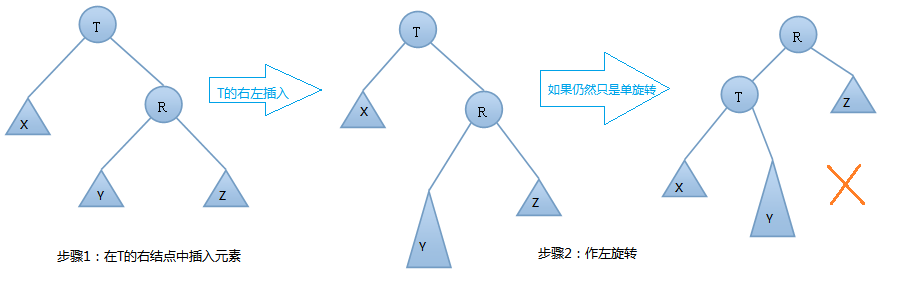
由上圖可知,我們在T結點的右結點的左子樹上插入一個元素時,會使得根為T的樹的左右子樹高度差的絕對值不再 < 1,如果只是進行簡單的左旋,得到的樹仍然是不平衡的。我們應該按照如下圖所示進行二次旋轉:
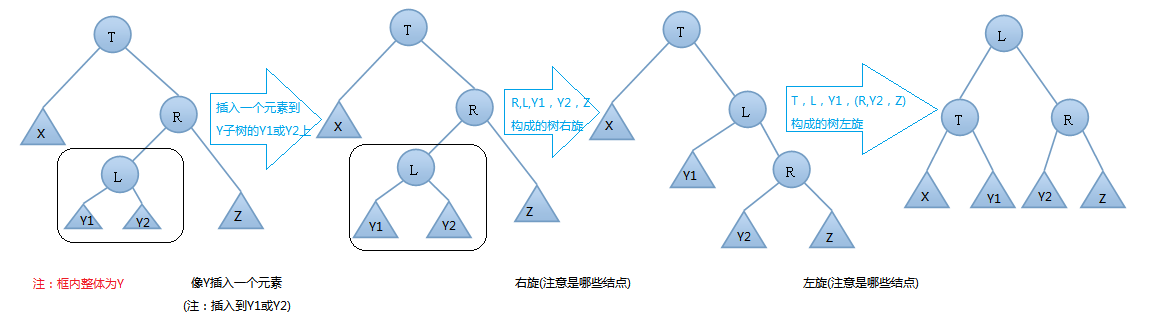
AVL樹每一個節點只能存放一個元素,並且每個節點只有兩個子節點。當進行查找時,就需要多次磁碟IO,(數據是存放在磁碟中的,每次查詢是將磁碟中的一頁數據加入記憶體,樹的每一層節點存放在一頁中,不同層數據存放在不同頁。)這樣如果需要多層查詢就需要多次磁碟IO。為瞭解決AVL樹的這個問題,就出現了B樹。但是在學B樹之前,我們需要看一下多路查找樹。
多路查找樹
多路查找樹的每一個節點的孩子樹可以多於兩個,且每個節點處可以存儲多個元素。多路查找樹是一種特殊的查找樹,所以其元素之間存在某種特定的排序關係。
2-3樹
定義2-3樹中每一個節點都具有兩個孩子(我們稱它為2節點)或三個孩子(我們稱它為3節點)。
- 一個2節點包含一個元素和兩個孩子(只能包含兩個孩子或沒有孩子,不能出現有一個孩子的情況),且與二叉排序樹類似,左子樹包含的元素小於該元素,右子樹包含的元素大於該元素。
一個3節點包含一小一大兩個元素和三個孩子(只能包含三個孩子或沒有孩子,不能出現有一個孩子或有兩個孩子的情況)。如果某個3節點有孩子,左子樹包含小於較小元素的元素,右子樹包含大於較大元素的元素,中間子樹包含介於兩元素之間的元素。
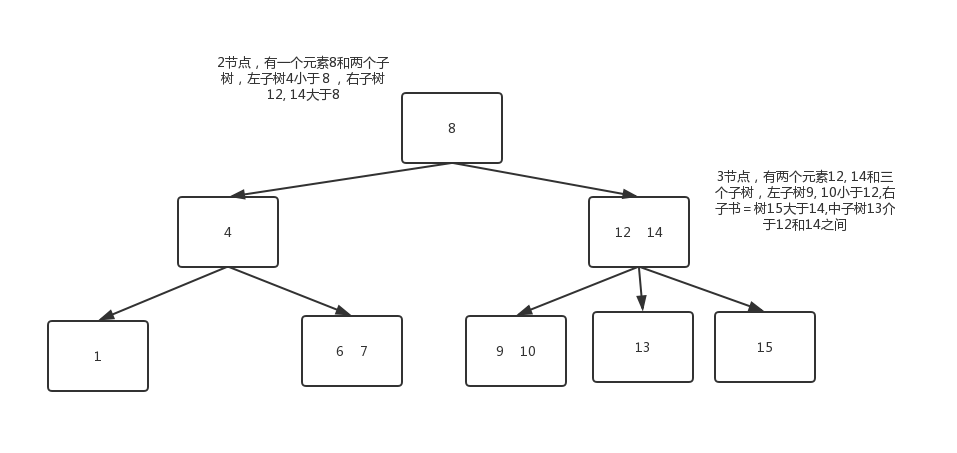
一顆完美平衡的2-3查找樹中的所有空鏈接到根結點的距離都是相同的。查找
要判斷查找的鍵值是否在樹中,我們先將它和根結點中的鍵比較。如果它和其中的任何一個相等,查找命中。否則我們就根據比較的結果找到指向相應區間的鏈接,併在其指向的子樹中遞歸地繼續查找。如果這是個空鏈接,查找未命中。
2-3樹的插入實現
要在2-3樹中插入一個新結點,我們可以和二叉查找樹一樣先進行一次未命中的查找,然後把新結點掛在樹的底部。但這樣的話樹無法保持完美平衡性。我們使用2-3樹的主要原因就在於它能夠在插入之後繼續保持平衡。
2-3樹插入可以分為三種情況
- 對於空樹,插入一個2節點即可
- 插入節點到一個2節點的葉子上
由於其本身只有一個元素,所以只需要將其升級為3節點即可。
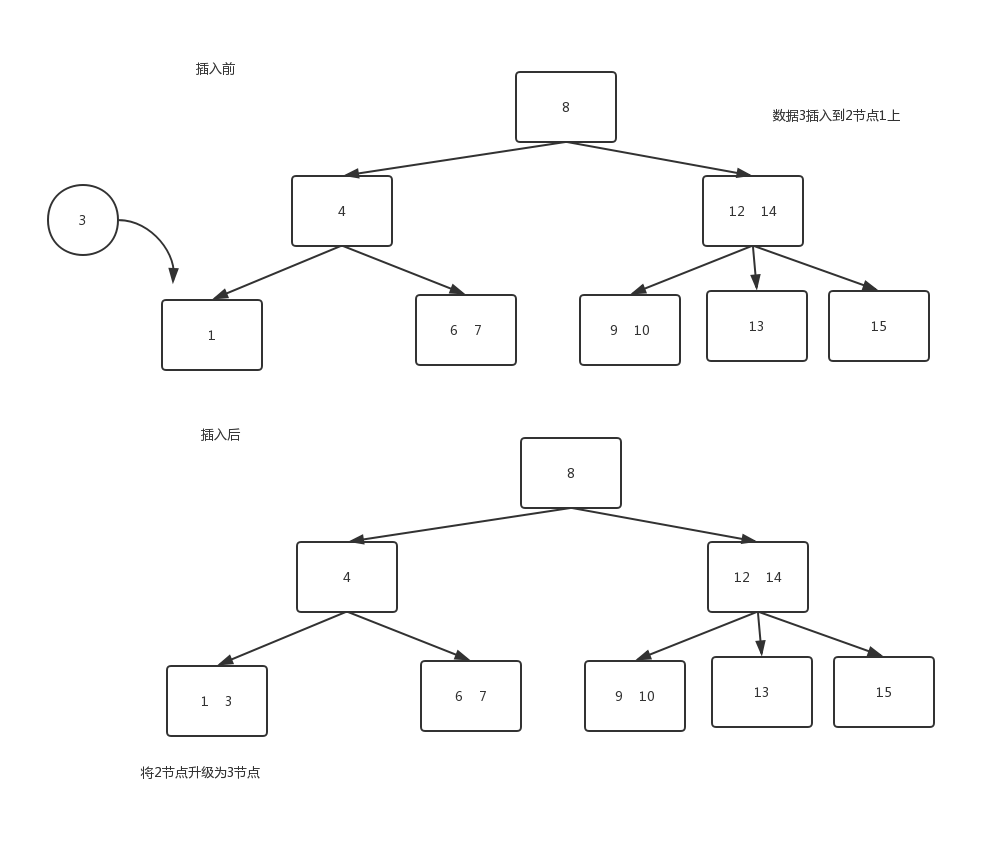
往3節點中插入一個新數據
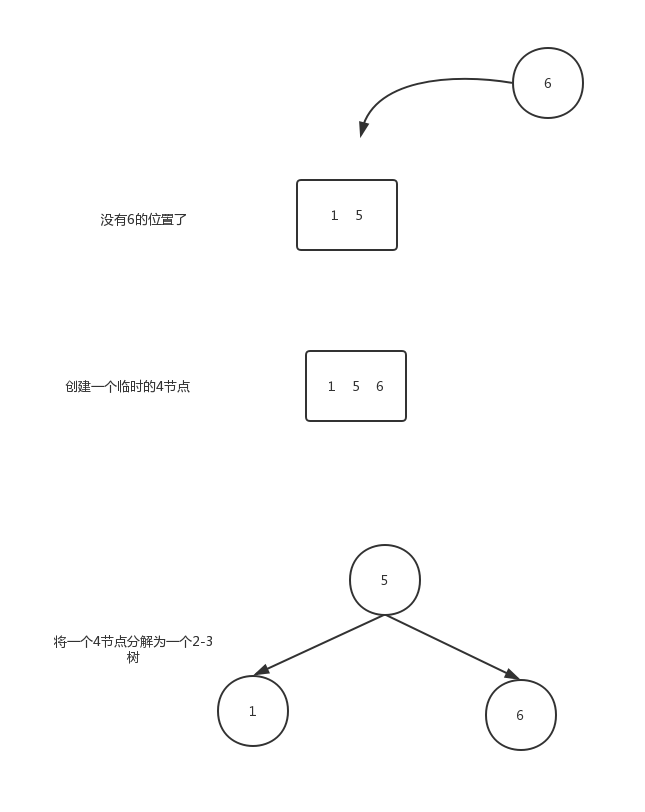
因為3節點本省就是2-3樹的最大容量(已經有兩個元素),因此需要拆分。分情況討論如下所示:只有一個3-結點的樹,向其插入一個新鍵
這棵樹唯一的結點中已經沒有可插入的空間了。我們又不能把新鍵插在其空結點上(破壞了完美平衡)。為了將新鍵插入,我們先臨時將新鍵存入該結點中,使之成為一個4-結點。創建一個4-結點很方便,因為很容易將它轉換為一顆由3個2-結點組成的2-3樹(如圖所示),這棵樹既是一顆含有3個結點的二叉查找樹,同時也是一顆完美平衡的2-3樹,其中所有空鏈接到根結點的距離都相等
向一個父節點為2節點的3節點中插入數據
假設未命中的查找結束於一個3-結點,而它的父結點是一個2-結點。在這種情況下我們需要在維持樹的完美平衡的前提下為新鍵騰出空間。
我們先像剛纔一樣構造一個臨時的4-結點並將其分解,但此時我們不會為中鍵創建一個新結點,而是將其移動至原來的父結點中。

這次轉換並沒有影響2-3樹的主要性質,樹仍然是有序的,因為中鍵被移動到父節點中去了。向一個父節點為3節點的3節點中插入數據
假設未命中的查找結束於一個3-結點,而它的父結點是一個3-結點。
我們再次和剛纔一樣構造一個臨時的4-結點並分解它,然後將它的中鍵插入它的父結點中。但父結點也是一個3-結點,因此我們再用這個中鍵構造一個新的臨時4-結點,然後在這個結點上進行相同的變換,即分解這個父結點並將它的中鍵插入到它的父結點中去。
我們就這樣一直向上不斷分解臨時的4-結點並將中鍵插入更高的父結點,直至遇到一個2-結點並將它替換為一個不需要繼續分解的3-結點,或者是到達3-結點的根。
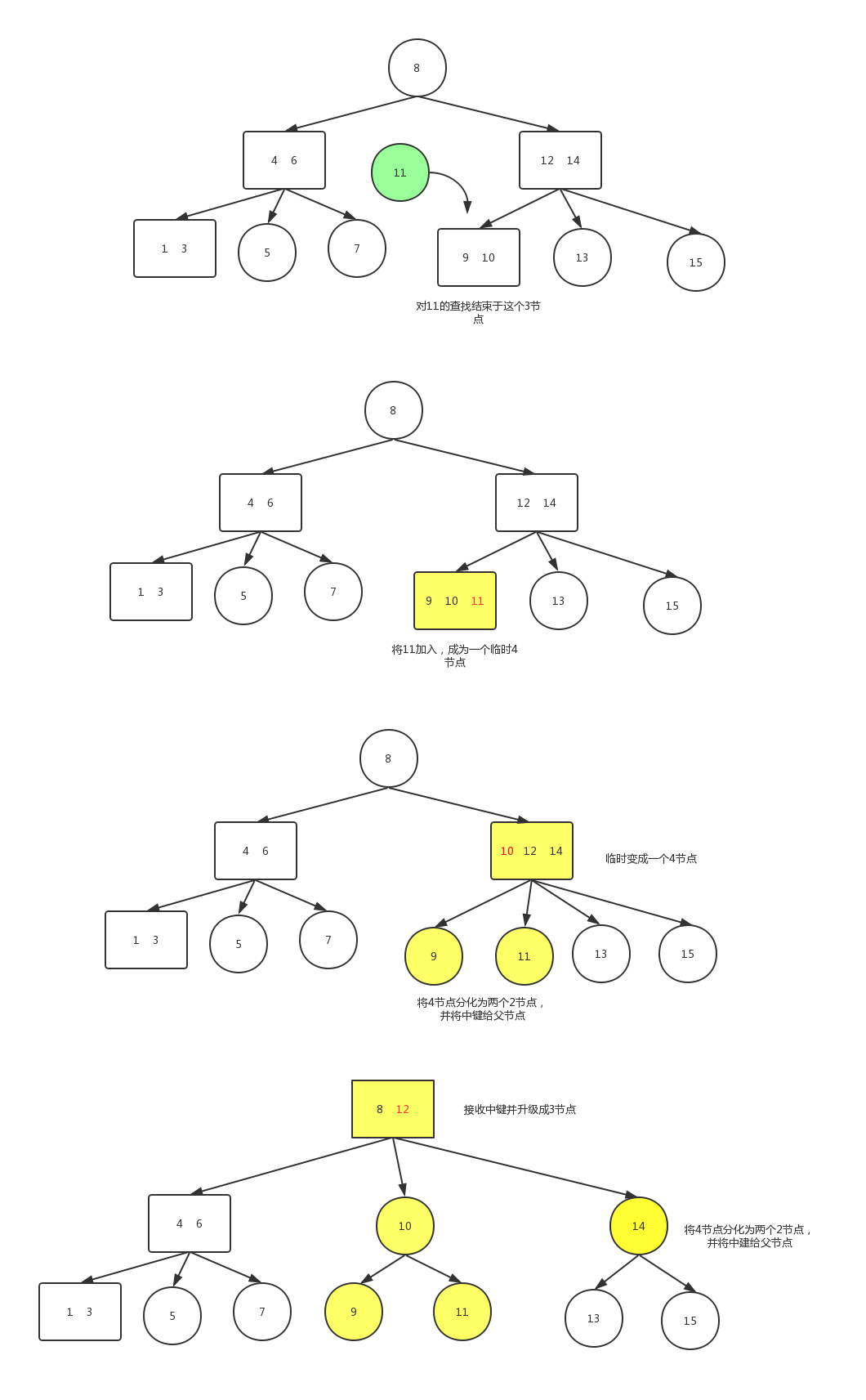
B樹(Blance-Tree)
B樹,在寫法上通常是B-樹,這不是減號的意思,只是一種表達方式,它是一種能夠存儲數據、對數據進行排序並允許以O(log n)的時間複雜度運行進行查找、順序讀取、插入和刪除的數據結構。,概括來說是一個節點可以擁有多於2個節點的二叉查找樹。
一個m階的B樹具有如下特點:
- B樹根節點至少有兩個節點,每個節點可以有多個子樹
- 每個中間節點都包含k-1個元素和k個子樹,其中 m/2 ⇐ k ⇐ m
- 所有的葉子結點都位於同一層
- 每個節點中的元素從小到大排列,節點當中k-1個元素正好是k個孩子包含的元素的值域分劃。
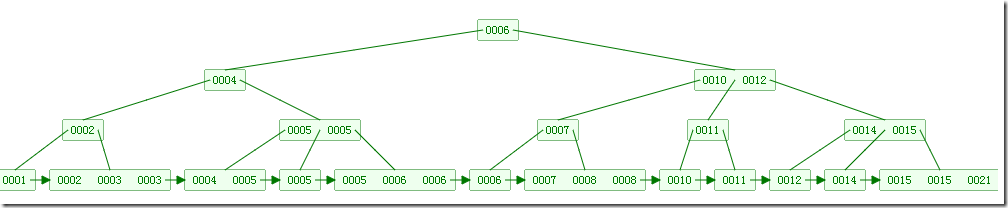
看概念還是挺晦澀的,直接放張圖看看正宗的B樹
5.每個節點中的元素從小到大排列,節點當中k-1個元素正好是k個孩子包含的元素的值域分劃。

插入數據
插入的數據依次是6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4
,效果圖如下:

B+樹
B+樹是對B樹的一種變形樹,它與B樹的差異在於:
- 有k個子結點的結點必然有k個關鍵碼;
- 非葉結點僅具有索引作用,跟記錄有關的信息均存放在葉結點中。
- 樹的所有葉結點構成一個有序鏈表,可以按照關鍵碼排序的次序遍歷全部記錄。
插入數據如下所示:

B和B+樹的區別在於,B+樹的非葉子結點只包含導航信息,不包含實際的值,所有的葉子結點和相連的節點使用鏈表相連,便於區間查找和遍歷。
B+ 樹的優點在於:
- 由於B+樹在內部節點上不好含數據信息,因此在記憶體頁中能夠存放更多的key。 數據存放的更加緊密,具有更好的空間局部性。因此訪問葉子幾點上關聯的數據也具有更好的緩存命中率。
- B+樹的葉子結點都是相鏈的,因此對整棵樹的便利只需要一次線性遍歷葉子結點即可。而且由於數據順序排列並且相連,所以便於區間查找和搜索。而B樹則需要進行每一層的遞歸遍歷。相鄰的元素可能在記憶體中不相鄰,所以緩存命中性沒有B+樹好。
但是B樹也有優點,其優點在於,由於B樹的每一個節點都包含key和value,因此經常訪問的元素可能離根節點更近,因此訪問也更迅速。下麵是B 樹和B+樹的區別圖:
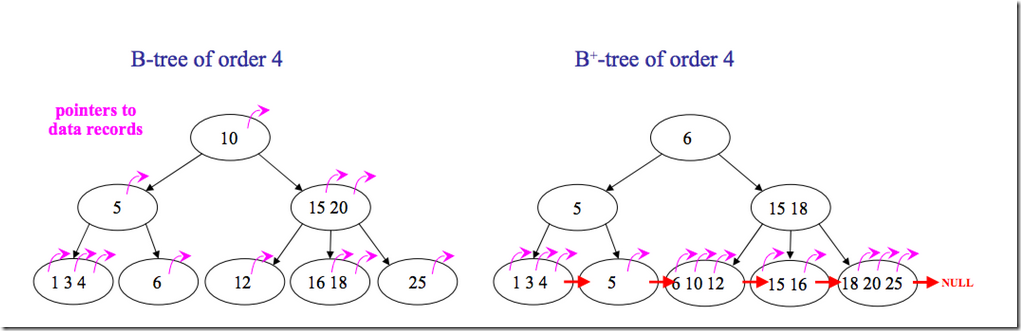
為什麼說B+樹比B樹更適合資料庫索引?
B+樹的磁碟讀寫代價更低:B+樹的內部節點並沒有指向關鍵字具體信息的指針,因此其內部節點相對B樹更小,如果把所有同一內部節點的關鍵字存放在同一盤塊中,那麼盤塊所能容納的關鍵字數量也越多,一次性讀入記憶體的需要查找的關鍵字也就越多,相對IO讀寫次數就降低了。
B+樹的查詢效率更加穩定:由於非終結點並不是最終指向文件內容的結點,而只是葉子結點中關鍵字的索引。所以任何關鍵字的查找必須走一條從根結點到葉子結點的路。所有關鍵字查詢的路徑長度相同,導致每一個數據的查詢效率相當。
由於B+樹的數據都存儲在葉子結點中,分支結點均為索引,方便掃庫,只需要掃一遍葉子結點即可,但是B樹因為其分支結點同樣存儲著數據,我們要找到具體的數據,需要進行一次中序遍歷按序來掃,所以B+樹更加適合在區間查詢的情況,所以通常B+樹用於資料庫索引。
B樹在提高了IO性能的同時並沒有解決元素遍歷的我效率低下的問題,正是為瞭解決這個問題,B+樹應用而生。B+樹只需要去遍歷葉子節點就可以實現整棵樹的遍歷。而且在資料庫中基於範圍的查詢是非常頻繁的,而B樹不支持這樣的操作或者說效率太低。
紅黑樹:
紅黑樹也叫RB樹,RB-Tree。是一種自平衡的二叉查找樹,它的節點的顏色為紅色和黑色。它不嚴格控制左、右子樹高度或節點數之差小於等於1。也是一種解決二叉查找樹極端情況的數據結構。
紅黑樹規定了:
節點是紅色或黑色。
根節點是黑色。
每個葉子節點都是黑色的空節點(NIL節點)。
每個紅色節點的兩個子節點都是黑色。也就是說從每個葉子到根的所有路徑上不能有兩個連續的紅色節點)。
從任一節點到其每個葉子的所有路徑都包含相同數目的黑色節點。
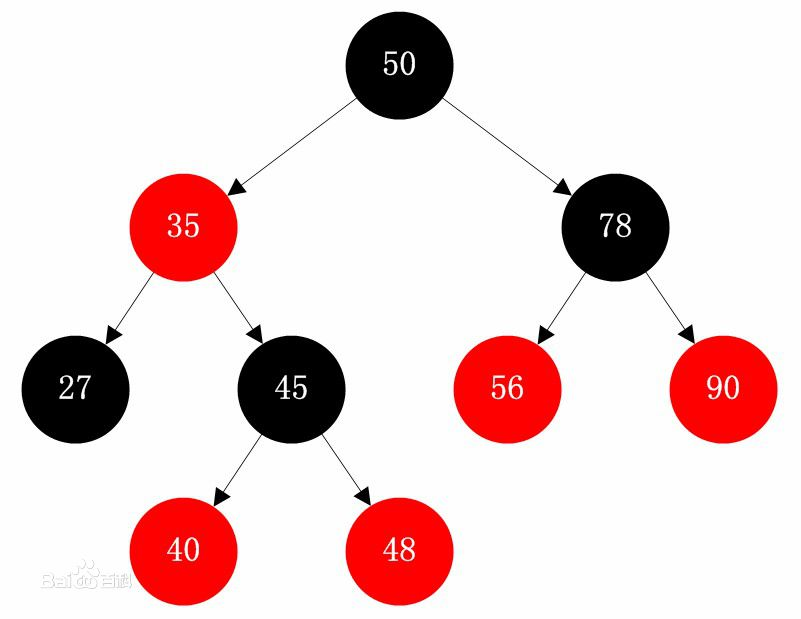
紅黑樹在查找方面和AVL樹操作幾乎相同。但是在插入和刪除操作上,AVL樹每次插入刪除會進行大量的平衡度計算,紅黑樹是犧牲了嚴格的高度平衡的優越條件為代價,它只要求部分地達到平衡要求,結合變色,降低了對旋轉的要求,從而提高了性能。紅黑樹能夠以O(log2 n)的時間複雜度進行搜索、插入、刪除操作。此外,由於它的設計,任何不平衡都會在三次旋轉之內解決。
相比於BST,因為紅黑樹可以能確保樹的最長路徑不大於兩倍的最短路徑的長度,所以可以看出它的查找效果是有最低保證的。在最壞的情況下也可以保證O(logN)的,這是要好於二叉查找樹的。因為二叉查找樹最壞情況可以讓查找達到O(N)。
紅黑樹的演算法時間複雜度和AVL相同,但統計性能比AVL樹更高,所以在插入和刪除中所做的後期維護操作肯定會比紅黑樹要耗時好多,但是他們的查找效率都是O(logN),所以紅黑樹應用還是高於AVL樹的. 實際上插入 AVL 樹和紅黑樹的速度取決於你所插入的數據.如果你的數據分佈較好,則比較宜於採用 AVL樹(例如隨機產生系列數),但是如果你想處理比較雜亂的情況,則紅黑樹是比較快的。
紅黑樹廣泛用於TreeMap、TreeSet,以及jdk1.8後的HashMap(hash衝突鏈表超過8就轉換成紅黑樹)。
參考:
https://www.cnblogs.com/jiqing9006/p/5873097.html
https://blog.csdn.net/wanderlustLee/article/details/81297253
https://www.cnblogs.com/zhuwbox/p/3636783.html
https://www.cnblogs.com/lishanlei/p/10707791.html
https://www.cnblogs.com/yangecnu/p/Introduce-B-Tree-and-B-Plus-Tree.html



