前面幾篇隨筆中介紹了利用矩陣乘法(特別是應用快速冪運算)解決遞推快速求值、置換和幾何變換等問題的方法。實際上矩陣乘法的應用遠不止這些,下麵通過幾個實例來介紹下矩陣乘法的其它一些典型的應用。 【例1】多少條道。 給定一個有向圖,問從A點恰好走k步(允許重覆經過邊)到達B點的方案數mod p的值。 (1 ...
前面幾篇隨筆中介紹了利用矩陣乘法(特別是應用快速冪運算)解決遞推快速求值、置換和幾何變換等問題的方法。實際上矩陣乘法的應用遠不止這些,下麵通過幾個實例來介紹下矩陣乘法的其它一些典型的應用。
【例1】多少條道。
給定一個有向圖,問從A點恰好走k步(允許重覆經過邊)到達B點的方案數mod p的值。
(1)編程思路。
本題是矩陣乘法應用在圖論中的一個典型方法。
給定了有向圖,可以得到該圖的鄰接矩陣A,在鄰接矩陣A中,A(i,j)=1當且僅當存在一條邊i->j。若i->j不存在直接相連接的邊,則A(i,j)=0。
令C=A*A,那麼 C(i,j)= ΣA(i,k)*A(k,j),實際上就等於從點i到點j恰好經過2條邊的路徑數(k為中轉點)。
類似地,C*A =A*A*A的第i行第j列就表示從i到j經過3條邊的路徑數。同理,如果要求經過k步的路徑數,只需要採用快速冪運算求出A^k即可。
(2)源程式。
#include <stdio.h>
#include <string.h>
#define MOD 1000
struct Matrix
{
int mat[21][21]; // 存儲矩陣中各元素
};
Matrix matMul(Matrix a ,Matrix b,int n,int m)
{
Matrix c;
memset(c.mat,0,sizeof(c.mat));
int i,j,k;
for (k = 1; k<=n ; k++)
for (i=1 ;i<=n ; i++)
if (a.mat[i][k]!=0)
for (j = 1 ;j<=n ;j++)
c.mat[i][j] = (c.mat[i][j] + a.mat[i][k] * b.mat[k][j]) % m;
return c;
}
Matrix quickMatPow(Matrix a ,int n,int b,int m) // n階矩陣a快速b次冪
{
Matrix c;
memset(c.mat ,0 ,sizeof(c.mat));
int i;
for (i = 1 ;i <= n ;i++)
c.mat[i][i] = 1;
while (b!=0)
{
if (b & 1)
c = matMul(c ,a ,n,m); // c=c*a;
a = matMul(a ,a ,n,m); // a=a*a
b /= 2;
}
return c;
}
int main()
{
int n,m,s,t,nCase,a,b,k,i;
Matrix p,ans;
while (scanf("%d%d",&n,&m) && n+m!=0)
{
memset(p.mat,0,sizeof(p.mat));
for (i=1;i<=m;i++)
{
scanf("%d%d",&s,&t);
p.mat[s+1][t+1]=1;
}
scanf("%d",&nCase);
for (i=1;i<=nCase;i++)
{
scanf("%d%d%d",&a,&b,&k);
ans=quickMatPow(p,n,k,MOD);
printf("%d\n" ,ans.mat[a+1][b+1]);
}
}
return 0;
}
將此源程式提交給 HDU 2157 “How many ways??”,可以Accepted。
我們知道,構造好平移、縮放或旋轉的轉換矩陣後,可以實現幾何變換;構造好置換矩陣後,可以實現置換操作。這樣,在一些問題中,我們也可以根據狀態變化的情況,構造一個狀態轉移矩陣,來解決一些狀態變換類問題。
【例2】燈的狀態。
有n盞燈排成一排,開關狀態已知,0代表燈熄滅,1代表點亮。每過一秒:第i(1<=i<=n)盞燈會根據剛纔左邊的那個燈的開關情況變化,如果左邊的燈是亮的,它就會變化,如果左邊的燈是熄滅的,它就保持原來狀態。第1盞燈的左邊是最後一盞燈。問m秒後全部n盞燈的狀態。
(1)編程思路。
設f[i]代表第i盞燈的狀態,f[i]=1代表第i盞燈是點亮的,f[i]=0代表第i盞燈是熄滅的。
對於第i(1<i<=n)盞燈,若第i-1盞燈點亮的: 當前燈的動作: 1->0; 0->1;
若第i-1盞燈熄滅的: 當前燈的動作: 1->1; 0->0;
由此,可推得 f[i]=(f[i]+f[i-1])%2 (1<i<=n)。
對於第1盞燈,它的狀態變化與第n盞燈相關,即 f[1]=(f[1]+f[n])%2 。
由此,我們可以構造一個n*n的狀態轉移矩陣P來完成燈的狀態轉換。

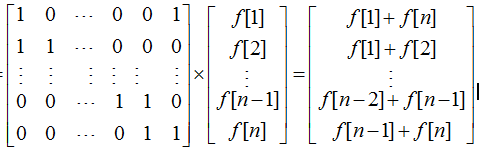
構造好狀態轉移矩陣P,P^m的結果就是m秒後的狀態轉移矩陣。再將狀態轉移矩陣除以n盞燈初始狀態列向量F即可得到n盞燈的最終狀態。
(2)源程式。
#include <stdio.h>
#include <string.h>
#define MOD 2
struct Matrix
{
int mat[101][101]; // 存儲矩陣中各元素
};
Matrix matMul(Matrix a ,Matrix b,int n)
{
Matrix c;
memset(c.mat,0,sizeof(c.mat));
int i,j,k;
for (k = 1; k<=n ; k++)
for (i=1 ;i<=n ; i++)
if (a.mat[i][k]!=0)
for (j = 1 ;j<=n ;j++)
c.mat[i][j] = (c.mat[i][j] + a.mat[i][k] * b.mat[k][j]) % MOD;
return c;
}
Matrix quickMatPow(Matrix a ,int n,int b) // n階矩陣a快速b次冪
{
Matrix c;
memset(c.mat ,0 ,sizeof(c.mat));
int i;
for (i = 1 ;i <= n ;i++)
c.mat[i][i] = 1;
while (b!=0)
{
if (b & 1)
c = matMul(c ,a ,n); // c=c*a;
a = matMul(a ,a ,n); // a=a*a
b /= 2;
}
return c;
}
int main()
{
int m,n,i,j,s;
char f[101];
int temp[101],ans[101];
Matrix p;
while(scanf("%d" ,&m)!=EOF)
{
scanf("%s",f);
n=strlen(f);
for (i=1;i<=n;i++)
temp[i]=f[i-1]-'0';
memset(p.mat,0,sizeof(p.mat));
p.mat[1][1]=p.mat[1][n]=1;
for (i=2;i<=n;i++)
p.mat[i][i-1]=p.mat[i][i]=1;
p = quickMatPow(p,n,m);
for (i=1;i<=n;i++)
{
s=0;
for (j=1;j<=n;j++)
s+=p.mat[i][j]*temp[j];
ans[i]=s%MOD;
}
for (i=1;i<=n;i++)
printf("%d" ,ans[i]);
printf("\n");
}
return 0;
}
將此源程式提交給 HDU 2276 “Kiki & Little Kiki 2”,可以Accepted。
【例3】訓練小貓。
用k個操作序列來訓練n只小貓。 操作系列中:
g i:表示第i只貓得到一個花生, e i :表示第i只貓吃掉所有花生,s i j :表示第i只貓和第j只貓交換花生。
k個操作序列要被重覆m次,問最後每隻貓有多少花生。
(1)編程思路。
構造一個(n+1)*(n+1)(下標從1開始)的轉換矩陣P,該轉換矩陣根據K個操作序列來構造,具體構造方法是:
先將P初始化為單位矩陣。
對於g i操作,將當前矩陣P的第i行的第(n+1)列加1。
例如,有3只小貓,某次操作前3只小貓的花生數分別為x,y和z。 執行 g 2 操作。矩陣的構造表示為
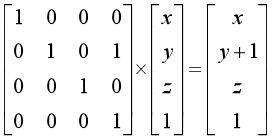
對於 e i 操作:將當前矩陣P第i行全部清0即可。
對於 s i j 操作 :交換當前矩陣P的第i行和第j行即可。
構造好了轉換矩陣(註意該轉換矩陣代表著一次k個操作序列),執行P^m,相當將k個操作序列重覆m次。
由於n只小貓的初始花生數均為0,因此最終P矩陣的第n+1列的第1~n行元素的值就是最後n只小貓的最後花生數。
(2)源程式。
#include <stdio.h>
#include <string.h>
struct Matrix
{
__int64 mat[105][105];
};
Matrix start;
Matrix matMul(Matrix a ,Matrix b,int n)
{
Matrix c;
memset(c.mat,0,sizeof(c.mat));
int i,j,k;
for (k = 1; k<=n ; k++)
for (i=1 ;i<=n ; i++)
if(a.mat[i][k])
for (j = 1 ;j<=n ;j++)
c.mat[i][j] = (c.mat[i][j] + a.mat[i][k] * b.mat[k][j]);
return c;
}
Matrix quickMatPow(Matrix a ,int b ,int n) // n階矩陣a快速b次冪
{
Matrix c;
memset(c.mat ,0 ,sizeof(c.mat));
int i;
for (i = 1 ;i <= n ;i++)
c.mat[i][i] = 1;
while(b)
{
if (b & 1)
c = matMul(c ,a ,n); // c=c*a;
a = matMul(a ,a ,n); // a=a*a
b /= 2;
}
return c;
}
int main()
{
int n,m,k,i,j;
__int64 t;
while (scanf("%d%d%d",&n,&m,&k)!=EOF)
{
if (n==0 && m==0 && k==0)
break;
n++;
memset(start.mat, 0, sizeof(start.mat));
for (i = 1; i<=n; i++)
start.mat[i][i] = 1;
for (i=1; i<=k; i++)
{
int a, b;
char ch[2];
scanf("%s", ch);
if (ch[0] == 'g')
{
scanf("%d", &a);
start.mat[a][n]++;
}
else if (ch[0] == 'e')
{
scanf("%d", &a);
for (j = 1; j <= n; j++)
start.mat[a][j] = 0;
}
else
{
scanf("%d%d", &a, &b);
for (j = 1; j<=n; j++)
{
t=start.mat[a][j];
start.mat[a][j]=start.mat[b][j];
start.mat[b][j]=t;
}
}
}
start= quickMatPow(start,m,n);
for (i = 1; i <n; i++)
printf("%I64d ", start.mat[i][n]);
printf("\n");
}
return 0;
}
將此源程式提交給 POJ 3735“Training little cats”,可以Accepted。



