1.一個問題 InnoDB一棵B+樹可以存放多少行數據?這個問題的簡單回答是:約2千萬。為什麼是這麼多呢?因為這是可以算出來的,要搞清楚這個問題,我們先從InnoDB索引數據結構、數據組織方式說起。 我們都知道電腦在存儲數據的時候,有最小存儲單元,這就好比我們今天進行現金的流通最小單位是一毛。在計 ...
1.一個問題
InnoDB一棵B+樹可以存放多少行數據?這個問題的簡單回答是:約2千萬。為什麼是這麼多呢?因為這是可以算出來的,要搞清楚這個問題,我們先從InnoDB索引數據結構、數據組織方式說起。
我們都知道電腦在存儲數據的時候,有最小存儲單元,這就好比我們今天進行現金的流通最小單位是一毛。在電腦中磁碟存儲數據最小單元是扇區,一個扇區的大小是512位元組,而文件系統(例如XFS/EXT4)他的最小單元是塊,一個塊的大小是4k,而對於我們的InnoDB存儲引擎也有自己的最小儲存單元——頁(Page),一個頁的大小是16K。
下麵幾張圖可以幫你理解最小存儲單元:
文件系統中一個文件大小隻有1個位元組,但不得不占磁碟上4KB的空間。

innodb的所有數據文件(尾碼為ibd的文件),他的大小始終都是16384(16k)的整數倍。
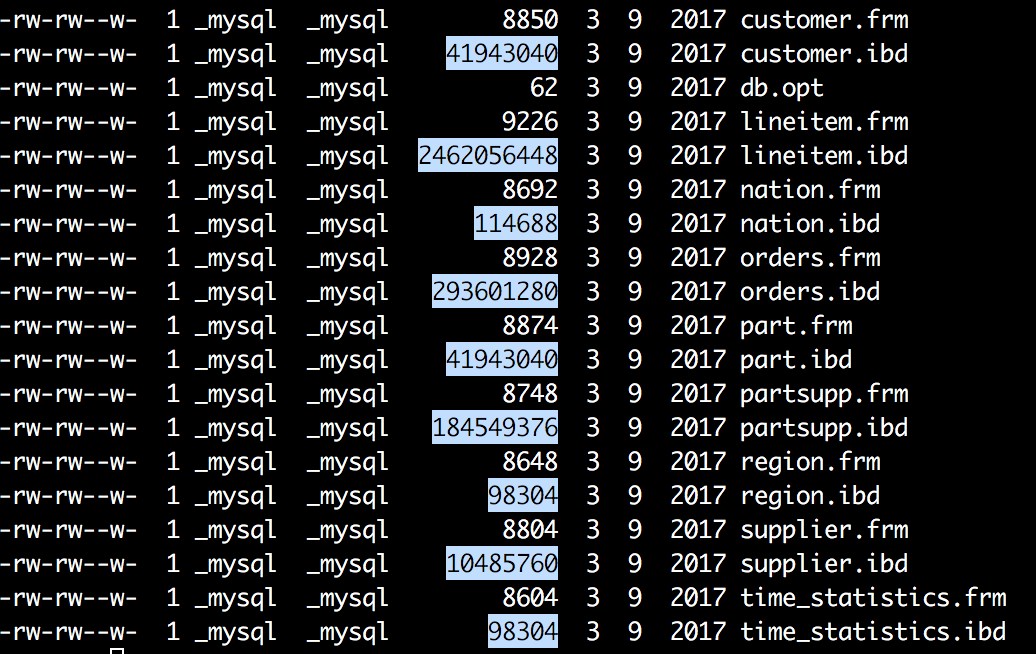
磁碟扇區、文件系統、InnoDB存儲引擎都有各自的最小存儲單元。
在MySQL中我們的InnoDB頁的大小預設是16k,當然也可以通過參數設置:
mysql> show variables like 'innodb_page_size';
+------------------+-------+
| Variable_name | Value |
+------------------+-------+
| innodb_page_size | 16384 |
+------------------+-------+
1 row in set (0.00 sec)數據表中的數據都是存儲在頁中的,所以一個頁中能存儲多少行數據呢?假設一行數據的大小是1k,那麼一個頁可以存放16行這樣的數據。
如果資料庫只按這樣的方式存儲,那麼如何查找數據就成為一個問題,因為我們不知道要查找的數據存在哪個頁中,也不可能把所有的頁遍歷一遍,那樣太慢了。所以人們想了一個辦法,用B+樹的方式組織這些數據。如圖所示:
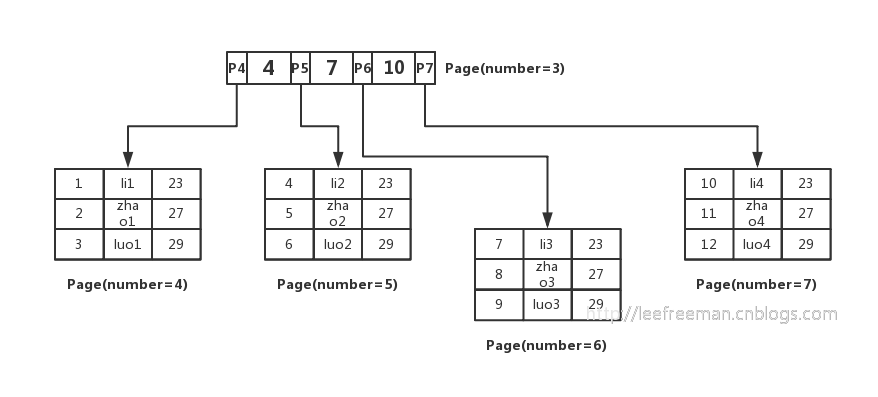
我們先將數據記錄按主鍵進行排序,分別存放在不同的頁中(為了便於理解我們這裡一個頁中只存放3條記錄,實際情況可以存放很多),除了存放數據的頁以外,還有存放鍵值+指針的頁,如圖中page number=3的頁,該頁存放鍵值和指向數據頁的指針,這樣的頁由N個鍵值+指針組成。當然它也是排好序的。這樣的數據組織形式,我們稱為索引組織表。現在來看下,要查找一條數據,怎麼查?
如select * from user where id=5;
這裡id是主鍵,我們通過這棵B+樹來查找,首先找到根頁,你怎麼知道user表的根頁在哪呢?其實每張表的根頁位置在表空間文件中是固定的,即page number=3的頁(這點我們下文還會進一步證明),找到根頁後通過二分查找法,定位到id=5的數據應該在指針P5指向的頁中,那麼進一步去page number=5的頁中查找,同樣通過二分查詢法即可找到id=5的記錄:
中,那麼進一步去page number=5的頁中查找,同樣通過二分查詢法即可找到id=5的記錄:
5|zhao2|27現在我們清楚了InnoDB中主鍵索引B+樹是如何組織數據、查詢數據的,我們總結一下:
1、InnoDB存儲引擎的最小存儲單元是頁,頁可以用於存放數據也可以用於存放鍵值+指針,在B+樹中葉子節點存放數據,非葉子節點存放鍵值+指針。
2、索引組織表通過非葉子節點的二分查找法以及指針確定數據在哪個頁中,進而在去數據頁中查找到需要的數據;
那麼回到我們開始的問題,通常一棵B+樹可以存放多少行數據?
這裡我們先假設B+樹高為2,即存在一個根節點和若幹個葉子節點,那麼這棵B+樹的存放總記錄數為:根節點指針數*單個葉子節點記錄行數。
上文我們已經說明單個葉子節點(頁)中的記錄數=16K/1K=16。(這裡假設一行記錄的數據大小為1k,實際上現在很多互聯網業務數據記錄大小通常就是1K左右)。
那麼現在我們需要計算出非葉子節點能存放多少指針,其實這也很好算,我們假設主鍵ID為bigint類型,長度為8位元組,而指針大小在InnoDB源碼中設置為6位元組,這樣一共14位元組,我們一個頁中能存放多少這樣的單元,其實就代表有多少指針,即16384/14=1170。那麼可以算出一棵高度為2的B+樹,能存放1170*16=18720條這樣的數據記錄。
根據同樣的原理我們可以算出一個高度為3的B+樹可以存放:1170117016=21902400條這樣的記錄。所以在InnoDB中B+樹高度一般為1-3層,它就能滿足千萬級的數據存儲。在查找數據時一次頁的查找代表一次IO,所以通過主鍵索引查詢通常只需要1-3次IO操作即可查找到數據。
2. 怎麼得到B+樹的高度?
上面我們通過推斷得出B+樹的高度通常是1-3,下麵我們從另外一個側面證明這個結論。在InnoDB的表空間文件中,約定page number為3的代表主鍵索引的根頁,而在根頁偏移量為64的地方存放了該B+樹的page level。如果page level為1,樹高為2,page level為2,則樹高為3。即B+樹的高度=page level+1;下麵我們將從實際環境中嘗試找到這個page level。
在實際操作之前,你可以通過InnoDB元數據表確認主鍵索引根頁的page number為3,你也可以從《InnoDB存儲引擎》這本書中得到確認。
SELECT
b.name, a.name, index_id, type, a.space, a.PAGE_NO
FROM
information_schema.INNODB_SYS_INDEXES a,
information_schema.INNODB_SYS_TABLES b
WHERE
a.table_id = b.table_id AND a.space <> 0;執行結果:

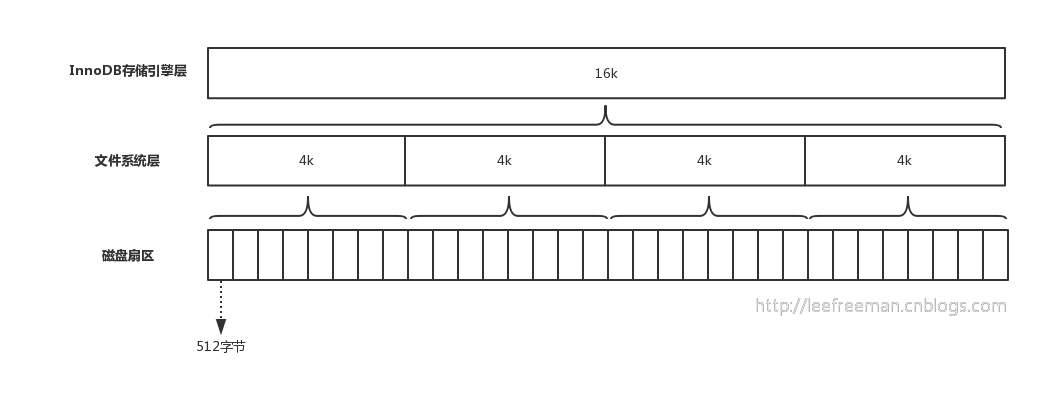
可以看出資料庫dbt3下的customer表、lineitem表主鍵索引根頁的page number均為3,而其他的二級索引page number為4。關於二級索引與主鍵索引的區別請參考MySQL相關書籍,本文不在此介紹。
下麵我們對資料庫表空間文件做相關的解析:
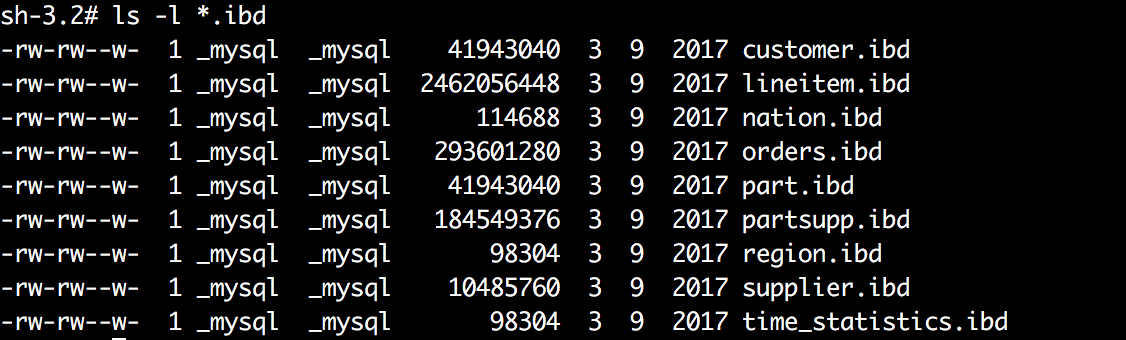
因為主鍵索引B+樹的根頁在整個表空間文件中的第3個頁開始,所以可以算出它在文件中的偏移量:16384*3=49152(16384為頁大小)。
另外根據《InnoDB存儲引擎》中描述在根頁的64偏移量位置前2個位元組,保存了page level的值,因此我們想要的page level的值在整個文件中的偏移量為:16384*3+64=49152+64=49216,前2個位元組中。
接下來我們用hexdump工具,查看表空間文件指定偏移量上的數據:

linetem表的page level為2,B+樹高度為page level+1=3;
region表的page level為0,B+樹高度為page level+1=1;
customer表的page level為2,B+樹高度為page level+1=3;
這三張表的數據量如下:

總結:
lineitem表的數據行數為600多萬,B+樹高度為3,customer表數據行數只有15萬,B+樹高度也為3。可以看出儘管數據量差異較大,這兩個表樹的高度都是3,換句話說這兩個表通過索引查詢效率並沒有太大差異,因為都只需要做3次IO。那麼如果有一張表行數是一千萬,那麼他的B+樹高度依舊是3,查詢效率仍然不會相差太大。
region表只有5行數據,當然他的B+樹高度為1。
3. 小結
本文從一個問題出發,逐步介紹了InnoDB索引組織表的原理、查詢方式,並結合已有知識,回答該問題,結合實踐來證明。當然為了表述簡單易懂,文中忽略了一些細枝末節,比如一個頁中不可能所有空間都用於存放數據,它還會存放一些少量的其他欄位比如page level,index number等等,另外還有頁的填充因數也導致一個頁不可能全部用於保存數據。關於二級索引數據存取方式可以參考MySQL相關書籍,他的要點是結合主鍵索引進行回表查詢。
來源:cnblogs.com/leefreeman/p/8315844.html
整編:二師兄
關註微信公眾號【悟能之能】瞭解更多編程技巧。