題面: 為了在即將到來的晚會上有更好的演出效果,作為AAA合唱隊負責人的小A需要將合唱隊的人根據他們的身高排出一個隊形。假定合唱隊一共N個人,第i個人的身高為Hi米(1000<=Hi<=2000),並已知任何兩個人的身高都不同。假定最終排出的隊形是A 個人站成一排,為了簡化問題,小A想出瞭如下排隊的 ...
題面:
為了在即將到來的晚會上有更好的演出效果,作為AAA合唱隊負責人的小A需要將合唱隊的人根據他們的身高排出一個隊形。假定合唱隊一共N個人,第i個人的身高為Hi米(1000<=Hi<=2000),並已知任何兩個人的身高都不同。假定最終排出的隊形是A 個人站成一排,為了簡化問題,小A想出瞭如下排隊的方式:他讓所有的人先按任意順序站成一個初始隊形,然後從左到右按以下原則依次將每個人插入最終棑排出的隊形中:
-第一個人直接插入空的當前隊形中。
-對從第二個人開始的每個人,如果他比前面那個人高(H較大),那麼將他插入當前隊形的最右邊。如果他比前面那個人矮(H較小),那麼將他插入當前隊形的最左邊。
當N個人全部插入當前隊形後便獲得最終排出的隊形。
例如,有6個人站成一個初始隊形,身高依次為1850、1900、1700、1650、1800和1750,
那麼小A會按以下步驟獲得最終排出的隊形:
1850
-
1850 , 1900 因為 1900 > 1850
-
1700, 1850, 1900 因為 1700 < 1900
-
1650 . 1700, 1850, 1900 因為 1650 < 1700
-
1650 , 1700, 1850, 1900, 1800 因為 1800 > 1650
-
1750, 1650, 1700,1850, 1900, 1800 因為 1750 < 1800
因此,最終排出的隊形是 1750,1650,1700,1850, 1900,1800
小A心中有一個理想隊形,他想知道多少種初始隊形可以獲得理想的隊形
大概思路:從最後的結果來看,隊尾或隊頭一定是最後入隊的,所以每次都分離隊頭和隊尾,分別討論他們的狀態求解。(動規)
這個思路有點抽象。。舉個例子解釋一下 (以輸入 1 2 3 5 4 作為例子)
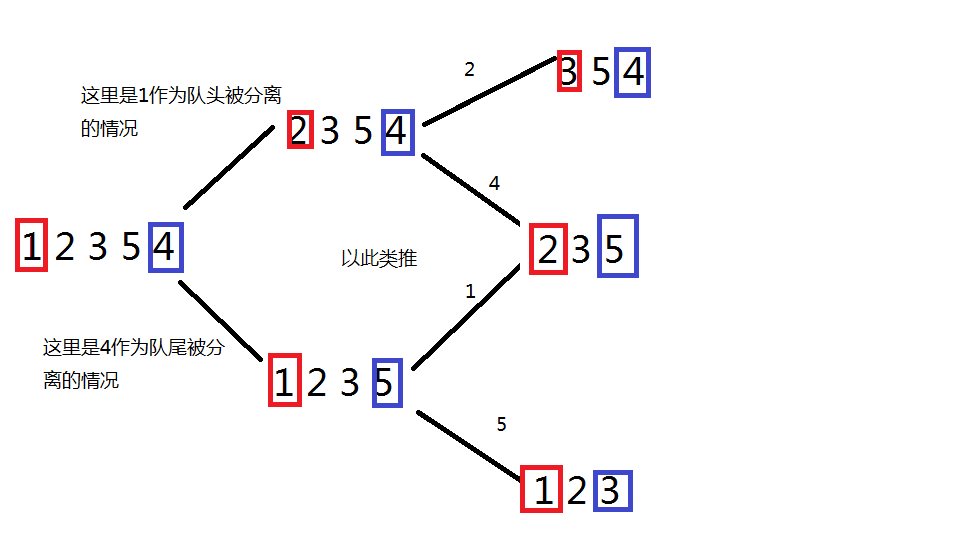
真的就是這麼簡單的分下去嗎?
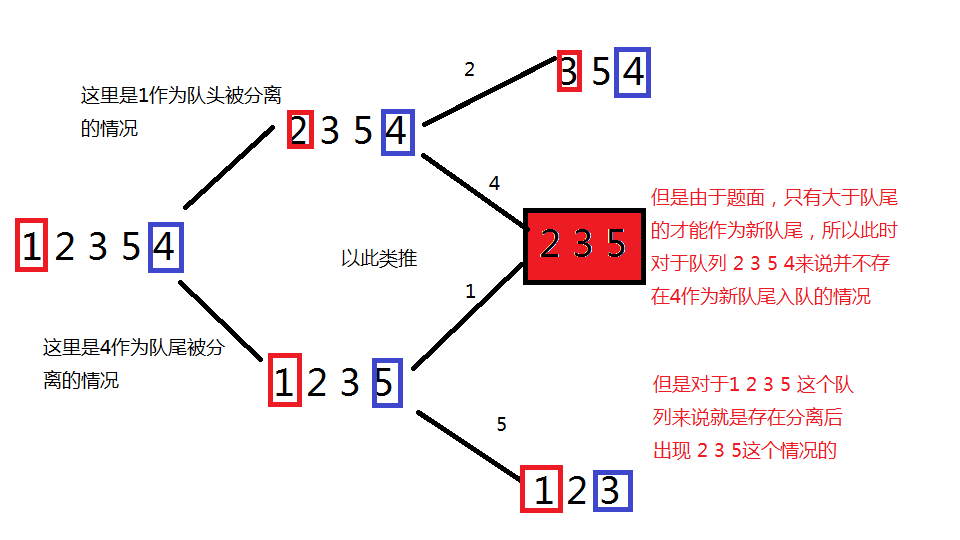
這個問題怎麼解決呢?
這時,我們假設當前要討論的數為x,刪去x的隊列隊頭值為L,隊尾值為R。就能發現

x作為新隊尾時也是同理(這裡就不寫了)
所以可以根據上圖推出動態轉移方程式
我們設隊列為q[],方案數存儲在dp[][][]中。
for(int len=n-1;len>=1;len--) { for(int l=1,r=len;r<=n;l++,r++) { dp[l][r][0]=((q[l]<q[r+1])*dp[l][r+1][1]+(q[l-1]<q[l])*dp[l-1][r][0])%Mod; dp[l][r][1]=((q[r]>q[l-1])*dp[l-1][r][0]+(q[r]<q[r+1])*dp[l][r+1][1])%Mod; } }
這裡的0代表作為隊頭入隊,1代表作為隊尾入隊。
最重要的部分到這裡就結束啦!
下麵是代碼
#include<iostream> #include<cstdio> using namespace std; int dp[1010][1010][2]; int q[1010]; int Mod=19650827; int n; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&q[i]); } q[0]=Mod; q[n+1]=-Mod; dp[1][n][0]=dp[1][n][1]=1; for(int len=n-1;len>=1;len--) { for(int l=1,r=len;r<=n;l++,r++) { dp[l][r][0]=((q[l]<q[r+1])*dp[l][r+1][1]+(q[l-1]<q[l])*dp[l-1][r][0])%Mod; dp[l][r][1]=((q[r]>q[l-1])*dp[l-1][r][0]+(q[r]<q[r+1])*dp[l][r+1][1])%Mod; } } int ans=0; for(int i=1;i<=n;i++) { ans=(ans+dp[i][i][0])%Mod;//這裡直接輸出dp[1][n][0]+dp[1][n][1]也行 } printf("%d",ans); return 0; }
蒟蒻的第一篇博客!(放個禮花吧先)


