樹的結構說得差不多了,現在我們來說說一種數據結構叫做哈希表(hash table),哈希表有是乾什麼用的呢?我們知道樹的操作的時間複雜度通常為O(logN),那有沒有更快的數據結構?當然有,那就是哈希表; 1.哈希表簡介 哈希表(hash table)是一種數據結構,提供很快速的插入和查找操作(有的 ...
樹的結構說得差不多了,現在我們來說說一種數據結構叫做哈希表(hash table),哈希表有是乾什麼用的呢?我們知道樹的操作的時間複雜度通常為O(logN),那有沒有更快的數據結構?當然有,那就是哈希表;
1.哈希表簡介
哈希表(hash table)是一種數據結構,提供很快速的插入和查找操作(有的時候甚至刪除操作也是),時間複雜度為O(1),對比時間複雜度就可以知道哈希表比樹的效率快得多,並且哈希表的實現也相對容易,然而沒有任何一種數據結構是完美的,哈希表也是;哈希表最大的缺陷就是基於數組,因為數組初始化的時候大小是確定的,數組創建後擴展起來比較困難;
當哈希表裝滿了之後,就要把數據轉移到一個更大的哈希表中,這會很費時間,而且哈希表不支持有順序的遍歷,因為從哈希表中遍曆數據是隨機的;所以我們使用哈希表的前提是:不需要有序的遍曆數據,可以大概知道數據量的多少;滿足這兩點就可以用哈希表;
那有人就要問了,說得這麼厲害,哈希表到底是什麼樣子的啊?下麵就隨便說兩個吧。。。
很經典的例子就是英語字典,我們查字典的時候可以根據這個單詞就可以找到第xxx頁,在這裡該單詞和頁數就對應起來了,這可以說是一個哈希表;
再舉個現實中的例子,在上學的時候每個人在學校里都會有一個學號,你這個人在學校中就對應這個學號,假如校長手上有一個記錄全校學生的表,然後根據學號找一個學生時,就能很快鎖定這個學生的姓名,性別,班級等信息;有沒有想過假如沒有學號的話,校長想找一個學生就只能根據姓名去找,可是同名同姓的人這麼多,想找到目標學生不是一件容易的事。。。。。
ok,在這裡哈希表可以看作是校長手上的那個表(其實就是一個數組),我們根據我們要存的信息生成一個表中的位置的號碼(在這裡這個號碼就是數組的下標),根據這個號碼我們就知道該數據存在數組的哪個位置,然後將數據保存進去就可以了;假如有個大小為20的數組,我要存“aaa”,我們可以想個很厲害的辦法將這個字元串變成一個比較小的數字,比如是10,那麼就把這個字元串存到數組的第10個位置,這樣做的好處就是下次如果要從哈希表中查詢(或刪除)“aaa”這個字元串時,只需要將“aaa”字元串算出那個號碼10,然後直接去數組中第10個位置找一個看有沒有這個字元串,是不是很簡單啊!
所以現在我們需要解決的就是想個很厲害的辦法可以將字元串變成一個比較小的數字(這個過程叫做哈希化),還要保證這個數字不能超過數組的最大邊界!
2 哈希化
哈希化就是想辦法將我們要保存的數據對應一個數組下標,在數組的該位置下保存數據;我們可以把這個過程專業一點的說一下:把要保存的數據,通過哈希函數轉化為對應的數組下標;現在我們的目標就是怎麼編寫一個哈希函數可以使得字元串變成數組下標;
這裡我們可以假設一個字元串t數組的大小為30,String[] str = new String[30]; 要存“cats”這個單詞,最容易想到的辦法就是用ASCII碼,但是由於ASCII碼太多了不好記,於是我們可以自己設置一套規則,我就假設a到z分別對應1到26,外加空格對應0,現在一套最簡陋的規則就出來了,我那麼“cats”這個單詞:c = 3,a = 1,t = 20,s = 19,現在“cats”有兩種辦法變成數組的下標;
額外補充一下:假如我們要保存的字元串有50個,那麼我們new的數組大小一定要是它的兩倍大,即 new String[100];,後面會說到這個原因
2.1哈希函數實現一
怎麼實現比較好呢?別想那麼多,直接相加就好,3+1+20+19 = 43,這個時候就有個小問題,我們的數組的大小為30,也就是說數組下標最大值是29,而這裡我們的數字為43,怎麼將43變成29以內的數(包括29)呢?因為任何數除以30的餘數只都在0-29之間,於是我們用43除以30拿到餘數13,那麼我們就把”cats“放到數組下標為13的位置,str[13] = "cats";
這種哈希函數的實現很容易,但是往往越容易的東西缺點就越大,最大的缺陷就是有很多單詞變成數字是相同的,比如was,tin,give等100多個單詞變成數字後都是43,然後我們恰巧添加單詞的時候就是這些單詞,現在問題來了,多個單詞最後算出來的數組下標很大概率上是一樣的,也就是數組一個位置要放多個數據,怎麼解決這個問題呢?我們可以換一種哈希函數的實現來降低這個概率
2.2 哈希函數實現二
由2.1可以知道太多的單詞變成數字的結果是一樣的,那麼我們就要想辦法為每一個單詞都對應一個獨一無二的整數,然後用這個整數除以數組的大小取餘數,就可以知道該單詞在數組中的存放位置;
於是啊,我們可以利用冪的連乘來得到這個獨一無二的整數,比如“cats”用這種計算方法:3*273+1*272+20*271+19*270,有點類似二進位變成十進位,通過這個演算法,可以得到一個獨一無二的整數,其他的任何單詞通過這種方法算出來的結果幾乎是不可能相等的,有興趣的可以試試;然後將這個計算結果除以30取餘數,就可以得到一個數組的位置,然後將該字元串丟到裡面即可;

不知道大家有沒有發現這種方法的一個問題,因為數組的大小是一定的,而且我們是通過取餘數來得到數組的位置,那麼問題來了,即使是兩個不相同的整數分別除以30,最後的餘數是相等的;
就比如有兩個字元串通過冪的連乘最後得到32和62(當然我們這裡肯定不會得到這兩個整數,為了好理解隨便拿兩個數),雖然這兩個數是獨一無二的,但是除以30餘數都為2,那麼兩個數據要保存到哈希表中肯定會有衝突,下後面我們來解決一下這個衝突;
有個簡單的哈希函數實現看一下(雖然還可以進行修改一下,但是這個已經差不多了);


3.衝突
衝突的原因就是兩個獨一無二的整數除以數組的大小,取餘數是相等的,而數組中一個位置只能存一個數據,這就導致了衝突,解決衝突的辦法有兩種;
3.1 解決方法一(開放地址法)
還記得前面說過數組的大小要為實際數量的兩倍嗎?就是為了這個時候用的,假如一個單詞已經放在了數組的第15個位置那裡,另外一個單詞本來也要放在第15的位置,由於這個位置已經被別人占了。那就放在數組的另外一個位置上,反正還有很多數組比較大,這種方式叫做------開放地址法
3.2 解決方法二(鏈地址法 )
既然有兩個數據都要放在數組的一個位置上,那就想辦法把第二個數據連在第一個數據後面,通過第一個數據可以找到第二個數據,而數組中只保存第一個數據的地址;其實就是一句話,數組中每個位置放一個鏈表;
這種方法的好處很明顯,完美解決上述衝突,不需要用什麼花里胡哨的操作;缺陷就是當鏈表太長了,我們要查詢這個鏈表的最後面的數據,只能慢慢遍歷這個鏈表,而我們知道,鏈表的優勢是插入和刪除,而對於查詢這種操作是比較坑爹的,而我們前面用了紅黑樹這樣的結構來完美解決鏈表的缺點;最後,我們就差不多想到了一個比較實用的方法:數組的每個位置都存放一個鏈表,當鏈表的節點很少的時候,那就用鏈表吧!但是當鏈表慢慢的變長,當節點數目到達一個界限的時候,我們就把這個鏈表變成一個紅黑樹,比較完美的方案,這也叫做------鏈地址法
順便一提,jdk7的HashMap就是數組中放鏈表,即使鏈表很長也不會變紅黑樹;jdk8中的HashMap才增加了變紅黑樹這個操作
4.開放地址法
所謂的開放地址法就是:根據我們要保存的數據計算出來的數組下標的那個位置已經存放了數據,這個時候我們就要再找一個空位置,然後將要保存的數據丟進去即可,那麼怎麼找比較好呢?這裡提供三種方式,線性探測,二次探測和再哈希法,下麵就看看這三種方式到底是怎麼工作的;
4.1 線程探測
看名字線性就知道是從前往後尋找空的位置,舉個很簡單的例子,當一個字元串經過運算對應於數組下標為52,然而此時52這個位置上已經有了數據,那麼就嘗試放到53的位置,假如53的位置也已經放了數據,那就放到54位置,就這樣一直往後慢慢找,直到找到一個空的位置就把數據放進去;而此時找的次數越多,假如已經找到56的位置,那麼從53到56這麼多位置叫做填充序列,當填充序列很長的時候,我們就稱為原始聚集,下圖所示:

這裡填充序列的中有5個填充單元,我們也可以說步數為1,每次探測都是前進一步;我們可以知道當探測的次數越多的時候,說明聚集越嚴重,下一次再想添加到這個位置的數據的效率就越低;
還有就是當哈希表填充得越滿,效率也就越低,所以當哈希表快滿了之後就要擴展,而java中數組是不能直接進行擴展的,需要再新建一個數組,然後想辦法將這個哈希表中的數據複製到新的數組中,註意,這裡不能直接複製,因為新的數組的容量和原來的數組不一樣,那麼原來哈希表中所有的數據必須要重新哈希化,然後放入到新的數組中,非常耗時....
4.2 二次探測
根據前面我們的線性探測可以知道,假如經過哈希函數計算出來的原始數組下標為x,那麼線性探測的位置是x+1,x+2,x+3,x+4.....,;那麼 進行二次探測找的位置就是x+12,x+22,x+32,x+42.....其實就是按照步數的平方進行探測看裡面有沒有數據,沒有的話才放進去新的數據,二次探測可以防止聚集太長所導致的效率下降問題;
對於二次探測來說,如果當前計算出來的位置為x,首先會探測x後面一個位置,如果這個位置有數據,那就多往後4個位置看有沒有數據,假如還是有數據,那麼二次探測可能會覺得你這個聚集特別長,於是這次跳得更遠的位置,當前位置後面的16的位置等等,直到最後跳過整個數組, 這樣可以避免一個一個的位置慢慢探測的底下效率,二次探測下圖所示:
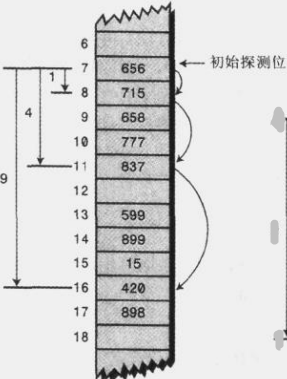
二次探測也有點問題,會導致二次聚集,那什麼又是二次聚集呢?其實跟原始聚集差不多吧!比如184,302,420,544這幾個整數都要放到哈希表中,而且這幾個數經過哈希演算法算出來的數組下標都為7,302需要以1步長進行探測,而420要先以1為步長,然後以4步長進行探測,而544要先以1為步長,然後以4為步長,最後以16步長進行探測,假如後面還有數據對應的數組下標為7,那麼還是要重覆這個步驟,而且是越來越長....這也是一種聚集,個人感覺從某種意義來說和原始聚集性質差不多吧!
二次探測不常用,因為有更好的辦法解決,就是再哈希法;
4.3 再哈希法
用再哈希法可以消除原始聚集和二次聚集,那麼什麼是再哈希法呢?我們可以知道產生原始聚集和二次聚集的原因其實差不多,都是由於多個數據添加到哈希表中的同一個位置,然後根據步長一個一個位置的探測,直到找到一個空的位置,如果需要找的位置特別多,那麼這就是聚集,添加的效率的就會大幅度降低;
那麼我們就要想一種方法即使多個數據要放在哈希表的同一個位置,但是不需要從頭開始一個一個位置的探測,如果每個數據都可以產生一個獨一無二的步長那不就好了麽!然後直接根據這個步長探測該位置將數據丟進去就ok了;
於是我們準備了兩個哈希函數,一個哈希函數就是我們上面說到的可以產生對應的數組下標,另外一個哈希函數可以產生步長,其實就是多個數據放在同一個位置產發生衝突,就用這個哈希函數再次哈希化產生一個步長,根據這個步長進行探測就可以了,而不用每次都從第一個步長開始;比如下麵就有一個產生步長的哈希函數,我們可以知道步長的範圍是1-constant,註意步長不能為0,否則就原地踏步了。。。

上圖中,假如我們往哈希表中添加的數據是數字,那就直接將數據和數組大小取餘得到數組下標,這裡的key就是我們的數據,constant只要是小於數組容量的一個質數,隨便什麼都可以
順便一提:再哈希法使用的前提必須保證數組的容量為一個質數,因為這樣才能使得所有位置都被探測到;可以試試假如數組容量為15,步長為5,一個數據經過計算得到額數組下標為0,那麼探測的位置應該為:(0+5)%15 = 5,、(5+5)%15 = 10,(10+5)%15 = 0,只會探測0、5、10這三個位置;但是如果數組容量為質數13,步長為5,第一個數據下標還是0,那麼探測位置為:(0+5)%13 = 5,、(5+5)%13 = 10,(10+5)%13 = 2、(2+5)%13 = 7,(7+5)%13 = 12,(12+5)%13 = 4,(4+5)%13 = 9等等,可以看到每次探測的位置都不一樣,可以探測到數組中所有位置只要有空的就把數據當進去即可;
假如使用的是開放地址法,那麼探測序列就用這個再哈希法生成,其實很容易!
5.鏈地址法
可以看到上面的開放地址法有點麻煩,需要找到探測序列真的是日了狗了,麻煩的我都不想看了,如果可以不用這麼麻煩那該多好呀,ok,那就用鏈地址法吧!就類似下麵這樣的結構,原始的數組中不直接保存數據,每個位置只是保存第一個數據的引用,通過該位置第一個引用就可以取到後面所有的數據!如果鏈表太長遍歷起來就比較費勁,可以轉為紅黑樹效率就高了很多;
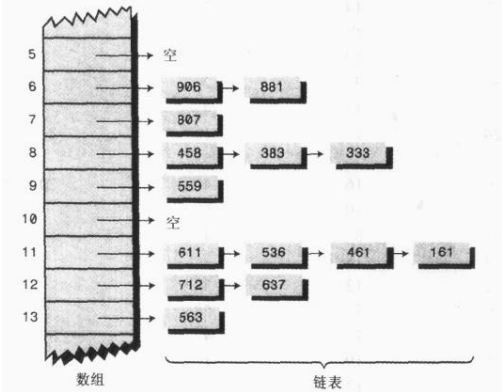
這裡其實沒什麼好說的,因為數組和鏈表的使用很熟悉了,沒什麼特別難的東西,基本邏輯:只需要新建一個MyHashTable的類,這個類中有幾個屬性:一個數組,一個int類型的屬性標識數組真實容量的大小;最好有個節點類為靜態內部類,這個靜態內部類中實現了對鏈表的增刪改查的操作;然後在MyHashTable類中寫一個哈希函數的方法,根據這個哈希函數得出來的數組下標,最後對數組的增刪改查了!
6.總結
哈希表其實還可以用在外部存儲中,也就是硬碟中,有興趣的可以看看,不過我感覺到這裡就差不多了!其實哈希表的內容沒多少吧,最主要的就是哈希函數的選取,選擇一個好的哈希函數可以使得我們的哈希表的效率更高!然後就是數組中存數據的方式,可以直接在數組中存數據,也可以在數組中存節點的引用,其實吧,知不知道二維數組?在我們這個數組中每個位置存的是另外一個數組的引用,這樣其實也行,由於擴展起來很困難,使用鏈表比使用二維數組好。。。



