題目鏈接 Description A power network consists of nodes (power stations, consumers and dispatchers) connected by power transport lines. A node u may be sup ...
Description
A power network consists of nodes (power stations, consumers and dispatchers) connected by power transport lines. A node u may be supplied with an amount s(u) >= 0 of power, may produce an amount 0 <= p(u) <= pmax(u) of power, may consume an amount 0 <= c(u) <= min(s(u),cmax(u)) of power, and may deliver an amount d(u)=s(u)+p(u)-c(u) of power. The following restrictions apply: c(u)=0 for any power station, p(u)=0 for any consumer, and p(u)=c(u)=0 for any dispatcher. There is at most one power transport line (u,v) from a node u to a node v in the net; it transports an amount 0 <= l(u,v) <= lmax(u,v) of power delivered by u to v. Let Con=Σuc(u) be the power consumed in the net. The problem is to compute the maximum value of Con.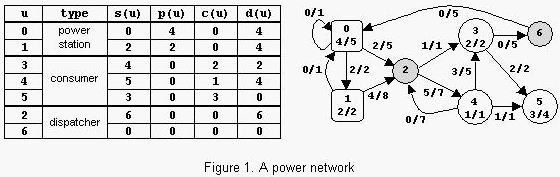
An example is in figure 1. The label x/y of power station u shows that p(u)=x and pmax(u)=y. The label x/y of consumer u shows that c(u)=x and cmax(u)=y. The label x/y of power transport line (u,v) shows that l(u,v)=x and lmax(u,v)=y. The power consumed is Con=6. Notice that there are other possible states of the network but the value of Con cannot exceed 6.
Input
There are several data sets in the input. Each data set encodes a power network. It starts with four integers: 0 <= n <= 100 (nodes), 0 <= np <= n (power stations), 0 <= nc <= n (consumers), and 0 <= m <= n^2 (power transport lines). Follow m data triplets (u,v)z, where u and v are node identifiers (starting from 0) and 0 <= z <= 1000 is the value of lmax(u,v). Follow np doublets (u)z, where u is the identifier of a power station and 0 <= z <= 10000 is the value of pmax(u). The data set ends with nc doublets (u)z, where u is the identifier of a consumer and 0 <= z <= 10000 is the value of cmax(u). All input numbers are integers. Except the (u,v)z triplets and the (u)z doublets, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.Output
For each data set from the input, the program prints on the standard output the maximum amount of power that can be consumed in the corresponding network. Each result has an integral value and is printed from the beginning of a separate line.Sample Input
2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)20
7 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 (2,4)7
(3,5)2 (3,6)5 (4,2)7 (4,3)5 (4,5)1 (6,0)5
(0)5 (1)2 (3)2 (4)1 (5)4
Sample Output
15 6題意：由n個點構成的圖，其中np個點為發電站最大發電量為zi，nc個點為用戶最大消耗電量為zj，剩餘點為中轉點不產電也不消耗電，求此電網最大消耗電量？ 思路：可將np個發電站看做源點，nc個用戶點看做匯點，為了構成單源單匯點，增加一個源點0連向np個發電站，其邊權為發電站的最大發電量；增加一個匯點n+1，由所有的用戶連向匯點n+1，其邊權為用戶的最大消耗電量。此時，就變成了單純的最大流問題。 註：第一次寫Dinic最大流代碼，簡單介紹一下Dinic演算法： EK（EdmondsKarp）最大流的思想為，每次採用bfs搜索找到一條增廣路（設流量為flow），改變這條路徑上的所有的邊權值都減少flow，同時這條路徑上的所有反向邊權值增加flow，重覆直至找不到增廣路為止。 Dinic演算法很明顯是EK的一個優化演算法，其先採用 bfs 將圖按深度分層，然後 dfs 找到所有的增廣路並同樣改變所有的邊權值以及反向邊的權值，很明顯這樣dfs貪心的找到所有的增廣路並不是最優解，故迴圈再用bfs重新分層，dfs找增廣路，直到bfs分層沒有路徑能走到匯點，此時即是最大流量了。 最大流Dinic代碼如下：
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <cstdlib> #include <queue> using namespace std; const int N = 105; const int MAXN = 1e9 + 7; struct Edge { int to; int value; int next; }e[2*N*N]; int head[N], cnt; int deep[N]; int n, np, nc, m; void insert(int u, int v, int value) { e[++cnt].to = v; e[cnt].value = value; e[cnt].next = head[u]; head[u] = cnt; } void init() { memset(head, -1, sizeof(head)); cnt = -1; } bool BFS() { memset(deep,-1,sizeof(deep)); queue<int> Q; deep[0] = 0; Q.push(0); while (!Q.empty()) { int u = Q.front(); Q.pop(); for (int edge = head[u]; edge != -1; edge = e[edge].next) { int v = e[edge].to; if (deep[v] == -1 && e[edge].value > 0) { deep[v] = deep[u] + 1; Q.push(v); } } } if (deep[n + 1] == -1) return false; return true; } int DFS(int u,int flow_pre) { if (u == n + 1) return flow_pre; int flow = 0; for (int edge = head[u]; edge != -1; edge = e[edge].next) { int v = e[edge].to; if (deep[v] != deep[u]+1 || e[edge].value==0) continue; int _flow= DFS(v, min(flow_pre, e[edge].value)); flow_pre -= _flow; flow += _flow; e[edge].value -= _flow; e[edge ^ 1].value += _flow; if (flow_pre == 0) break; } if (flow == 0) deep[u] = -1; return flow; } int GetMaxFlow() { int ans = 0; while (BFS()) { ans += DFS(0,MAXN); } return ans; } int main() { while (scanf("%d%d%d%d", &n, &np, &nc, &m) != EOF) { init(); int u, v, z; for (int i = 0; i < m; i++) { scanf(" (%d,%d)%d", &u, &v, &z); insert(u+1, v+1, z); insert(v+1, u+1, 0); } for (int i = 0; i < np; i++) { scanf(" (%d)%d", &u, &z); insert(0, u+1, z); insert(u+1, 0, 0); } for (int i = 0; i < nc; i++) { scanf(" (%d)%d", &u, &z); insert(u + 1, n + 1, z); insert(n + 1, u + 1, 0); } printf("%d\n",GetMaxFlow()); } }
