這一篇我們來看看紅黑樹,首先說一下我啃紅黑樹的一點想法,剛開始的時候比較蒙,what?這到底是什麼鬼啊?還有這種操作?有好久的時間我都緩不過來,直到我玩了兩把王者之後回頭一看,好像有點兒意思,所以有的時候碰到一個問題困擾了很久可以先讓自己的頭腦放鬆一下,哈哈! 不瞎扯咳,開始今天的正題; 前提:看紅 ...
這一篇我們來看看紅黑樹,首先說一下我啃紅黑樹的一點想法,剛開始的時候比較蒙,what?這到底是什麼鬼啊?還有這種操作?有好久的時間我都緩不過來,直到我玩了兩把王者之後回頭一看,好像有點兒意思,所以有的時候碰到一個問題困擾了很久可以先讓自己的頭腦放鬆一下,哈哈!
不瞎扯咳,開始今天的正題;
前提:看紅黑樹之前一定要先會搜索二叉樹
1.紅黑樹的概念
紅黑樹到底是個什麼鬼呢?我最開始也在想這個問題,你說前面的搜索二叉樹多牛,各種操作效率也不錯,用起來很爽啊,為什麼突然又冒出來了紅黑樹啊?
確實,搜索二叉樹一般情況下足夠了,但是有個很大的缺陷,向搜索二叉樹中插入的數據必須是隨機性比較強大的;如果你是插入的順序是按照一定的順序的,比如10、9、8、7、6、5、4、3、2、1,你把這十個數據插入到搜索二叉樹中你就會看到一個比較有趣的現象;瑪德,這二叉樹居然變成鏈表了(此時的鏈表也可以說是不平衡樹),這就意味著變成鏈表之後就喪失了身為搜索二叉樹的所有特性,這就很可怕,而且當這種有順序的數據很多的時候,就特別坑爹,查詢的效率賊慢;
所以就出現了紅黑樹這種數據結構,可以說這是一種特殊的搜索二叉樹,是對搜索二叉樹進行改進之後的一種很完美的二叉樹,這種數據結構最厲害的就是可以自動調整樹的結構,就比如上面這種有順序的數據插入到紅黑樹之後,紅黑樹就會自動的啪啪啪給你一頓調節最後還是一棵正常的搜索二叉樹,不會變成鏈表就對了;
那麼就有人要問了,要怎麼樣才能將一個搜索二叉樹變成紅黑樹呢?
答:這很容易回答,字如其名,你把搜索二叉樹的每個節點要麼塗成紅色要麼塗成黑色,使得最後這個二叉樹中所有節點只有紅黑兩種顏色,這就是一個紅黑樹;
這時還有人要問了,是不是可以隨意把搜索二叉樹中的節點塗成紅色或者黑色呢?
答:emmmm.....你覺得有這麼容易麽?哪有這麼隨便的!肯定是要符合一些規則你才能塗啊,而且大佬們已經把這些規則總結出來了,我們只需要記好這些筆記就好了!
下麵我們就看看紅黑樹要滿足的規則:
(1):每個節點不是紅色就是黑色;
(2):根節點總是黑色;
(3):不能有兩個連續的紅色節點;
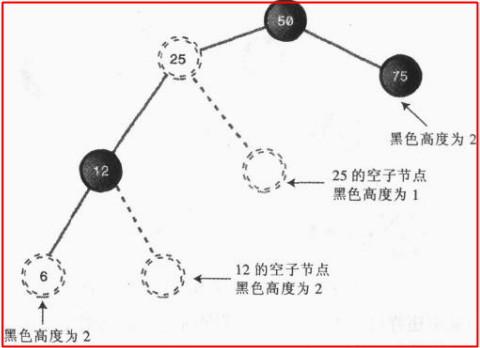
(4):從根節點到每一個葉節點或空子節點的黑色節點的數量一定要相同,這個黑色節點的數量叫做黑色高度,所以這個規則換句話來說就是根節點到每一個葉節點或空子節點的黑色高度相等;
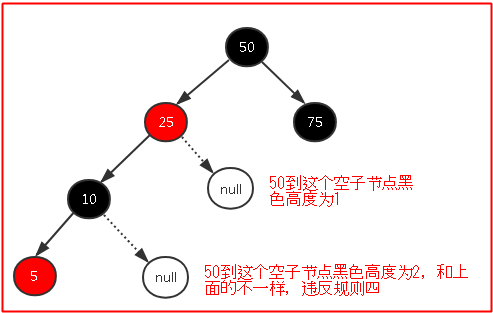
這四個規則很重要,任何紅黑樹都必須同時滿足這四個規則,否則就不是紅黑樹,前三個很容易,話說第四個的空子節點是什麼意思呢?字如其名,就是一個空的節點,裡面什麼都沒有,可以當作一個null節點,比如下圖所示,這個其實理解就好,不用在意;
第四條規則為了好理解才從根節點開始的,其實從任意一個節點開始也是一樣的;可以拆分為兩條,某個節點到該節點每一個葉節點的黑色高度要一樣,同時還要該節點到該節點的每一個空子節點的黑色高度要一樣;
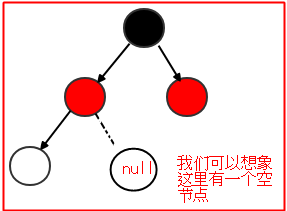
空子節點的定義為:非葉節點可以接子節點的位置;(註意,有的版本沒有這個空子節點這個說法,只是說每一個葉節點(NIL)都是黑色的。。。。而且這裡的葉節點和之前我們理解的葉節點還不一樣,看看下圖,但本篇我們還是按照空子節點的這個說法,參考《java數據結構和演算法第二版》),理解了之後其實是一樣的

我們再看看下麵這個我截的圖,假如不看那兩個空子節點,看起來好像是符合紅黑樹規則的,但是我們還要判斷根節點到每個空子節點的黑色高度是不是一樣,結果不一樣,於是下圖其實違背了規則四;
這裡繼續說一點東西:
新插入的節點必須是紅色的,為什麼呢?你想啊,你往一個正常的紅黑樹中插入一個黑色節點,肯定就會百分之百違反第四規則,這就比較坑,每插入一個節點你都要想辦法去調整整個樹的顏色和結構,這很影響效率;但是假如你插入的節點是紅色的,而且這個紅色節點還剛好是插入在一個黑色的葉節點那裡,誒呀,舒服,什麼都不用動;當然還有可能插入到另一個紅色節點下麵,所以插入紅色節點違反規則的概率是百分之五十,用腳趾頭都能想到新插入的節點肯定要是紅色的啊!
2.紅黑樹調整的方式
對了,知不知道電腦中紅黑樹怎麼區分紅黑色節點啊?我們不可能真的去給電腦中的節點塗顏色吧。。。。其實我們只需要在節點類中添加一個Boolean color的屬性即可,color為true表示黑色,false為紅色;
我們在插入紅色的節點的時候有兩種可能:(1)剛好把這個紅色節點插入到一個黑色節點下麵,這個時候直接添加就好;(2)比較不幸,插入到一個紅色節點下麵,這個時候就違反規則3,連續兩個節點為紅色,這個時候我們要對紅黑樹的顏色和進行一定調整;
我們對不符合規則的紅黑樹進行調整操作主要是分為兩個步驟:改變顏色和旋轉
改變顏色就不多說了,看名字就知道,我們重點就看看旋轉到底是什麼鬼?通過改變一些節點的顏色使得滿足紅黑樹規則;
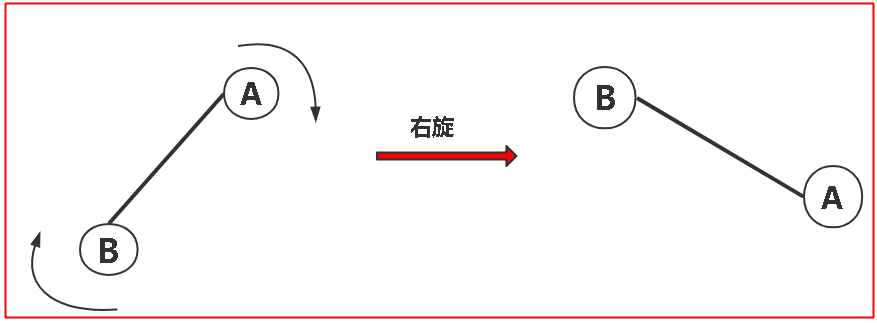
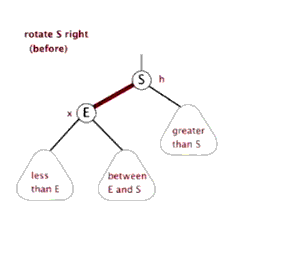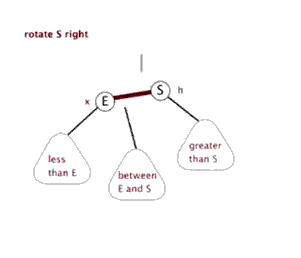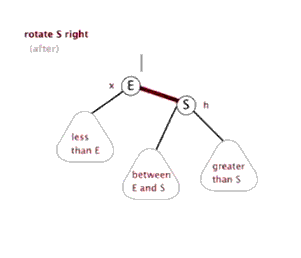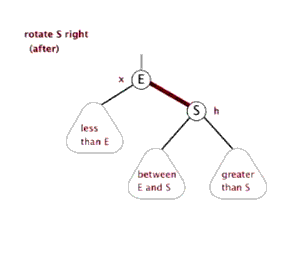
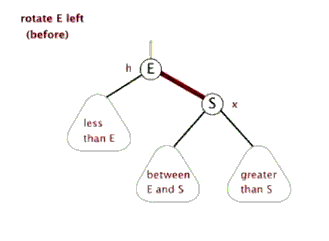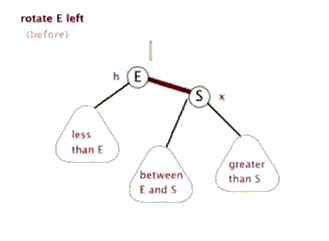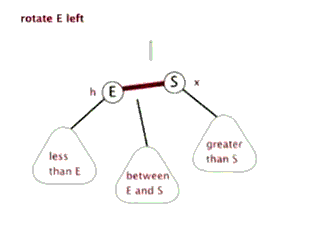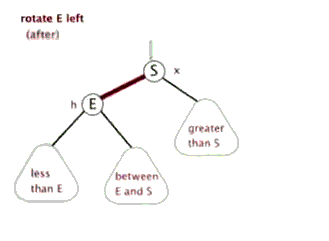
通常情況下旋轉分為左旋(逆時針)和右旋(順時針),我們就簡單看看右旋吧,左旋差不多;註意下圖這裡的右旋可不是繞著節點A旋轉啊,A叫做頂端,這裡相當於是把這兩個節點之間的路徑進行了一個旋轉;(這裡很像繞著A節點旋轉,很抱歉不是繞著A旋轉,下麵我們看看紅黑樹中的右旋就看的很明顯了。。。)
在紅黑樹中的右旋,在下圖中80是“頂端節點”,經過右旋之後頂端節點變為右子節點,而原來的左子節點50變為頂端節點,這樣調整了之後70這個節點就沒地方放了,於是我們可以順著右旋之後的50節點的右子節點找到可以存放的位置,也就是80的左子節點,我們可以把70這個節點的移動看作橫向移動;
從右往左看就是左旋,這裡就不詳說了。。。,
對了,順便提一下,假如這裡的70節點有子節點,那麼子節點也會跟著一起移動的;我們把70這個節點叫做80這個頂端節點的內側子孫節點,把30叫做頂端節點80的外側子孫節點,這個還是很好理解的,30這個節點在樹的靠外面,70這個節點始終都是在中裡面。。。。
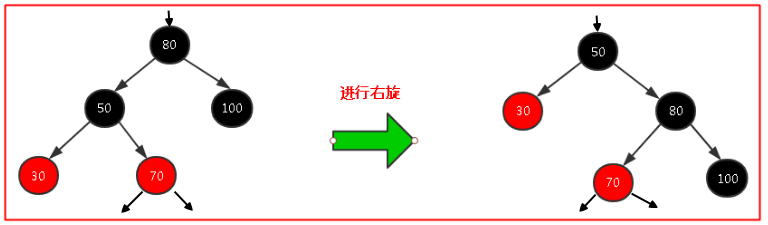
網上找到兩張動態的圖可以看看右旋和左旋,可以好好理解這旋轉,旋轉真的很重要!!!
3.添加紅黑樹節點
下麵我們通過慢慢的添加一個一個節點,看看紅黑樹當遇到問題的時候是怎麼調整的;
(1)

(2)
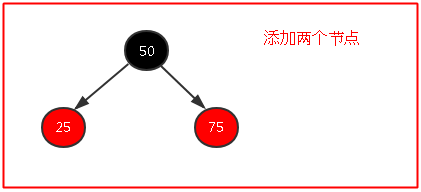
(3)右圖這種情況下根節點左邊兩層,右邊一層,稍微有點不平衡,但是沒有違反紅黑樹規則,於是我們不必在意什麼;但是假如一條路徑比另外一條路徑多兩層或者兩層以上,這個肯定是會違反紅黑樹規則的,為什麼呢?我也不是怎麼清楚可能是經過大佬們無數次試驗得出來的結論吧!

(4)
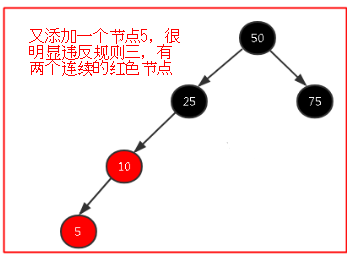
此時我們碰到這種情況,第一感覺是改變10和25的顏色,下圖所示,看起來貌似是符合紅黑樹結構的;但是我們要記住當一條路徑多於另外一條路徑兩層及以上的時候肯定會違反紅黑樹規則,我們再仔細看看這個圖就會發現違反了第四規則中:根節點到空子節點的黑色長度要一樣

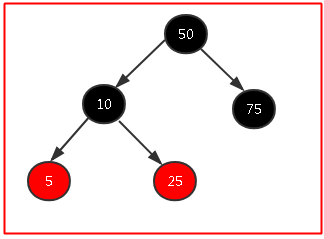
所以我們可以知道只是單純的改變顏色肯定是不能滿足紅黑樹規則的,我們還要再進行旋轉,我們以25為頂端節點進行右旋,變成了下圖,滿足條件,ok!
(5).對上面(4)中進行的完善
當我們以為(4)這就完美解決的時候,很抱歉還有另外一種情況,當我們新添加的紅色節點在10的右子節點上,下圖所示:
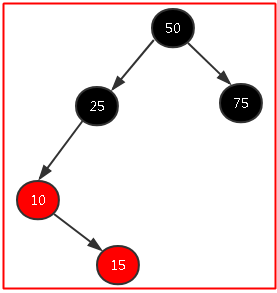
這種情況就比較坑爹,肯定不能像(4)中那樣右旋,比如我就不信這個邪,我就要右旋,於是結果如下圖一所示,我就默默地信了這個邪!
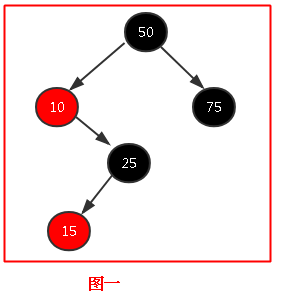
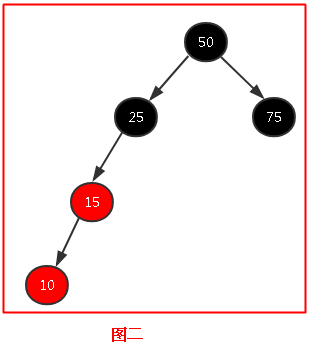
那麼我就要換一個方法了,我就想啊,如果我們能把這個圖變成(4)中的那樣的結構那不就可以直接用(4)中的解決方法了嗎?基於這個想法,我們可以先試著以10為頂點節點,和15節點一起進行左旋,如圖二所示,然後我們就發現世界原來一切如此美好,後面的就跟(4)中一樣了,這裡就不多說了;
但是在這裡要註意顏色的變換和上面那個有一點不同,(4)中是改變父節點和爺爺節點的顏色,而圖二是經過旋轉之後也是改變父節點和爺爺節點的顏色,就是相當於旋轉之前的當前節點和爺爺節點
現在我們把上面調整方式整理一下(想必大家應該知道爺爺節點的意思吧。。。通常都叫做祖父節點,我就喜歡叫爺爺節點,哈哈):
第一種:假如我們添加的紅色節點是添加在黑色節點下,完美;
第二種:假如我們添加的紅色節點不小心添加到紅色節點下,這裡要分為兩種情況:
假如是左節點(也可以叫做爺爺節點的外側子孫),那麼就改變父節點和爺爺節點的顏色,並且以爺爺節點為頂端節點進行右旋,就ok了;
假如是右節點(也可以叫做爺爺節點的內側子孫) ,那麼就改變當前節點和爺爺節點的顏色,然後要以父節點為頂端節點進行左旋,再繞爺爺節點右旋;
小知識:怎麼快速的判斷一個節點是不是它爺爺節點的外側子孫還是內側子孫呢?你要看當前節點和父節點是不是在同側,同側的就是外側節點,不同側就是內側節點;舉個例子,假如當前節點的父節點是左節點,當前節點也是屬於左節點,都是左邊,那當前節點就是其爺爺節點的外側節點,如果當前節點是右節點,那就是內側子孫。。。
(6).對上面(5)中進一步的完善
╮( ̄▽ ̄")╭,是不是覺得各種補充的內容啊,哈哈哈,正常!這是最後一個補充了。。。
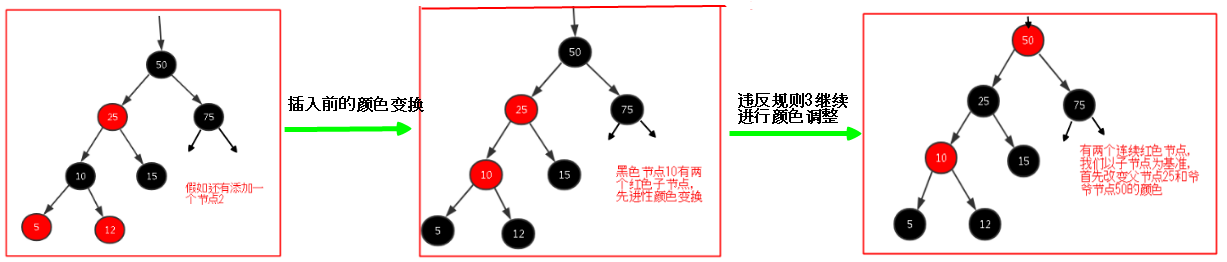
說出來你們可能不信,上面的(4)和(5)其實都是針對在節點插入之後導致樹不平衡而做出的調整,但是會有點小問題,就比如在(4)中,假如50這個節點不是根節點而是一個普通的紅色節點,那麼在我們首先進行顏色變換的時候就會出現問題,例如下圖,那麼我們後面的所謂右旋也就沒啥用了,所以我們要解決一下這種隱患,最好是在插入數據之前首先對紅黑樹中的這種有隱患的節點首先進行顏色調整或者旋轉;
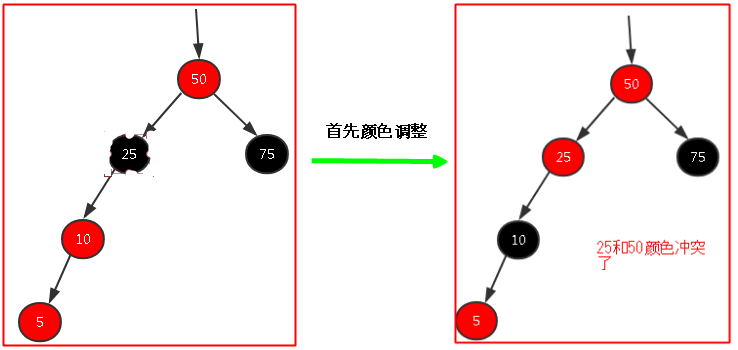
那麼肯定有人要問了,卧槽!這該怎麼做啊?我不會呀,怎麼辦?
答:不會才正常啊,才能顯示那些大佬很牛啊!我們只需要在插入節點之前對樹的一些有隱患的結構進行調整即可(顏色調整和旋轉),調整這個有隱患的結構是為了讓我們後續的插入節點更加方便;
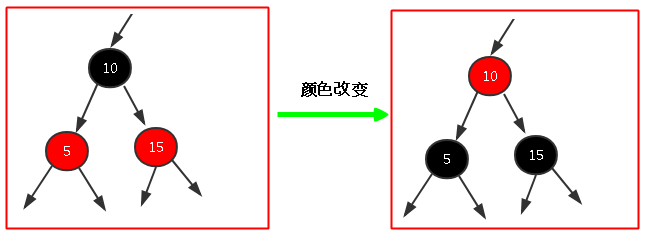
6.1.顏色調整:紅黑樹中我們要插入節點,其實是和搜索二叉樹一樣,從根節點開始一個一個的比較節點數值大小,小就繼續和左子節點比較.....最終肯定可以找到確定的位置,在這個找的過程中,假如一個節點為黑色,它的兩個子節點都為紅色,這就是一種有隱患的結構,我們需要將父節點和兩個子節點顏色都改變一下,下圖所示:
6.2.旋轉:在6.1中雖然對這樣的結構進行了顏色的改變,但是有個小缺陷,假如10節點的父節點是紅色的呢?那麼我們這樣改變顏色也是不符合紅黑樹規則三(不能有連續的兩個紅節點)的,於是我們還要進行旋轉操作,而旋轉操作的的話,無非還是上面說的那兩種,外側子孫和內側子孫;
註意:這裡的內側子孫和外側子孫,不是指新插入的節點,而是兩個連續紅色節點中的子節點。。。。也就是下麵第二個圖中的節點10就是爺爺節點50的外側子孫
這樣說起來比較抽象,我們來實際看看兩個例子就ok了;
外側子孫:假如在向下查找插入點的途中找到瞭如下結構:

對紅黑樹的調整就結束了,有沒有發現經過這種調整之後使得後續插入紅色節點就容易了很多,而且縱觀整棵紅黑樹,紅色節點在慢慢向上運動,直到根節點也被調整成紅色,最終我們只需要把根節點變成黑色就好! 插入節點2就不用多說了吧!
內側子孫:這個我是在不想說了,偷個懶,嘿嘿嘿!其實和前面一樣的,就是先改變兩個連續紅節點的子節點和爺爺節點的顏色,然後繞父節點左旋,最後繞爺爺節點右旋,換湯不換藥;
4.總結重點
我們把這篇的重點提出來,其實就是分為插入前和插入後兩步:
(1).插入前我們必須調整一下有隱患的結構,具體操作:當一個黑色節點有兩個紅色節點的時候,我們就改變這三個節點的顏色,紅變黑,黑變紅;但是由於這個黑色節點的父節點可能是黑色,也可能是紅色
當黑色節點的父節點是黑色的時候,那麼這個改變顏色不會造成任何影響
當黑色節點的父節點是紅色的時候,改變顏色之後就會違反紅黑樹規則三,有連續的兩個紅色節點,我們就需要進行旋轉,對於旋轉,我們有兩種情況
第一種,假如兩個連續的紅色節點的子節點是外側子孫,那麼就先改變父節點和爺爺節點的顏色,然後以這個外側子孫的爺爺節點進行右旋
第二種,假如兩個連續的紅色節點的子節點是內側子孫,那麼就先改變內側子孫和爺爺節點的顏色,然後先繞內側子孫的父節點進行左旋,最後繞爺爺節點右旋;
(2)插入節點之後,假如插入的是黑色節點下麵,那沒有什麼改變;假如是插入在紅色節點之下,那麼就會違反紅黑樹規則三,兩個連續的紅色節點,此時就會有兩種調整方式:
第一種,假如這個新插入的節點是外側子孫,那麼改變父節點和爺爺節點的顏色,然後繞著爺爺節點進行右旋
第二種,假如這個新插入的節點是內側子孫,那麼改變當前插入節點和爺爺節點的顏色,再繞著父節點左旋,再繞著爺爺節點右旋
5.代碼
看看前面的邏輯賊多,所以代碼的話最好心裡準備,下麵我們就用java代碼來看一下紅黑樹添加節點的過程;
為什麼暫時不說刪除紅黑樹節點呢?因為刪除節點有點兒複雜,後面有時間再說吧!而且刪除的分為真正的刪除和偽刪除,真正的刪除就是慢慢研究每一個刪除的步驟每一步代碼,從樹中刪除節點;而偽刪除其實就是在節點類中加一個boolean變數,標識該節點是否為已刪除節點,偽刪除其實避免了刪除紅黑樹的全部複雜的邏輯,很容易,但是缺陷也很大,因為刪除的節點還保存在樹中。。。
emmm....本來想自己實現一下的,然而看到一些大佬的博客實現代碼,瞬間感覺自己的代碼很醜陋,就借用一下大佬的代碼;
節點類

public class RBTree<T extends Comparable<T>> { private RBTNode<T> mRoot; // 根結點 private static final boolean RED = false; private static final boolean BLACK = true; public class RBTNode<T extends Comparable<T>> { boolean color; // 顏色 T key; // 關鍵字(鍵值) RBTNode<T> left; // 左孩子 RBTNode<T> right; // 右孩子 RBTNode<T> parent; // 父結點 public RBTNode(T key, boolean color, RBTNode<T> parent, RBTNode<T> left, RBTNode<T> right) { this.key = key; this.color = color; this.parent = parent; this.left = left; this.right = right; } } ... }View Code
右旋

/* * 對紅黑樹的節點(y)進行右旋轉 * * 右旋示意圖(對節點y進行左旋): * py py * / / * y x * / \ --(右旋)-. / \ # * x ry lx y * / \ / \ # * lx rx rx ry * */ private void rightRotate(RBTNode<T> y) { // 設置x是當前節點的左孩子。 RBTNode<T> x = y.left; // 將 “x的右孩子” 設為 “y的左孩子”; // 如果"x的右孩子"不為空的話,將 “y” 設為 “x的右孩子的父親” y.left = x.right; if (x.right != null) x.right.parent = y; // 將 “y的父親” 設為 “x的父親” x.parent = y.parent; if (y.parent == null) { this.mRoot = x; // 如果 “y的父親” 是空節點,則將x設為根節點 } else { if (y == y.parent.right) y.parent.right = x; // 如果 y是它父節點的右孩子,則將x設為“y的父節點的右孩子” else y.parent.left = x; // (y是它父節點的左孩子) 將x設為“x的父節點的左孩子” } // 將 “y” 設為 “x的右孩子” x.right = y; // 將 “y的父節點” 設為 “x” y.parent = x; }View Code
左旋

/* * 對紅黑樹的節點(x)進行左旋轉 * * 左旋示意圖(對節點x進行左旋): * px px * / / * x y * / \ --(左旋)-. / \ # * lx y x ry * / \ / \ * ly ry lx ly * * */ private void leftRotate(RBTNode<T> x) { // 設置x的右孩子為y RBTNode<T> y = x.right; // 將 “y的左孩子” 設為 “x的右孩子”; // 如果y的左孩子非空,將 “x” 設為 “y的左孩子的父親” x.right = y.left; if (y.left != null) y.left.parent = x; // 將 “x的父親” 設為 “y的父親” y.parent = x.parent; if (x.parent == null) { this.mRoot = y; // 如果 “x的父親” 是空節點,則將y設為根節點 } else { if (x.parent.left == x) x.parent.left = y; // 如果 x是它父節點的左孩子,則將y設為“x的父節點的左孩子” else x.parent.right = y; // 如果 x是它父節點的左孩子,則將y設為“x的父節點的左孩子” } // 將 “x” 設為 “y的左孩子” y.left = x; // 將 “x的父節點” 設為 “y” x.parent = y; }View Code
插入節點

/* * 將結點插入到紅黑樹中 * * 參數說明: * node 插入的結點 // 對應《演算法導論》中的node */ private void insert(RBTNode<T> node) { int cmp; RBTNode<T> y = null; RBTNode<T> x = this.mRoot; // 1. 將紅黑樹當作一顆二叉查找樹,將節點添加到二叉查找樹中。 while (x != null) { y = x; cmp = node.key.compareTo(x.key); if (cmp < 0) x = x.left; else x = x.right; } node.parent = y; if (y!=null) { cmp = node.key.compareTo(y.key); if (cmp < 0) y.left = node; else y.right = node; } else { this.mRoot = node; } // 2. 設置節點的顏色為紅色 node.color = RED; // 3. 將它重新修正為一顆二叉查找樹 insertFixUp(node); } /* * 新建結點(key),並將其插入到紅黑樹中 * * 參數說明: * key 插入結點的鍵值 */ public void insert(T key) { RBTNode<T> node=new RBTNode<T>(key,BLACK,null,null,null); // 如果新建結點失敗,則返回。 if (node != null) insert(node); } /* * 紅黑樹插入修正函數 * * 在向紅黑樹中插入節點之後(失去平衡),再調用該函數; * 目的是將它重新塑造成一顆紅黑樹。 * * 參數說明: * node 插入的結點 // 對應《演算法導論》中的z */ private void insertFixUp(RBTNode<T> node) { RBTNode<T> parent, gparent; // 若“父節點存在,並且父節點的顏色是紅色” while (((parent = parentOf(node))!=null) && isRed(parent)) { gparent = parentOf(parent); //若“父節點”是“祖父節點的左孩子” if (parent == gparent.left) { // Case 1條件:叔叔節點是紅色 RBTNode<T> uncle = gparent.right; if ((uncle!=null) && isRed(uncle)) { setBlack(uncle); setBlack(parent); setRed(gparent); node = gparent; continue; } // Case 2條件:叔叔是黑色,且當前節點是右孩子 if (parent.right == node) { RBTNode<T> tmp; leftRotate(parent); tmp = parent; parent = node; node = tmp; } // Case 3條件:叔叔是黑色,且當前節點是左孩子。 setBlack(parent); setRed(gparent); rightRotate(gparent); } else { //若“z的父節點”是“z的祖父節點的右孩子” // Case 1條件:叔叔節點是紅色 RBTNode<T> uncle = gparent.left; if ((uncle!=null) && isRed(uncle)) { setBlack(uncle); setBlack(parent); setRed(gparent); node = gparent; continue; } // Case 2條件:叔叔是黑色,且當前節點是左孩子 if (parent.left == node) { RBTNode<T> tmp; rightRotate(parent); tmp = parent; parent = node; node = tmp; } // Case 3條件:叔叔是黑色,且當前節點是右孩子。 setBlack(parent); setRed(gparent); leftRotate(gparent); } } // 將根節點設為黑色 setBlack(this.mRoot); }View Code
參考大佬博客:https://www.cnblogs.com/skywang12345/p/3624343.html




