一、引言二、普通演算法演算法A:演算法B:三、較好演算法演算法C:演算法D:四、總結 一、引言 這就是類似求Top(K)問題,什麼意思呢?怎麼在無序數組中找到第幾(K)大元素?我們這裡不考慮海量數據,能裝入記憶體。 二、普通演算法 演算法A: 將數組中的元素升序排序,找到數組下標k 1的元素即可。這是大家最容易想 ...
一、引言二、普通演算法演算法A:演算法B:三、較好演算法演算法C:演算法D:四、總結
一、引言
這就是類似求Top(K)問題,什麼意思呢?怎麼在無序數組中找到第幾(K)大元素?我們這裡不考慮海量數據,能裝入記憶體。
二、普通演算法
演算法A:
將數組中的元素升序排序,找到數組下標k-1的元素即可。這是大家最容易想到的方法,如果使用簡單排序演算法,時間複雜度為O(n^2)。
演算法B:
- 第一步:初始化長度為K的一個數組,先讀入K個元素,將元素降序排序(升序也可以),這時候第K大元素就在最後一個。
- 第二步:讀入下一個元素就與已排序的第K大元素比較,如果大於,則將當前的第K大元素刪掉,並將此元素放到前K-1個正確的位置上(這裡就是簡單的插入排序了。不瞭解插入排序的朋友可以看這裡圖解選擇排序與插入排序)。
- 時間複雜度:第一步採用普通排序演算法時間複雜度是O(k^2);第二步:(N-k)*(k-1) = Nk-k^2+k。所以演算法B的時間複雜度為O(NK)。當k=N/2(向下取整)時,時間複雜度還是O(n^2)。
其實求第K大問題,也可以求反,即求第N-k+1小問題。這是等價的。所以當K=N/2時,是最難的地方,但也很有趣,這時候的K對應的值就是中位數。
三、較好演算法
演算法C:
演算法思想:將數據讀入一個數組,對數組進行buildHeap(我們這裡構建大頂堆),之後對堆進行K次deleteMax操作,第K次的結果就是我們需要的值。(因為是大頂堆,所以數據從大到小排了序,堆排序以後會詳細說)。
現在我們來解決上節遺留的問題,為什麼buildHeap是線性的?不熟悉堆的可以看一下 圖解優先隊列(堆)。我們先來看看代碼實現。
public PriorityQueue(T[] items) {
//當前堆中的元素個數
currentSize = items.length;
//可自行實現聲明
array = (T[]) new Comparable[currentSize +1];
int i = 1;
for (T item : items){
array[i++] = item;
}
buildHeap();
}
private void buildHeap() {
for (int i = currentSize / 2; i > 0; i--){
//堆的下濾方法,可參考上面的鏈接
percolateDown(i);
}
}
圖中初始化的是一顆無序樹,經過7次percolateDown後,得到一個大頂堆。從圖中可以看到,共有9條虛線,每一條對應於2次比較,總共18次比較。為了確定buildHeap的時間界,我們需要統計虛線的條數,這可以通過計算堆中所有節點的高度和得到,它是虛線的最大條數。該和是O(N)。
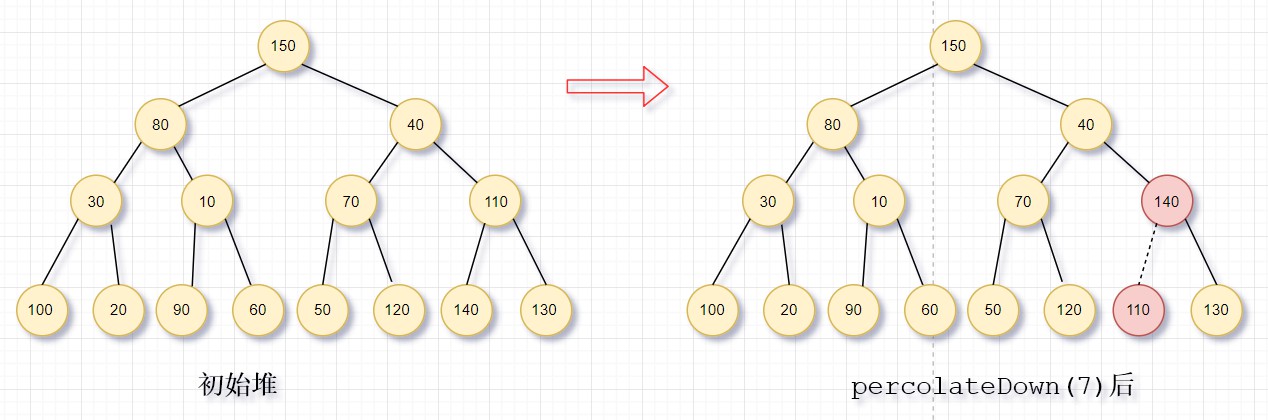


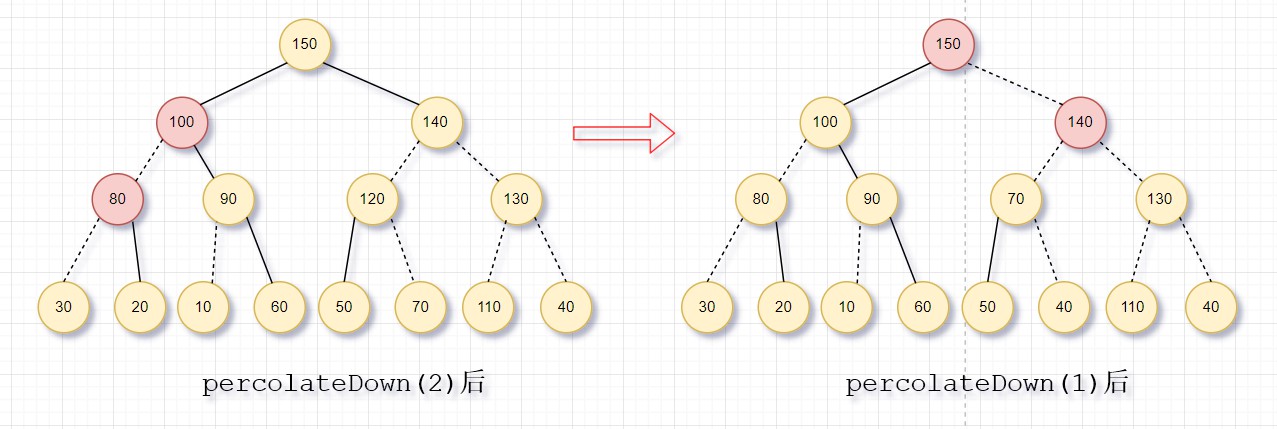
定理:包含2h+1-1個節點、高為h的理想二叉樹(滿二叉樹)的節點的高度的和是2h+1-1-(h+1)。
什麼叫滿二叉樹?滿二叉樹是完全填滿的二叉樹,最後一層都是填滿的,如圖中所示。完全二叉樹,是除最後一層以外都是填滿的,最後一層外也必須從左到右依次填入,就是上一篇中說的堆的結構。滿二叉樹一定是完全二叉樹,完全二叉樹不一定是滿二叉樹。
證明定理:
容易看出,滿二叉樹中,高度為h上,有1個節點;高度h-1上2個節點,高度h-2上有2^2個節點及一般在高度h-i上的2i個節點組成。
方程兩邊乘以2得到:
兩式相減得到:
所以定理得證。因為堆由完全二叉樹構成,所以堆的節點數在2h和2h+1之間,所以意味著這個和是O(N)。所以buildHeap是線性的。所以演算法C的時間複雜度是:初始化數組為O(N),buildHeap為O(N),K次deleeMax需要O(klogN),所以總的時間複雜度是:O(N+N+klogN)=O(N+klogN),如果K為N/2時,運行時間是O(NlogN)。
演算法D:
- 演算法思想:我們採用演算法B的思想,只是我們這裡構建一個節點數為K的小頂堆,只要下一個數比根節點大,就刪除根節點,並將這個數進行下濾操作。所以演算法最終的第K大數就是根節點的數。
- 時間複雜度:對K個數進行buildHeap是O(k),最壞情況下假設剩下的N-k個數都要進入堆中進行下濾操作,總的需要O(k+(N-k)logk)。如果K為N/2,則需要O(NlogN)。
四、總結
本篇詳述了 求top(K)問題的幾種解法,前兩種十分平凡普通,後兩種比較優一點,暫時給出求解中位數需要O(NlogN)時間。以後還會介紹更優的方式,可以以平均時間O(N)解決這個問題。



