C / C ++ 基於梯度下降法的線性回歸法（適用於機器學習）

寫在前面的話：

在第一學期做項目的時候用到過相應的知識，覺得挺有趣的，就記錄整理了下來，基於C/C++語言

原貼地址：https://helloacm.com/cc-linear-regression-tutorial-using-gradient-descent/

---------------------------------------------------------------前言----------------------------------------------------------------------------------

在機器學習和數據挖掘處理等領域，梯度下降（Gradient Descent）是一種線性的、簡單卻比較有效的預測演算法。它可以基於大量已知數據進行預測，　並可以通過控制誤差率來確定誤差範圍。

--------------------------------------------------------準備------------------------------------------------------------------------

Gradient Descent

回到主題，線性回歸演算法有很多，但Gradient Descent是最簡單的方法之一。對於線性回歸，先假設數據滿足線性關係，例如：

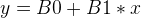
所以，作為線性回歸，我們的任務就是找到最合適 B0 和 B1， 使最後的結果Y滿足可接受的準確度。作為起步，首先讓我們對B0和B1賦值初始值0，如下所示：

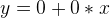
設誤差 Error 為 e， 並引入下麵幾個點做例子：

x y
1 1
2 3
4 3
3 2
5 5

如果我們計算第一個點的誤差，則得到 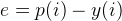，其中P（i）為表中的數據值，則 e 結果為  -1。但這隻是開始，下麵我們可以使用Gradient Descent來更新Y中的繫數。這就涉及到數據 / 機器學習， 所謂的 數據 / 機器學習，其實可以大致理解為在相應的函數模型下，通過不停地更新其中繫數，使新函數曲線可以擬合原始數據並預測走勢的過程。

回到主題，設剛纔的初始狀態為 t ，那麼對於下一個狀態 t+1 ， B0可表示為 ：

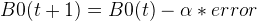
其中 B0（t + 1）是繫數的更新版本，為套入下一個點做準備。∂ 是學習率，即為精度，這個我們可以自己設定。∂ 越大，說明每次學習的跨度就越大，預測結果在相應的正確答案兩邊的擺幅也就越大，所以此情況下學習次數不易過多，否則越擺越離譜。Ps:有次因為∂ 值太大的原因導致結果不精準，結過以為是學習次數不夠多，後來等到把2.3的數值擺到10個億才反應過來是∂出來問題。話說10個億真是個小目標呢。

言歸正傳，這裡取 ∂ = 0.01，即可得以下式子，B0=0.01.

.

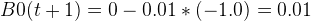現在再來看 B1，在 t+1時刻，公式變為：

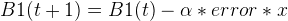
同樣賦值，也同樣得到：

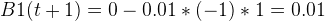
--------------------------------------------------------操作------------------------------------------------------------------------

現在，我們可以重覆迭代這種過程到下一個點，再到下下個點，一直到所有點結束，這稱為1回（an epoch）。但是我們可以通過反覆不停地迭代，來使得到的線性擬合曲線更接近初始數據。比如迭代4回，每回5個點，也就是20次。C / C ++代碼如下：

double x[] = {1, 2, 4, 3, 5};
double y[] = {1, 3, 3, 2, 5};
 
double b0 = 0;
double b1 = 0;
double alpha = 0.01;
 
for (int i = 0; i < 20; i ++) {
    int idx = i % 5; //5個點
    double p = b0 + b1 * x[idx];
    double err = p - y[idx];
    b0 = b0 - alpha * err;
    b1 = b1 - alpha * err * x[idx];
}

把B0、B1還有 誤差（Error）的結果列印出來：

B0 = 0.01, B1 = 0.01, err = -1
B0 = 0.0397, B1 = 0.0694, err = -2.97
B0 = 0.066527, B1 = 0.176708, err = -2.6827
B0 = 0.0805605, B1 = 0.218808, err = -1.40335
B0 = 0.118814, B1 = 0.410078, err = -3.8254
B0 = 0.123526, B1 = 0.414789, err = -0.471107
B0 = 0.143994, B1 = 0.455727, err = -2.0469
B0 = 0.154325, B1 = 0.497051, err = -1.0331
B0 = 0.157871, B1 = 0.507687, err = -0.354521
B0 = 0.180908, B1 = 0.622872, err = -2.3037
B0 = 0.18287, B1 = 0.624834, err = -0.196221
B0 = 0.198544, B1 = 0.656183, err = -1.56746
B0 = 0.200312, B1 = 0.663252, err = -0.176723
B0 = 0.198411, B1 = 0.65755, err = 0.190068
B0 = 0.213549, B1 = 0.733242, err = -1.51384
B0 = 0.214081, B1 = 0.733774, err = -0.0532087
B0 = 0.227265, B1 = 0.760141, err = -1.31837
B0 = 0.224587, B1 = 0.749428, err = 0.267831
B0 = 0.219858, B1 = 0.735242, err = 0.472871
B0 = 0.230897, B1 = 0.790439, err = -1.10393

怎麼樣，能發現什麼？不容易看出來沒關係，我們把點畫下來：

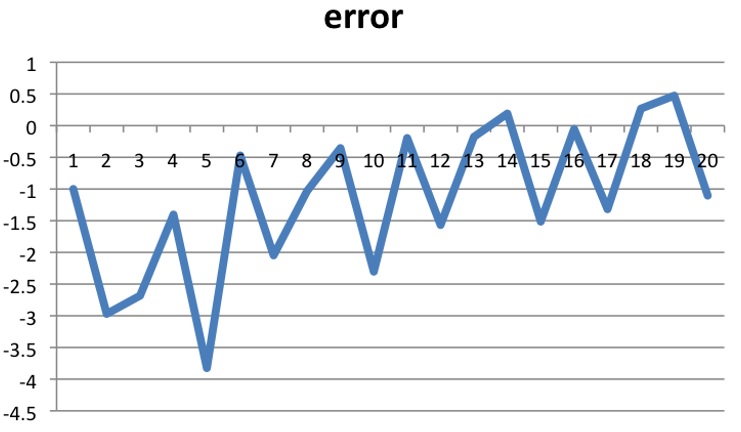
從圖中，我們可以看到誤差正逐漸變小，所以我們的最終模型也就是第20次的模型：

所以最後的曲線擬合結果如下：

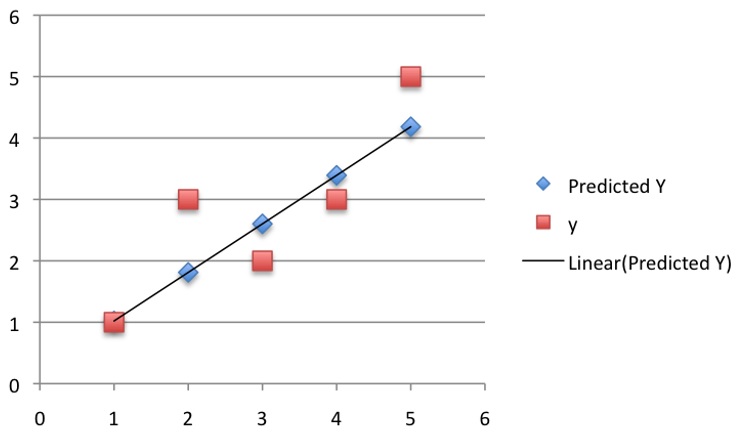
到這裡其實不一定死板地局限於20次，也並不是迭代次數越多越好，因為這個過程像一個開口向下的二次函數， 適合的才是最好的。

因為最合適的點可能就在中間，迭代太多次就跑偏了。解決這個問題可以在源代碼里簡單地加一個 If () 函數，當誤差滿足xxx時跳出迴圈就完事了。

到這裡應該就結束了。但原文章里多算了一次 Root-Mean-Square 值，也就是均方根，常用來分析雜訊或者誤差，公式如下：

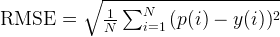   把每個點帶入，得到RMSE=0.72。

--------------------------------------------------------總結------------------------------------------------------------------------

其實Gradient Descent 通常適用於 量非常大且繁瑣的數據（不在乎有那麼幾個因為跑偏而被淘汰的值）。

但如果要求數據足夠精確、且數據模型複雜，不適合一次函數模型，那Gradient Descent  並不見得是一個好方法。