Treap詳解 Treap=Tree+Heap Treap中每個節點有2個值，其中一個滿足二叉查找樹的性質，一個滿足大根堆的性質。把滿足二叉查找樹性質的值稱作，把滿足大根堆性質的值稱作。對於Treap來說，當前節點的值大於左兒子，小於右兒子。當前節點的值小於兒子節點的值。每個節點的我們 ...

Treap詳解

Treap=Tree+Heap

Treap中每個節點有2個值，其中一個滿足二叉查找樹的性質，一個滿足大根堆的性質。把滿足二叉查找樹性質的值稱作data，把滿足大根堆性質的值稱作value。對於Treap來說，當前節點的data值大於左兒子，小於右兒子。當前節點的value值小於兒子節點的值。
每個節點的data我們無法改變，為了保證Treap的平衡性，我們需要讓每個節點的value均為隨機值，這樣我們就可以保證這棵樹“基本平衡”。

統計

\(up\)：計算兒子數

void up(int x)
{
    t[x].siz=t[t[x].left].siz+t[t[x].right].siz+1;
}

旋轉

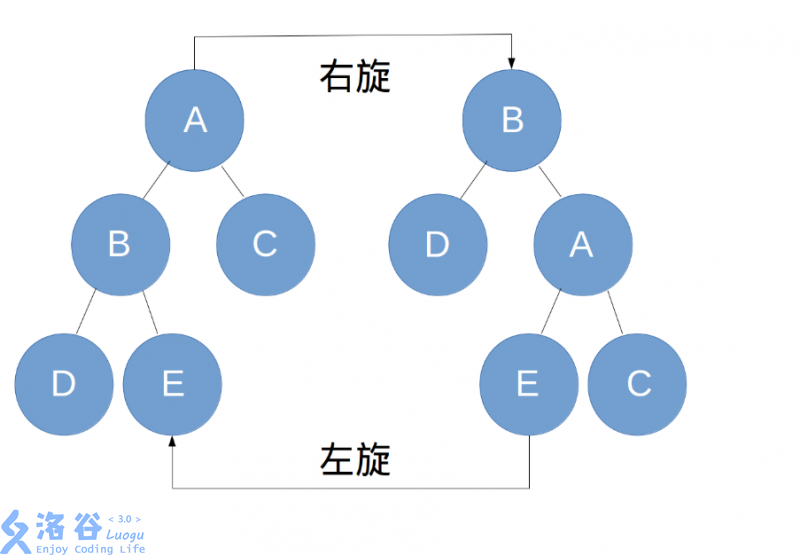
rorate
右旋就是，讓當前節點降為自己的右兒子，讓左兒子代替自己，並讓自己左兒子的右兒子成為自己的左兒子。
左旋相反，讓當前節點降為自己的左兒子，讓右兒子代替自己，並讓自己右兒子的左兒子成為自己的右兒子。
註：代碼中的now加上了&是為了可以在函數中同時更改now的值。如上圖右旋時，原來now指向\(A\)節點，運行完函數後指向\(B\)節點。

void right_rorate(int &now)
{
    int tmp=t[now].left;
    t[now].left=t[tmp].right;
    t[tmp].right=now;
    t[tmp].siz=t[now].siz;
    up(now);
    now=tmp;
}
void left_rorate(int &now)
{
    int tmp=t[now].right;
    t[now].right=t[tmp].left;
    t[tmp].left=now;
    t[tmp].siz=t[now].siz;
    up(now);
    now=tmp;
}

旋轉實例：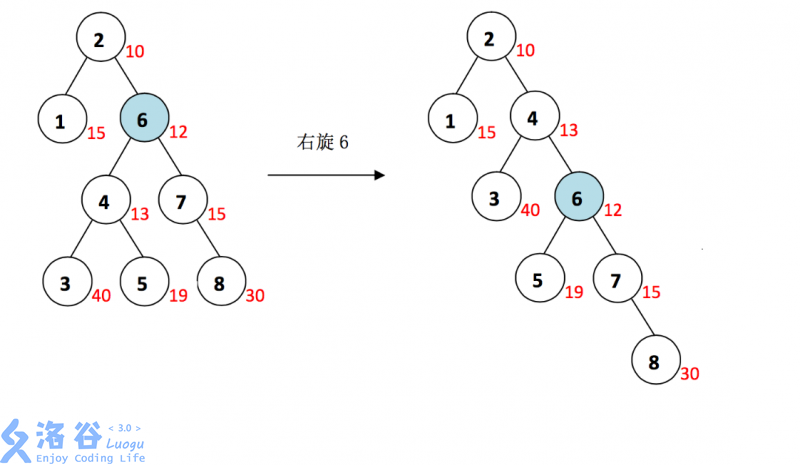
eg2

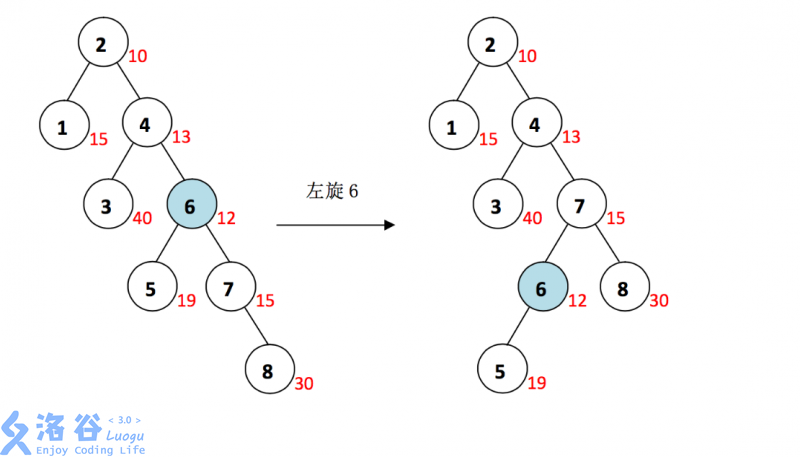
插入

給節點隨機分配一個優先順序(value)，先把要插入的點插入到一個葉子上，然後跟維護堆一樣，我們維護一個 小根堆，如果當前節點的優先順序比它的兒子大就旋轉，如果當前節點是根的左兒子就右旋，如果當前節點是根的右兒子就左旋。

void insert(int &now,int data)
{
    if(now==0)
    {
        now=++cnt;
        t[now].siz=1;
        t[now].data=data;
        t[now].value=rand()*rand()%19620817;
        return ;
    }
    t[now].siz++;
    if(data>=t[now].data)
    {
        insert(t[now].right,data);
    }
    else
    {
        insert(t[now].left,data);
    }
    if(t[now].left!=0&&t[now].value>t[t[now].left].value)
    {
        right_rorate(now);
    }
    if(t[now].right!=0&&t[now].value>t[t[now].right].value)
    {
        left_rorate(now);
    }
    up(now);
}

刪除

因為\(Treap\)滿足堆性質，所以只需要把要刪除的節點旋轉到葉節點上，然後直接刪除就可以了。
具體的方法：
如果該節點的左子節點的優先順序小於右子節點的優先順序，右旋該節點，使該節點降為右子樹的根節點，然後訪問右子樹的根節點，繼續操作；
反之，左旋該節點,使該節點降為左子樹的根節點，然後訪問左子樹的根節點，繼續操作，直到變成可以直接刪除的節點。
（即：讓value的結點旋到上面，滿足堆的性質）

void erase(int &now,int data)
{
    t[now].siz--;
    if(t[now].data==data)
    {
        if(t[now].left==0&&t[now].right==0)
        {
            now=0;
            return ;
        }
        if(t[now].left==0||t[now].right==0)
        {
            now=t[now].left+t[now].right;
            return ;
        }
        if(t[t[now].left].value<t[t[now].right].value)
        {
            right_rorate(now);
            erase(t[now].right,data);
            return ;
        }
        else
        {
            left_rorate(now);
            erase(t[now].left,data);
            return ;
        }
    }
    if(t[now].data>=data)
    {
        erase(t[now].left,data);
    }
    else
    {
        erase(t[now].right,data);
    }
    up(now);
}

查詢排名

顯然，若t[now].data<data，則在now的右子樹中仍有部分小於data的數，所以在加上t[t[now].left].siz+1的同時還需在now的右子樹中繼續遞歸。反之，則只需在左子樹中遞歸

int rank(int now,int data)
{
    if(now==0)
    {
        return 0;
    }
    if(data>t[now].data)
    {
        return t[t[now].left].siz+1+rank(t[now].right,data);
    }
    return rank(t[now].left,data);
}

查詢排名為\(x\)的數

若左子樹的大小剛好為\(x-1\)，則當前節點的data即為所求結果。
若左子樹的大小大於\(x-1\)，則在右子樹中遞歸查找。
若左子樹的大小小於\(x-1\)，則在左子樹中遞歸查找。

int find(int now,int rank)
{
    if(rank==t[t[now].left].siz+1)
    {
        return t[now].data;
    }
    if(rank>t[t[now].left].siz+1)
    {
        return find(t[now].right,rank-t[t[now].left].siz-1);
    }
    return find(t[now].left,rank);
}

查詢前驅

函數定義：

int query_pre(int now,int data)

若now==0，則不存在返回值（return 0）。
若當前節點的值大於等於data，則在右子樹中找。（必須包含等於！！！）
若當前節點的值小於data，則在左子樹中找，若找不到，則返回當前節點的值。（不能有等於！！！）

int query_pre(int now,int data)
{
    if(now==0)
    {
        return 0;
    }
    if(t[now].data>=data)
    {
        return query_pre(t[now].left,data);
    }
    int tmp=query_pre(t[now].right,data);
    if(tmp==0)
    {
        return t[now].data;
    }
    return tmp;
}

查詢後繼

與前驅幾乎相同（略）

int query_suf(int now,int data)
{
    if(now==0)
    {
        return 0;
    }
    if(t[now].data<=data)
    {
        return query_suf(t[now].right,data);
    }
    int tmp=query_suf(t[now].left,data);
    if(tmp==0)
    {
        return t[now].data;
    }
    return tmp;
}

洛谷P3369完整代碼：

#include<bits/stdc++.h>
using namespace std;
struct Treap
{
    int data;
    int value;
    int left;
    int right;
    int siz;
};
Treap t[100005];
int cnt;
int root;
void up(int x)
{
    t[x].siz=t[t[x].left].siz+t[t[x].right].siz+1;
}
void right_rorate(int &now)
{
    int tmp=t[now].left;
    t[now].left=t[tmp].right;
    t[tmp].right=now;
    t[tmp].siz=t[now].siz;
    up(now);
    now=tmp;
}
void left_rorate(int &now)
{
    int tmp=t[now].right;
    t[now].right=t[tmp].left;
    t[tmp].left=now;
    t[tmp].siz=t[now].siz;
    up(now);
    now=tmp;
}
void insert(int &now,int data)
{
    if(now==0)
    {
        now=++cnt;
        t[now].siz=1;
        t[now].data=data;
        t[now].value=rand()*rand()%19620817;
        return ;
    }
    t[now].siz++;
    if(data>=t[now].data)
    {
        insert(t[now].right,data);
    }
    else
    {
        insert(t[now].left,data);
    }
    if(t[now].left!=0&&t[now].value>t[t[now].left].value)
    {
        right_rorate(now);
    }
    if(t[now].right!=0&&t[now].value>t[t[now].right].value)
    {
        left_rorate(now);
    }
    up(now);
}
void erase(int &now,int data)
{
    t[now].siz--;
    if(t[now].data==data)
    {
        if(t[now].left==0&&t[now].right==0)
        {
            now=0;
            return ;
        }
        if(t[now].left==0||t[now].right==0)
        {
            now=t[now].left+t[now].right;
            return ;
        }
        if(t[t[now].left].value<t[t[now].right].value)
        {
            right_rorate(now);
            erase(t[now].right,data);
            return ;
        }
        else
        {
            left_rorate(now);
            erase(t[now].left,data);
            return ;
        }
    }
    if(t[now].data>=data)
    {
        erase(t[now].left,data);
    }
    else
    {
        erase(t[now].right,data);
    }
    up(now);
}
int rank(int now,int data)
{
    if(now==0)
    {
        return 0;
    }
    if(data>t[now].data)
    {
        return t[t[now].left].siz+1+rank(t[now].right,data);
    }
    return rank(t[now].left,data);
}
int find(int now,int rank)
{
    if(rank==t[t[now].left].siz+1)
    {
        return t[now].data;
    }
    if(rank>t[t[now].left].siz+1)
    {
        return find(t[now].right,rank-t[t[now].left].siz-1);
    }
    return find(t[now].left,rank);
}
int query_pre(int now,int data)
{
    if(now==0)
    {
        return 0;
    }
    if(t[now].data>=data)
    {
        return query_pre(t[now].left,data);
    }
    int tmp=query_pre(t[now].right,data);
    if(tmp==0)
    {
        return t[now].data;
    }
    return tmp;
}
int query_suf(int now,int data)
{
    if(now==0)
    {
        return 0;
    }
    if(t[now].data<=data)
    {
        return query_suf(t[now].right,data);
    }
    int tmp=query_suf(t[now].left,data);
    if(tmp==0)
    {
        return t[now].data;
    }
    return tmp;
}
int main()
{
    srand(19620817);
    int n;
    cin>>n;
    int opt,data;
    for(int i=1;i<=n;i++)
    {
        scanf("%d %d",&opt,&data);
        if(opt==1)
        {
            insert(root,data);
        }
        if(opt==2)
        {
            erase(root,data);
        }
        if(opt==3)
        {
            printf("%d\n",rank(root,data)+1);
        }
        if(opt==4)
        {
            printf("%d\n",find(root,data));
        }
        if(opt==5)
        {
            printf("%d\n",query_pre(root,data));
        }
        if(opt==6)
        {
            printf("%d\n",query_suf(root,data));
        }
    }
    return 0;
}

註：本文部分圖片來自Brave_Cattle的Blog（自己學的時候參考的）

Treap學習筆記