機器學習實戰（筆記）------------KNN演算法

1.KNN演算法 KNN演算法即K 臨近演算法，採用測量不同特征值之間的距離的方法進行分類。以二維情況舉例：假設一條樣本含有兩個特征。將這兩種特征進行數值化，我們就可以假設這兩種特種分別為二維坐標系中的橫軸和縱軸，將一個樣本以點的形式表示在坐標系 ...

1.KNN演算法

KNN演算法即K-臨近演算法，採用測量不同特征值之間的距離的方法進行分類。

以二維情況舉例：

假設一條樣本含有兩個特征。將這兩種特征進行數值化，我們就可以假設這兩種特種分別為二維坐標系中的橫軸和縱軸，將一個樣本以點的形式表示在坐標系中。這樣，兩個樣本直接變產生了空間距離，假設兩點之間越接近越可能屬於同一類的樣本。如果我們有一個待分類數據，我們計算該點與樣本庫中的所有點的距離，取前K個距離最近的點，以這K個中出現次數最多的分類作為待分類樣本的分類。這樣就是KNN演算法。

優點：精度高，對異常值不敏感，無數據輸入假定
缺點：時間、空間複雜度太大（比如每一次分類都需要計算所有樣本點與測試點的距離）

2.KNN演算法的Python實現

import operator
from os import listdir

import matplotlib
import matplotlib.pyplot as plt
from numpy import array, shape, tile, zeros

#分類方法
#inx 待分類向量
#dataSet 測試數據
#labels 測試數據標簽
#k 取前k個作為樣本
def classify(inX,dataSet,labels,k):
    dataSetSize=dataSet.shape[0]
    diffMat=tile(inX,(dataSetSize,1))-dataSet #tile方法利用輸入數組進行擴充
    sqDiffMat=diffMat**2
    sqDistance=sqDiffMat.sum(axis=1)
    distance=sqDistance**0.5
    index=distance.argsort() #返回按從小到大的順序排序後的元素下標
    classCount={}
    for i in range(k):
        lable=labels[index[i]]
        classCount[lable]=classCount.get(lable,0)+1
    #在python3中dict.iteritems()被廢棄
    sortedClasssCount=sorted(classCount.items(),
    key=operator.itemgetter(1),reverse=True)
    return sortedClasssCount[0][0]

代碼傳入的三個參數分別為待分類向量，測試數據，測試數據標簽。代碼使用歐式距離公式計算向量點之間的距離。
\[ d=\sqrt{(xA_0-xB_0)^2-（xA_1-xB_1)^2} \]

numpy.tile(A,reps)

A指待輸入數組，reps則決定A的重覆次數
sorted(iterable,cmp,key,reverse)

這裡利用了key參數使得使用字典中的value值進行排序

實例1：KNN演算法改進約會網站配對效果

背景

假設A在利用約會網站進行約會，她將自己交往過的人分為三類：

不喜歡的人
魅力一般的人
極具魅力的人

A收集這些人的生活記錄，從中提取中三類特征，存儲在文本datingTestSet2中：

每年獲得的飛行常客里程數
玩游戲視頻所耗時間百分比
每周消耗的冰淇淋公升數

利用這三類特征和標簽組成的樣本庫，我們可以在獲得一個人的這三種特征的特征值的情況下，利用KNN演算法判斷該人是否會是A喜歡人

讀取數據

我們將數據從文本中讀出，並且以矩陣的形式進行存儲

def file2matrix(filename):
    fr=open(filename)
    datalines=fr.readlines()
    numberoflines=len(datalines)
    returnMat=zeros((numberoflines,3))
    classlabelVector=[]
    index=0
    for line in datalines:
        line=line.strip()
        listfromline=line.split('\t')
        returnMat[index,:]=listfromline[0:3]
        classlabelVector.append(int(listfromline[-1]))
        index=index+1
    return returnMat,classlabelVector

分析數據

我們可以利用Matplotlib製作原始數據的散點圖，觀察特征

def analydata():
    a,b=file2matrix('datingTestSet2.txt')
    #創建一個圖形實例
    fig=plt.figure()
    ax=fig.add_subplot(111)
    #scatter方法創建散點圖
    #分析圖像可以發現使用第一列和第二列數據特征更加明顯
    ax.scatter(a[:,0],a[:,1],15.0*array(b),15.0*array(b))
    plt.show()

畫圖結果：

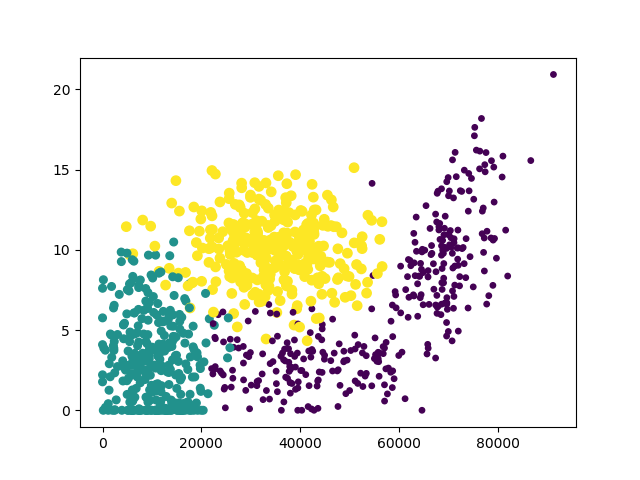
這裡以“冰淇淋公斤數”和“玩視頻游戲所耗時間百分比”作為橫縱坐標特征最為明顯

歸一化數據

在數據分析和機器學習中，經常要進行數據歸一化。因為不同的特征值使用不同的量度，上下限不同，使得有的特征產生的差值很大，而有的很小，會影響演算法準確性。所以要先對數據預處理，進行數據歸一化處理。
\[ newValue=(oldValue-min)/(max-min) \]

分類器與測試

我們利用KNN演算法，以前10%的數據作為待分類數據，後90%的數據作為樣本庫測試數據，進行分類與測試

def datingClassTest():
    hoRatio=0.10
    datingDataMat,datingLables=file2matrix('datingTestSet2.txt')
    normMat=data2normal(datingDataMat)
    m=normMat.shape[0]
    numTestVecs=int(hoRatio*m)
    errorCount=0
    for i in range(numTestVecs):
        result=classify(normMat[i,:],normMat[numTestVecs:m,:],
        datingLables[numTestVecs:m],3)
        print("the classify come back with: %d,the real answer is: %d"
        %(result,datingLables[i]))
        if(result!=datingLables[i]):
            errorCount+=1.0
    print("error rate is:%f"%(errorCount/float(numTestVecs)))

測試結果，錯誤率大概在5%左右。
我們可以改變hoRatio和k的值，檢查錯誤率是否發生變化

實例2：手寫識別系統

背景

假設我們有一些手寫數字，以如下形式保存：

00000000000001100000000000000000
00000000000011111100000000000000
00000000000111111111000000000000
00000000011111111111000000000000
00000001111111111111100000000000
00000000111111100011110000000000
00000001111110000001110000000000
00000001111110000001110000000000
00000011111100000001110000000000
00000011111100000001111000000000
00000011111100000000011100000000
00000011111100000000011100000000
00000011111000000000001110000000
00000011111000000000001110000000
00000001111100000000000111000000
00000001111100000000000111000000
00000001111100000000000111000000
00000011111000000000000111000000
00000011111000000000000111000000
00000000111100000000000011100000
00000000111100000000000111100000
00000000111100000000000111100000
00000000111100000000001111100000
00000000011110000000000111110000
00000000011111000000001111100000
00000000011111000000011111100000
00000000011111000000111111000000
00000000011111100011111111000000
00000000000111111111111110000000
00000000000111111111111100000000
00000000000011111111110000000000
00000000000000111110000000000000

這是一個32*32的矩陣，利用0代表背景，1來代表手寫數字
對於這些數據，我們也可以利用KNN演算法來識別寫的是0~9中的哪裡數字
註：存儲數據的文件，例如：0_0.txt代碼數字0的第一個手寫樣本數據

數據預處理：轉換成測試向量

數據使用32X32的矩陣形式存儲，為了能夠使用我們實現的KNN分類器，我們必須將其轉化成1X1024的向量形式進行表示，也可以叫做降維，將二維數據轉換成了一維數據

def img2vector(filename):
    fr=open(filename)
    returnVect=zeros((1,1024))
    for i in range(32):
        linestr=fr.readline()
        for j in range(32):
            returnVect[0,i*32+j]=int(linestr[j])
    return returnVect

使用KNN演算法進行分類

轉換成向量以後，我們就可以使用我們實現的KNN分類器進行分類了

import operator
from os import listdir

import matplotlib
import matplotlib.pyplot as plt
from numpy import array, shape, tile, zeros

def handwritingClassTest():
    hwlabels=[]
    traingfilelist=listdir('digits/trainingDigits')
    m=len(traingfilelist)
    trainingDataMat=zeros((m,1024))
    for i in range(m):
        filenameStr=traingfilelist[i]
        fileStr=filenameStr.split('.')[0]
        label=int(fileStr.split('_')[0])
        hwlabels.append(label)
        trainingDataMat[i,:]=img2vector
        ('digits/trainingDigits/%s' % filenameStr)
    errorCount=0.0
    testfilelist=listdir('digits/testDigits')
    mTest=len(testfilelist)
    for i in range(mTest):
        filenameStr=testfilelist[i]
        fileStr=filenameStr.split('.')[0]
        label=int(fileStr.split('_')[0])
        testVector=img2vector('digits/testDigits/%s' %filenameStr)
        result=classify(testVector,trainingDataMat,hwlabels,3)
        print('come back with: %d,the real answer is: %d' % (int(result),label))
        if(int(result)!=label):
            errorCount=errorCount+1.0
    print('total number errors is :%f' % errorCount)
    print('error rate is :%f'% (errorCount/float(mTest)))

os.listdir()

利用該方法，可以得到指定目錄裡面的所有文件名