演算法基礎 \(\text{Update: 2024 - 07 - 22}\) 複雜度 定義 衡量一個演算法的快慢,一定要考慮數據規模的大小。 一般來說,數據規模越大,演算法的用時就越長。 而在演算法競賽中,我們衡量一個演算法的效率時,最重要的不是看它在某個數據規模下的用時,而是看它的用時隨數據規模而增長的趨 ...
演算法基礎
\(\text{Update: 2024 - 07 - 22}\)
複雜度
定義
衡量一個演算法的快慢,一定要考慮數據規模的大小。
一般來說,數據規模越大,演算法的用時就越長。
而在演算法競賽中,我們衡量一個演算法的效率時,最重要的不是看它在某個數據規模下的用時,而是看它的用時隨數據規模而增長的趨勢,即時間複雜度。
符號定義
相等是 \(\Theta\),小於是 \(O\),大於是 \(\Omega\)。
大 \(\Theta\) 符號
對於函數 \(f(n)\) 和 \(g(n)\),\(f(n)=\Theta(g(n))\),當且僅當 \(\exists c_1,c_2,n_0>0\),使得 \(\forall n \ge n_0, 0\le c_1\cdot g(n)\le f(n) \le c_2\cdot g(n)\)。
大 \(O\) 符號
\(\Theta\) 符號同時給了我們一個函數的上下界,如果只知道一個函數的漸進上界而不知道其漸進下界,可以使用 \(O\) 符號。\(f(n) = O(g(n))\),當且僅當 \(\exists c,n_0\),使得 \(\forall n \ge n_0,0\le f(n)\le c\cdot g(n)\)。
研究時間複雜度時通常會使用 \(O\) 符號,因為我們關註的通常是程式用時的上界,而不關心其用時的下界。
大 \(\Omega\) 符號
同樣的,我們使用 \(\Omega\) 符號來描述一個函數的漸進下界。\(f(n) = \Omega(g(n))\),當且僅當 \(\exists c, n_0\),使得 \(\forall n \ge n_0, 0 \le c \cdot g(n) \le f(n)\)。
主定理
建議背下來,不是很好理解。
\[T(n) = aT(\frac{n}{b}) + f(n) \qquad \forall n > b \]那麼
\[T(n) = \begin{cases} \Theta(n^{\log_b a}) & f(n) = O(n^{\log_b (a) - \epsilon}), \epsilon > 0 \\ \Theta(f(n)) & f(n) = \Omega(n^{\log_b (a) + \epsilon}), \epsilon\ge 0\\ \Theta(n^{\log_b a} \log^{k+1} n) & f(n) = \Theta(n^{\log_b a} \log^k n), k \ge 0 \end{cases} \]需要註意的是,這裡的第二種情況還需要滿足 \(\text{regularity condition}\), 即 \(a f(n/b) \leq c f(n)\),\(\text{for some constant}\) \(c < 1\) \(\text{and sufficiently large}\) \(n\)。
幾個例子:
-
\(T(n) = 2T(\frac{n}{2}) + 1\),那麼 \(a = 2, b = 2, {\log_2 2} = 1\),那麼 \(\epsilon\) 可以取值在 \((0, 1]\) 之間,從而滿足第一種情況,所以 \(T(n) = \Theta(n)\)。
-
\(T(n) = T(\frac{n}{2}) + n\),那麼 \(a = 1, b = 2, {\log_2 1} = 0\),那麼 \(\epsilon\) 可以取值在 \((0, 1]\) 之間,從而滿足第二種情況,所以 \(T(n) = \Theta(n)\)。
-
\(T(n) = T(\frac{n}{2}) + {\log n}\),那麼 \(a = 1, b = 2, {\log_2 1} = 0\),那麼 \(k\) 可以取值為 \(1\),從而滿足第三種情況,所以 \(T(n) = \Theta(\log^2 n)\)。
-
\(T(n) = T(\frac{n}{2}) + 1\),那麼 \(a = 1, b = 2, {\log_2 1} = 0\),那麼 \(k\) 可以取值為 \(0\),從而滿足第三種情況,所以 \(T(n) = \Theta(\log n)\)。
空間複雜度
類似地,演算法所使用的空間隨輸入規模變化的趨勢可以用空間複雜度來衡量。
枚舉
實際上一些題的正解就是枚舉,但需要很多優化。
要點:
-
建立簡潔的數學模型。
-
減少不必要的枚舉空間。
-
選擇合適的枚舉順序。
模擬
模擬即為將題目描述中的操作用代碼實現,碼量一般比較大,寫錯比較難調,相當浪費時間。
寫模擬題時有以下註意的點:
-
在寫代碼之前,儘量在演草紙上自習分析題目的實現過程。
-
在代碼中儘量把每個部分抽離出來寫成函數,模塊化。
-
將題目中的信息轉化,不要殘留多種表達。
-
如果一次沒過大樣例,分塊調試。
-
實現代碼時按照演草紙上的思路一步步實現。
遞歸
定義
我們可以用以下代碼理解遞歸:
long long f(傳入數值) {
if(終止條件) return 最小子問題解;
return f(縮小問題規模);
}
遞歸的優點
- 結構清晰、可讀性強,可以參考歸併排序的兩種實現方式。
- 練習分析為題的結構,當發現問題可以分解成相同結構的小問題時,遞歸寫多了就能敏銳發現這個特點,進而高效解決問題。
遞歸的缺點
在程式執行中,遞歸是利用堆棧來實現的。每當進入一個函數調用,棧就會增加一層棧幀,每次函數返回,棧就會減少一層棧幀。而棧不是無限大的,當遞歸層數過多時,就會造成棧溢出 的後果。
顯然有時候遞歸處理是高效的,比如歸併排序;有時候是低效的,比如數孫悟空身上的毛,因為堆棧會消耗額外空間,而簡單的遞推不會消耗空間。比如這個例子,給一個鏈表頭,計算它的長度:
// 典型的遞推遍歷框架
int size(Node *head) {
int size = 0;
for (Node *p = head; p != nullptr; p = p->next) size++;
return size;
}
// 我就是要寫遞歸,遞歸天下第一
int size_recursion(Node *head) {
if (head == nullptr) return 0;
return size_recursion(head->next) + 1;
}
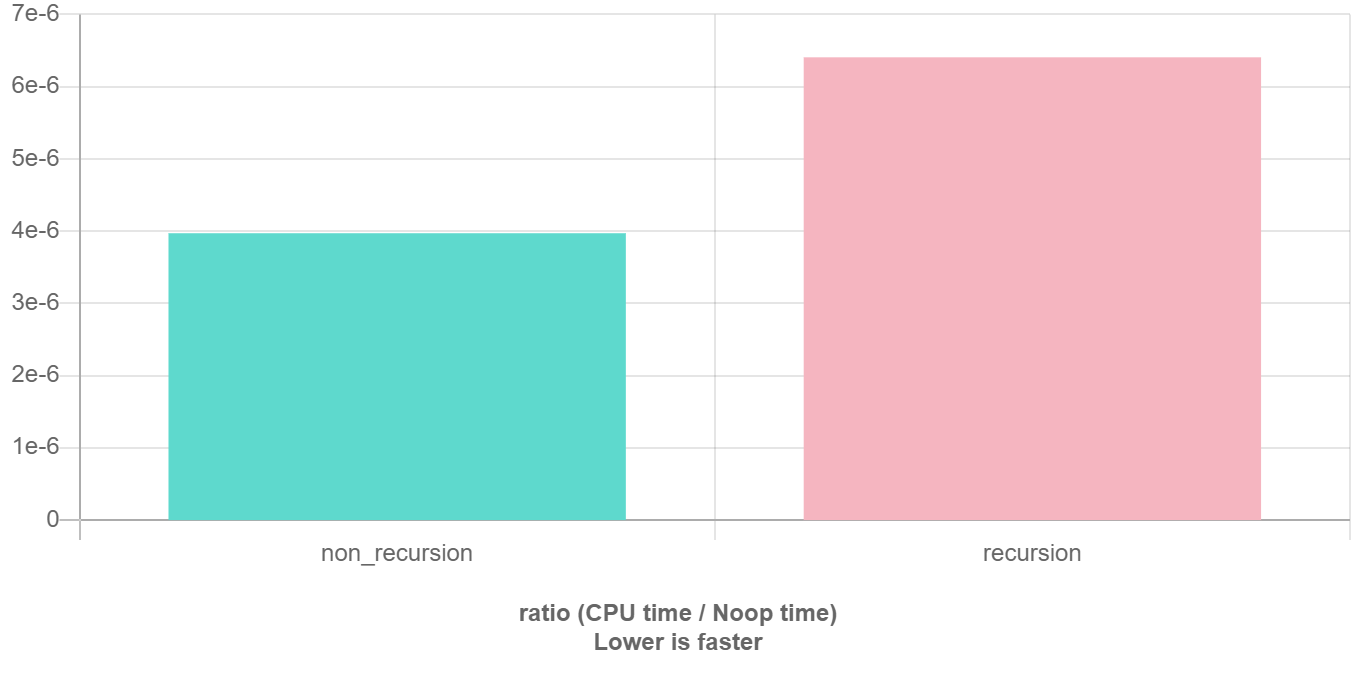
遞歸優化見後文搜索優化和記憶化搜索。
要點
明白一個函數的作用並相信它能完成這個任務,千萬不要跳進這個函數裡面企圖探究更多細節,否則就會陷入無窮的細節無法自拔,人腦能壓幾個棧啊。
遞歸與枚舉的區別
枚舉是橫向地把問題劃分,然後依次求解子問題;而遞歸是把問題逐級分解,是縱向的拆分。
遞歸與分治的區別
遞歸是一種編程技巧,一種解決問題的思維方式;分治演算法很大程度上是基於遞歸的,解決更具體問題的演算法思想。
分治
定義
就是把一個複雜的問題分成兩個或更多的相同或相似的子問題,直到最後子問題可以簡單的直接求解,原問題的解即子問題的解的合併。
過程
分治演算法的核心思想就是「分而治之」。
大概的流程可以分為三步:分解 \(\to\) 解決 \(\to\) 合併。
-
分解原問題為結構相同的子問題。
-
分解到某個容易求解的邊界之後,進行遞歸求解。
-
將子問題的解合併成原問題的解。
分治法能解決的問題一般有如下特征:
-
該問題的規模縮小到一定的程度就可以容易地解決。
-
該問題可以分解為若幹個規模較小的相同問題,即該問題具有最優子結構性質,利用該問題分解出的子問題的解可以合併為該問題的解。
-
該問題所分解出的各個子問題是相互獨立的,即子問題之間不包含公共的子問題。
註意:如果各子問題是不獨立的,則分治法要重覆地解公共的子問題,也就做了許多不必要的工作。此時雖然也可用分治法,但一般用動態規劃較好。
貪心
適用範圍
貪心演算法在有最優子結構的問題中尤為有效。
最優子結構的意思是問題能夠分解成子問題來解決,子問題的最優解能遞推到最終問題的最優解。
證明
貪心演算法有兩種證明方法:反證法和歸納法。
一般情況下,一道題只會用到其中的一種方法來證明。
-
反證法:如果交換方案中任意兩個元素/相鄰的兩個元素後,答案不會變得更好,那麼可以推定目前的解已經是最優解了。
-
歸納法:先算得出邊界情況(例如 \(n = 1\))的最優解 \(F_1\),然後再證明:對於每個 \(n\),\(F_{n + 1}\) 都可以由 \(F_{n}\) 推導出結果。
常見題型
在提高組難度以下的題目中,最常見的貪心有兩種。
-
「我們將 \(XXX\) 按照某某順序排序,然後按某種順序(例如從小到大)選擇。」。
-
「我們每次都取 \(XXX\) 中最大/小的東西,並更新 \(XXX\)。」(有時「\(XXX\) 中最大/小的東西」可以優化,比如用優先隊列維護)
二者的區別在於一種是離線的,先處理後選擇;一種是線上的,邊處理邊選擇。
排序解法
用排序法常見的情況是輸入一個包含幾個(一般一到兩個)權值的數組,通過排序然後遍歷模擬計算的方法求出最優值。
後悔解法
思路是無論當前的選項是否最優都接受,然後進行比較,如果選擇之後不是最優了,則反悔,捨棄掉這個選項;否則,正式接受。如此往複。
排序
幾種排序演算法的比較
一張表格速通
| 排序方法 | 平均情況 | 最好情況 | 最壞情況 | 空間 | 穩定性 |
|---|---|---|---|---|---|
| 選擇排序 | \(O(n^2)\) | \(O(n^2)\) | \(O(n^2)\) | \(O(1)\) | 不穩定 |
| 冒泡排序 | \(O(n^2)\) | \(O(n)\) | \(O(n^2)\) | \(O(1)\) | 穩定 |
| 插入排序 | \(O(n^2)\) | \(O(n)\) | \(O(n^2)\) | \(O(n)\) | 穩定 |
| 計數排序 | \(O(n + w)^1\) | \(O(n + w)\) | \(O(n + w)\) | \(O(n + w)\) | 穩定 |
| 基數排序 | \(O(kn + \sum\limits_{i = 1}^{k} w_i)^2\) | \(O(kn + \sum\limits_{i = 1}^{k} w_i)\) | \(O(kn + \sum\limits_{i = 1}^{k} w_i)\) | \(O(n + k)\) | 穩定 |
| 快速排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n^2)\) | \(O(\log n) \sim O(n)\) | 不穩定 |
| 歸併排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n)\) | 穩定 |
| 堆排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n \log n)\) | \(O(1)\) | 不穩定 |
| 桶排序 | \(O(n + \frac{n^2}{k} + k)^3\) | \(O(n)\) | \(O(n^2)\) | \(O(n + m)^4\) | 穩定 |
| 希爾排序 | \(O(n \log n) \sim O(n^2)\) | \(O(n^{1.3})\) | \(O(n^2)\) | \(O(1)\) | 不穩定 |
| 錦標賽排序 | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n \log n)\) | \(O(n)\) | 穩定 |
| \(\text{tim}\) 排序 | \(O(n \log n)\) | \(O(n)\) | \(O(n \log n)\) | \(O(n)\) | 穩定 |
\(^1\):其中 \(w\) 為排序元素的值域。
\(^2\):其中 \(k\) 為排序元素的最大位數,\(w_i\) 為第 \(i\) 個關鍵字的值域。
\(^3\):其中 \(k\) 表示將 \(n\) 個元素放進 \(m\) 個桶中,每個桶的數據為 \(k = \frac{n}{m}\)。
\(^4\):其中 \(m\) 表示將 \(n\) 個元素放進的 \(m\) 個桶。
首碼和
定義
首碼和可以簡單理解為「數列的前 \(\text{i}\) 項的和」,是一種重要的預處理方式,能大大降低查詢的時間複雜度。
一維首碼和
預處理遞推式為:
\[p_i = p_{i - 1} + a_i \]查詢 \([l, r]\) 的數值:
\[ans = p_r - p_{l - 1} \]二維首碼和
預處理遞推式為:
\[p_{i, j} = p_{i - 1, j} + p_{i, j - 1} - p_{i - 1, j - 1} + a_{i, j} \]查詢 \((i, j) \sim (k, w)\) 的數值:
\[ans = p_{k, w} - p_{k, j - 1} - p_{i - 1, w} + p_{i - 1, j - 1} \]樹上首碼和
設 \(s_i\) 表示結點 \(i\) 到根節點的權值總和。
若是點權,\(x, y\) 路徑上的和為 \(s_x + s_y - s_{lca} - s_{fa_{lca}}\)
若是邊權,\(x, y\) 路徑上的和為 \(s_x + s_y - 2 \times s_{lca}\)
差分
定義
差分是一種和首碼和相對的策略,可以當作是求和的逆運算。
這種策略的定義是令 \(b_i = \begin{cases} a_i - a_{i - 1} \, &i \in[2, n] \\ a_1 \, &i = 1 \end{cases}\)
性質
-
\(a_i\) 的值是 \(b_i\) 的首碼和,即 \(a_n = \sum\limits_{i = 1}^n b_i\)。
-
計算 \(a_i\) 的首碼和 \(sum = \sum\limits_{i = 1}^n a_i = \sum\limits_{i = 1}^n \sum\limits_{j = 1}^{i} b_j = \sum\limits_{i = 1}^n (n - i + 1) b_i\)。
它可以維護多次對序列的一個區間加上一個數,併在最後詢問某一位的數或是多次詢問某一位的數。註意修改操作一定要在查詢操作之前。
樹上差分
樹上差分可以理解為對樹上的某一段路徑進行差分操作,這裡的路徑可以類比一維數組的區間進行理解。例如在對樹上的一些路徑進行頻繁操作,並且詢問某條邊或者某個點在經過操作後的值的時候,就可以運用樹上差分思想了。
樹上差分通常會結合樹基礎和最近公共祖先來進行考察。樹上差分又分為點差分與邊差分,在實現上會稍有不同。
點差分
舉例:對樹上的一些路徑 \(\delta(s_1, t_1), \delta(s_2, t_2), \delta(s_3, t_3)\dots\) 進行訪問,問一條路徑 \(\delta(s, t)\) 上的點被訪問的次數。
對於一次 \(\delta(s, t)\) 的訪問,需要找到 \(s\) 與 \(t\) 的公共祖先,然後對這條路徑上的點進行訪問(點的權值加一),若採用 \(\text{DFS}\) 演算法對每個點進行訪問,由於有太多的路徑需要訪問,時間上承受不了。這裡進行差分操作:
\[\begin{aligned} &d_s\leftarrow d_s + 1\\ &d_{lca}\leftarrow d_{\textit{lca}} - 1\\ &d_t\leftarrow d_t + 1\\ &d_{f(\textit{lca})}\leftarrow d_{f(\textit{lca})} - 1\\ \end{aligned} \]其中 \(f(x)\) 表示 \(x\) 的父親節點,\(d_i\) 為點權 \(a_i\) 的差分數組。
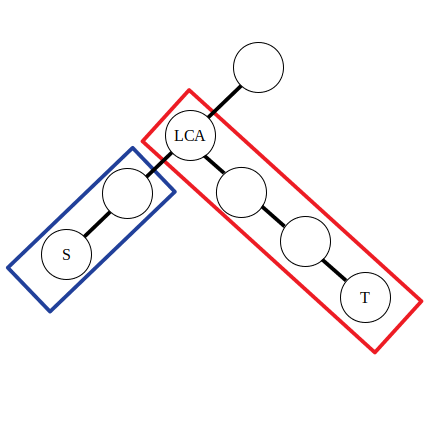
可以認為公式中的前兩條是對藍色方框內的路徑進行操作,後兩條是對紅色方框內的路徑進行操作。不妨令 \(\textit{lca}\) 左側的直系子節點為 \(\textit{left}\)。那麼有 \(d_{\textit{lca}} - 1 = a_{\textit{lca}} - (a_{\textit{left}} + 1)\),\(d_{f(\textit{lca})} - 1 = a_{f(\textit{lca})} - (a_{\textit{lca}} + 1)\)。可以發現實際上點差分的操作和上文一維數組的差分操作是類似的。
邊差分
若是對路徑中的邊進行訪問,就需要採用邊差分策略了,使用以下公式:
\[\begin{aligned} &d_s\leftarrow d_s + 1\\ &d_t\leftarrow d_t + 1\\ &d_{\textit{lca}}\leftarrow d_{\textit{lca}} - 2\\ \end{aligned} \]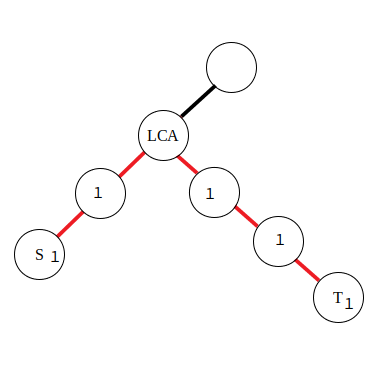
由於在邊上直接進行差分比較困難,所以將本來應當累加到紅色邊上的值向下移動到附近的點里,那麼操作起來也就方便了。對於公式,有了點差分的理解基礎後也不難推導,同樣是對兩段區間進行差分。




