• 第三講：深入淺出的索引上：
  • 引入：
  • 索引的常見模型：
    • • 哈希表：
      • 結論：
  • 有序數組：
    • • 弊端：
  • 二叉搜索樹
    • • 特點：
      • 例子：
      • 思考：為什麼資料庫存儲使用b+樹 而不是二叉樹
  • “N 叉”樹
    • • 例子：
  • 筆鋒一轉
  • InnoDB 的索引模型
  • 索引維護
  • 基於上面的索引維護過程說明，我們來討論一個案例：
  • 小結：
  • 補充：
  • 問題：

第三講：深入淺出的索引上：

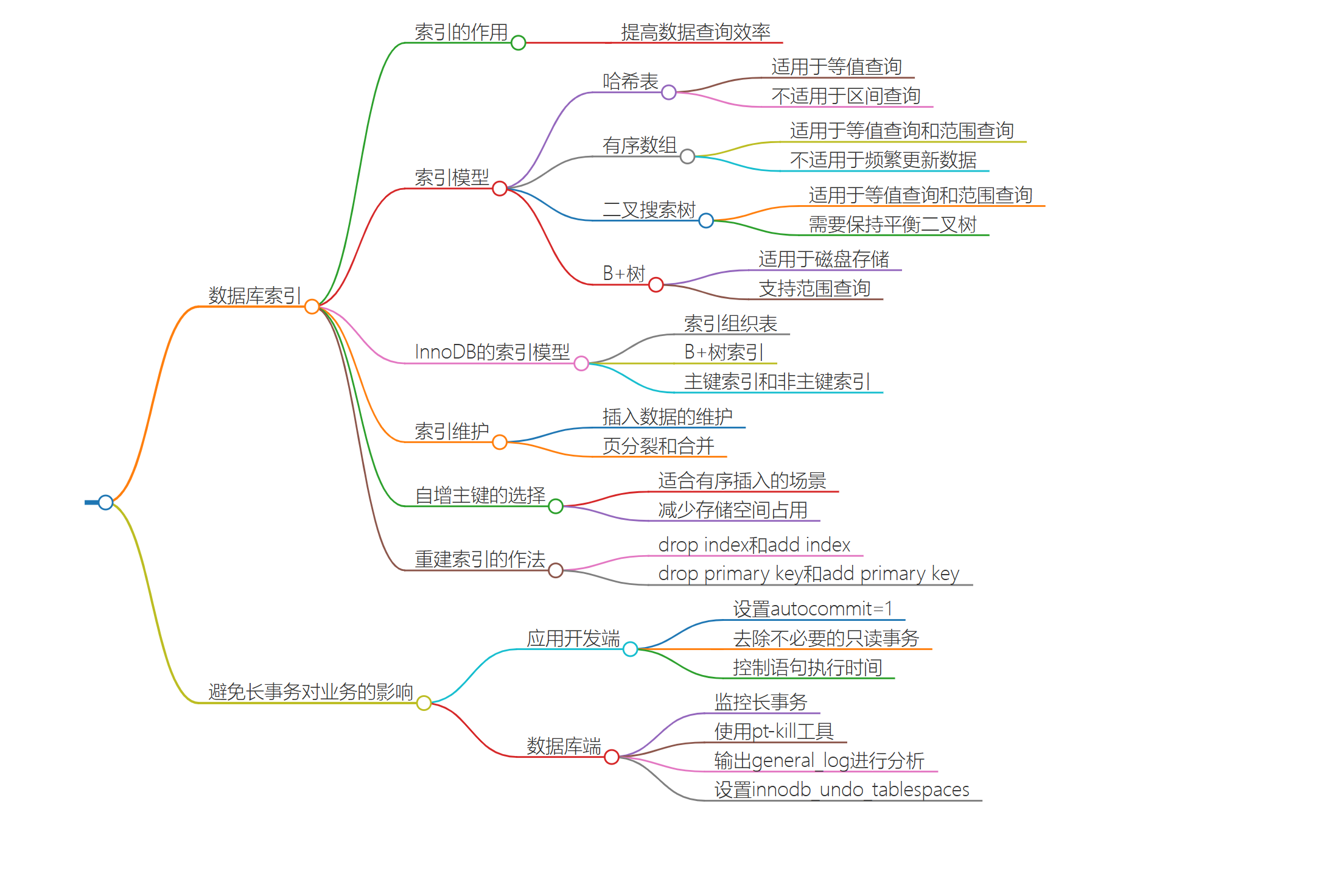
引入：

​ 提到資料庫索引，我想你並不陌生，在日常工作中會經常接觸到。比如某一個 SQL 查詢比較慢，分析完原因之後，你可能就會說“給某個欄位加個索引吧”之類的解決方案。但到底什麼是索引，索引又是如何工作的呢？今天就讓我們一起來聊聊這個話題吧。

​ 資料庫索引的內容比較多，我分成了上下兩篇文章。索引是資料庫系統裡面最重要的概念之一，所以我希望你能夠耐心看完。在後面的實戰文章中，我也會經常引用這兩篇文章中提到的知識點，加深你對資料庫索引的理解。

​ 一句話簡單來說，索引的出現其實就是為了提高數據查詢的效率，就像書的目錄一樣。一本 500 頁的書，如果你想快速找到其中的某一個知識點，在不藉助目錄的情況下，那我估計你可得找一會兒。同樣，對於資料庫的表而言，索引其實就是它的“目錄”。

索引的常見模型：

​ 索引的出現是為了提高查詢效率，但是實現索引的方式卻有很多種，所以這裡也就引入了索引模型的概念。可以用於提高讀寫效率的數據結構很多，這裡我先給你介紹三種常見、也比較簡單的數據結構，它們分別是哈希表、有序數組和搜索樹。

哈希表：

​ 哈希表是一種以鍵 - 值（key-value）存儲數據的結構，我們只要輸入待查找的鍵即 key，就可以找到其對應的值即 Value。哈希的思路很簡單，把值放在數組裡，用一個哈希函數把 key 換算成一個確定的位置，然後把 value 放在數組的這個位置。

​ 不可避免地，多個 key 值經過哈希函數的換算，會出現同一個值的情況。處理這種情況的一種方法是，拉出一個鏈表。

​ 假設，你現在維護著一個身份證信息和姓名的表，需要根據身份證號查找對應的名字，這時對應的哈希索引的示意圖如下所示：

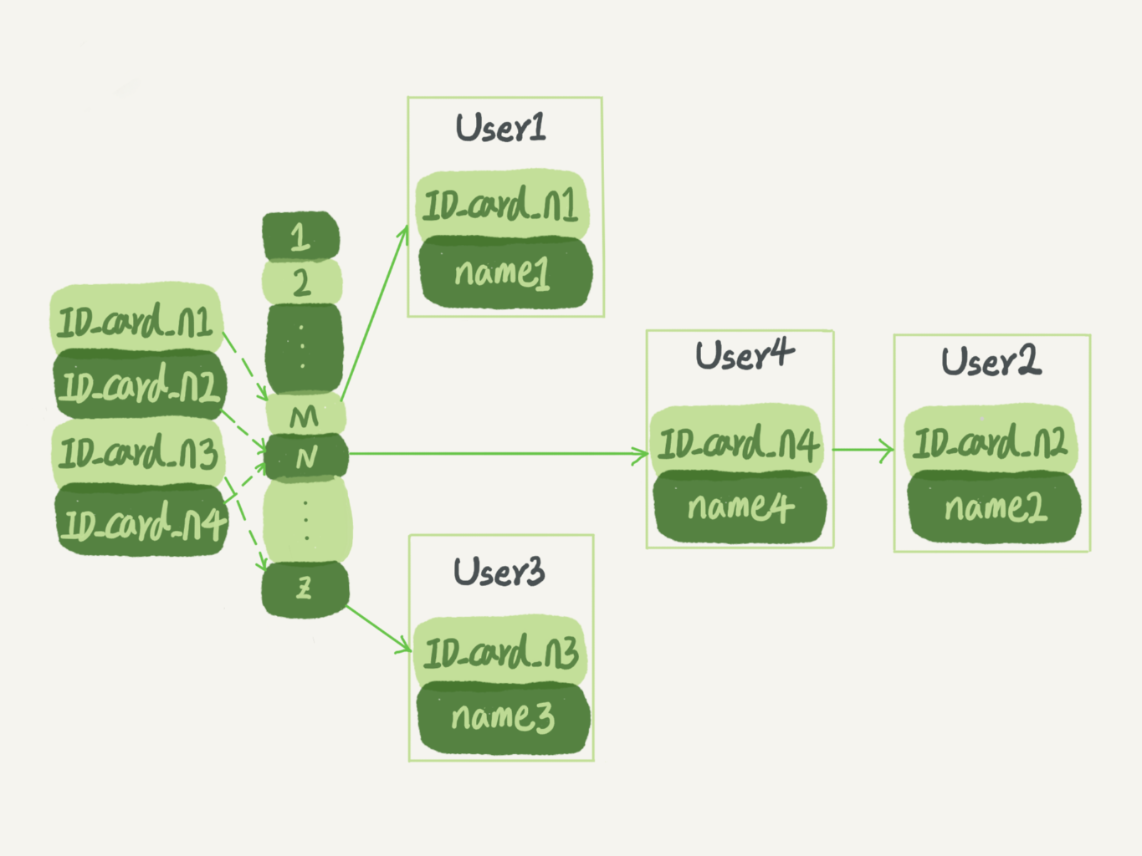
​ 圖中，User2 和 User4 根據身份證號算出來的值都是 N，但沒關係，後面還跟了一個鏈表。假設，這時候你要查 ID_card_n2 對應的名字是什麼，處理步驟就是：首先，將 ID_card_n2 通過哈希函數算出 N；然後，按順序遍歷，找到 User2。

​ 需要註意的是，圖中四個 ID_card_n 的值並不是遞增的，這樣做的好處是增加新的 User 時速度會很快，只需要往後追加。但缺點是，因為不是有序的，所以哈希索引做區間查詢的速度是很慢的。

​ 你可以設想下，如果你現在要找身份證號在[ID_card_X, ID_card_Y]這個區間的所有用戶，就必須全部掃描一遍了。

結論：

​ 哈希表只適用於等值查詢，其區間查詢效率很低，比如 Memcached 及其他一些 NoSQL 引擎。

（批註：等值查詢就是用等號來匹配查詢結果，分為單條件查詢、多條件查詢，與等值查詢對應的是模糊查詢、範圍查詢）

​

有序數組：

​ 而有序數組在等值查詢和範圍查詢場景中的性能就都非常優秀。還是上面這個根據身份證號查名字的例子，如果我們使用有序數組來實現的話，示意圖如下所示：

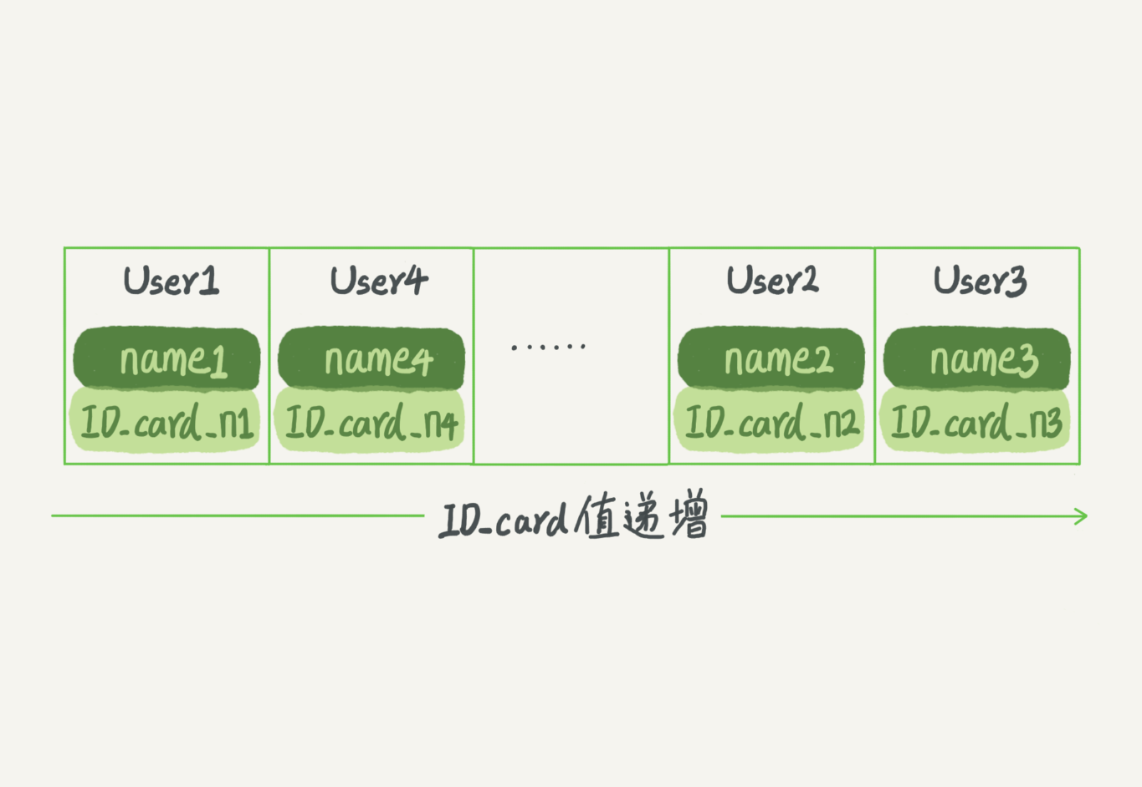
​ 這裡我們假設身份證號沒有重覆，這個數組就是按照身份證號遞增的順序保存的。這時候如果你要查 ID_card_n2 對應的名字，用二分法就可以快速得到，這個時間複雜度是 O(log(N))。

​ 同時很顯然，這個索引結構支持範圍查詢。你要查身份證號在[ID_card_X, ID_card_Y]區間的 User，可以先用二分法找到 ID_card_X（如果不存在 ID_card_X，就找到大於 ID_card_X 的第一個 User），然後向右遍歷，直到查到第一個大於 ID_card_Y 的身份證號，退出迴圈。

弊端：

​ 如果僅僅看查詢效率，有序數組就是最好的數據結構了。但是，在需要更新數據的時候就麻煩了，你往中間插入一個記錄就必須得挪動後面所有的記錄，成本太高。

​ 所以，有序數組索引只適用於靜態存儲引擎，比如你要保存的是 2017 年某個城市的所有人口信息，這類不會再修改的數據。

二叉搜索樹

​ 二叉搜索樹也是課本里的經典數據結構了。還是上面根據身份證號查名字的例子，如果我們用二叉搜索樹來實現的話，示意圖如下所示：

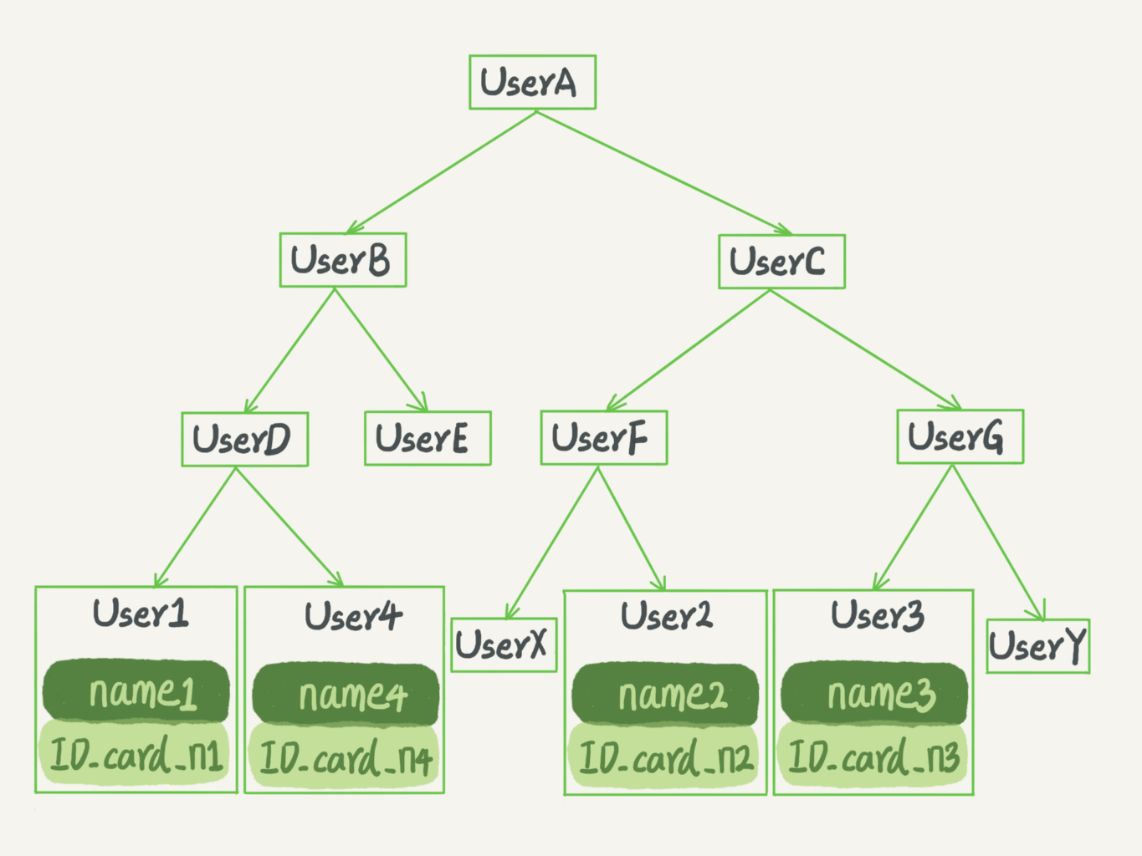
特點：

​ 二叉搜索樹的特點是：父節點左子樹所有結點的值小於父節點的值，右子樹所有結點的值大於父節點的值。這樣如果你要查 ID_card_n2 的話，按照圖中的搜索順序就是按照 UserA -> UserC -> UserF -> User2 這個路徑得到。這個時間複雜度是 O(log(N))。

​ 當然為了維持 O(log(N)) 的查詢複雜度，你就需要保持這棵樹是平衡二叉樹。為了做這個保證，更新的時間複雜度也是 O(log(N))。

​ 樹可以有二叉，也可以有多叉。多叉樹就是每個節點有多個兒子，兒子之間的大小保證從左到右遞增。二叉樹是搜索效率最高的，但是實際上大多數的資料庫存儲卻並不使用二叉樹。其原因是，索引不止存在記憶體中，還要寫到磁碟上。

例子：

​ 你可以想象一下一棵 100 萬節點的平衡二叉樹，樹高 20。一次查詢可能需要訪問 20 個數據塊。在機械硬碟時代，從磁碟隨機讀一個數據塊需要 10 ms 左右的定址時間。也就是說，對於一個 100 萬行的表，如果使用二叉樹來存儲，單獨訪問一個行可能需要 20 個 10 ms 的時間，這個查詢可真夠慢的。

思考：為什麼資料庫存儲使用b+樹 而不是二叉樹

​ 答：因為二叉樹樹高過高，每次查詢都需要訪問過多節點，即訪問數據塊過多，而從磁碟隨機讀取數據塊過於耗時。

“N 叉”樹

​ 為了讓一個查詢儘量少地讀磁碟，就必須讓查詢過程訪問儘量少的數據塊。那麼，我們就不應該使用二叉樹，而是要使用“N 叉”樹。這裡，“N 叉”樹中的“N”取決於數據塊的大小。

例子：

​ 以 InnoDB 的一個整數欄位索引為例，這個 N 差不多是 1200。這棵樹高是 4 的時候，就可以存 1200 的 3 次方個值，這已經 17 億了。考慮到樹根的數據塊總是在記憶體中的，一個 10 億行的表上一個整數欄位的索引，查找一個值最多只需要訪問 3 次磁碟。其實，樹的第二層也有很大概率在記憶體中，那麼訪問磁碟的平均次數就更少了。

​ N 叉樹由於在讀寫上的性能優點，以及適配磁碟的訪問模式，已經被廣泛應用在資料庫引擎中了。

​ 不管是哈希還是有序數組，或者 N 叉樹，它們都是不斷迭代、不斷優化的產物或者解決方案。資料庫技術發展到今天，跳錶、LSM 樹等數據結構也被用於引擎設計中，這裡我就不再一一展開了。

筆鋒一轉

​ 你心裡要有個概念，資料庫底層存儲的核心就是基於這些數據模型的。每碰到一個新資料庫，我們需要先關註它的數據模型，這樣才能從理論上分析出這個資料庫的適用場景。

​ 截止到這裡，我用了半篇文章的篇幅和你介紹了不同的數據結構，以及它們的適用場景，你可能會覺得有些枯燥。但是，我建議你還是要多花一些時間來理解這部分內容，畢竟這是資料庫處理數據的核心概念之一，在分析問題的時候會經常用到。當你理解了索引的模型後，就會發現在分析問題的時候會有一個更清晰的視角，體會到引擎設計的精妙之處。

​ 現在，我們一起進入相對偏實戰的內容吧。在 MySQL 中，索引是在存儲引擎層實現的，所以並沒有統一的索引標準，即不同存儲引擎的索引的工作方式並不一樣。而即使多個存儲引擎支持同一種類型的索引，其底層的實現也可能不同。

​ 由於 InnoDB 存儲引擎在 MySQL 資料庫中使用最為廣泛，所以下麵我就以 InnoDB 為例，和你分析一下其中的索引模型。

InnoDB 的索引模型

​ 在 InnoDB 中，表都是根據主鍵順序以索引的形式存放的，這種存儲方式的表稱為索引組織表。又因為前面我們提到的，InnoDB 使用了 B+ 樹索引模型，所以數據都是存儲在 B+ 樹中的。

​ 每一個索引在 InnoDB 裡面對應一棵 B+ 樹。

​ 假設，我們有一個主鍵列為 ID 的表，表中有欄位 k，並且在 k 上有索引。這個表的建表語句是：

mysql> create table T(
id int primary key, 
k int not null, 
name varchar(16),
index (k))engine=InnoDB;

表中 R1~R5 的 (ID,k) 值分別為 (100,1)、(200,2)、(300,3)、(500,5) 和 (600,6)，兩棵樹的示例示意圖如下。

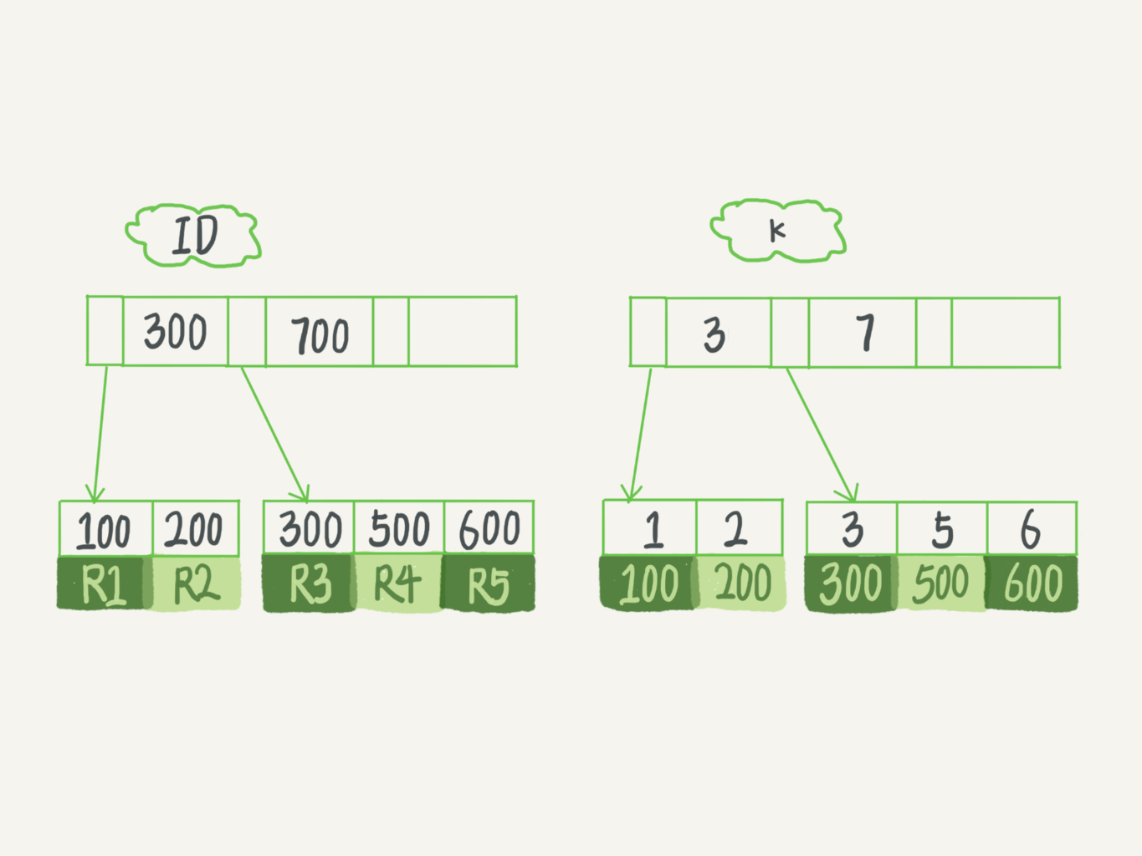
​ 從圖中不難看出，根據葉子節點的內容，索引類型分為主鍵索引和非主鍵索引。主鍵索引的葉子節點存的是整行數據。在 InnoDB 里，主鍵索引也被稱為聚簇索引（clustered index）。非主鍵索引的葉子節點內容是主鍵的值。在 InnoDB 里，非主鍵索引也被稱為二級索引（secondary index）。

​ 根據上面的索引結構說明，我們來討論一個問題：基於主鍵索引和普通索引的查詢有什麼區別？

• 如果語句是 select * from T where ID=500，即主鍵查詢方式，則只需要搜索 ID 這棵 B+ 樹；

• 如果語句是 select * from T where k=5，即普通索引查詢方式，則需要先搜索 k 索引樹，得到 ID 的值為 500，再到 ID 索引樹搜索一次。這個過程稱為回表。

​ 也就是說，基於非主鍵索引的查詢需要多掃描一棵索引樹。因此，我們在應用中應該儘量使用主鍵查詢。

索引維護

​ B+ 樹為了維護索引有序性，在插入新值的時候需要做必要的維護。以上面這個圖為例，如果插入新的行 ID 值為 700，則只需要在 R5 的記錄後面插入一個新記錄。如果新插入的 ID 值為 400，就相對麻煩了，需要邏輯上挪動後面的數據，空出位置。

​ 而更糟的情況是，如果 R5 所在的數據頁已經滿了，根據 B+ 樹的演算法，這時候需要申請一個新的數據頁，然後挪動部分數據過去。這個過程稱為頁分裂。在這種情況下，性能自然會受影響。

​ 除了性能外，頁分裂操作還影響數據頁的利用率。原本放在一個頁的數據，現在分到兩個頁中，整體空間利用率降低大約 50%。

​ 當然有分裂就有合併。當相鄰兩個頁由於刪除了數據，利用率很低之後，會將數據頁做合併。合併的過程，可以認為是分裂過程的逆過程。

基於上面的索引維護過程說明，我們來討論一個案例：

​ 你可能在一些建表規範裡面見到過類似的描述，要求建表語句里一定要有自增主鍵。當然事無絕對，我們來分析一下哪些場景下應該使用自增主鍵，而哪些場景下不應該。(強制要求一個自增主鍵不會出大問題，且適用絕大多數場景。因此會定下這樣的規範。)

​ 自增主鍵是指自增列上定義的主鍵，在建表語句中一般是這麼定義的:

NOT NULL PRIMARY KEY AUTO_INCREMENT

​ 插入新記錄的時候可以不指定 ID 的值，系統會獲取當前 ID 最大值加 1 作為下一條記錄的 ID 值。也就是說，自增主鍵的插入數據模式，正符合了我們前面提到的遞增插入的場景。每次插入一條新記錄，都是追加操作，都不涉及到挪動其他記錄，也不會觸發葉子節點的分裂。而有業務邏輯的欄位做主鍵，則往往不容易保證有序插入，這樣寫數據成本相對較高。

​ 除了考慮性能外，我們還可以從存儲空間的角度來看。假設你的表中確實有一個唯一欄位，比如字元串類型的身份證號，那應該用身份證號做主鍵，還是用自增欄位做主鍵呢？

​ 由於每個非主鍵索引的葉子節點上都是主鍵的值。如果用身份證號做主鍵，那麼每個二級索引的葉子節點占用約 20 個位元組，而如果用整型做主鍵，則只要 4 個位元組，如果是長整型（bigint）則是 8 個位元組。

​ 顯然，主鍵長度越小，普通索引的葉子節點就越小，普通索引占用的空間也就越小。

​ 所以，從性能和存儲空間方面考量，自增主鍵往往是更合理的選擇。

​ 有沒有什麼場景適合用業務欄位直接做主鍵的呢？還是有的。比如，有些業務的場景需求是這樣的：

• 只有一個索引；

• 該索引必須是唯一索引。

你一定看出來了，這就是典型的 KV 場景。由於沒有其他索引，所以也就不用考慮其他索引的葉子節點大小的問題。這時候我們就要優先考慮上一段提到的“儘量使用主鍵查詢”原則，直接將這個索引設置為主鍵，可以避免每次查詢需要搜索兩棵樹。

（批註：key value場景就是存在業務唯一欄位列，然後整行數據相當於value）

小結：

​ 今天，我跟你分析了資料庫引擎可用的數據結構，介紹了 InnoDB 採用的 B+ 樹結構，以及為什麼 InnoDB 要這麼選擇。B+ 樹能夠很好地配合磁碟的讀寫特性，減少單次查詢的磁碟訪問次數。

​ 由於 InnoDB 是索引組織表，一般情況下我會建議你創建一個自增主鍵，這樣非主鍵索引占用的空間最小。但事無絕對，我也跟你討論了使用業務邏輯欄位做主鍵的應用場景。

補充：

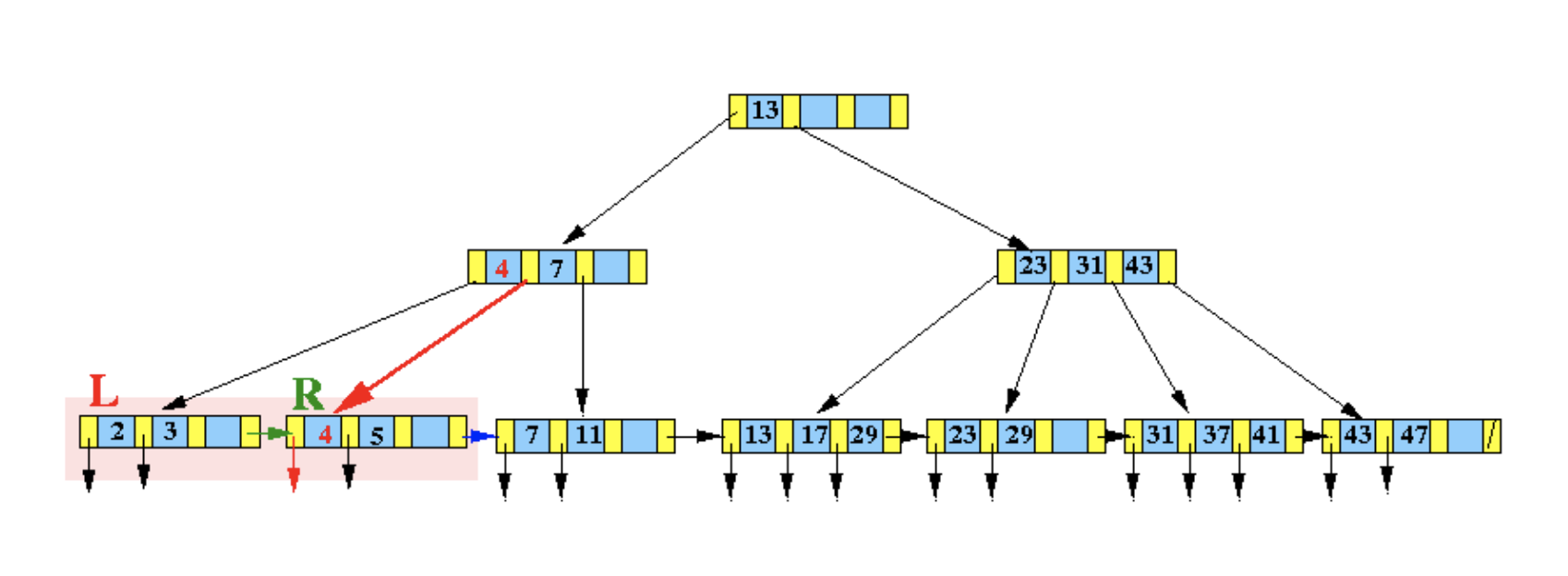
數據溢出，葉子結點分裂：

由於所在節點[2,3,5] 在插入之後數據溢出，因此需要分裂為兩個新的節點，同時調整父節點的索引數據：

問題：

​ 最後，我給你留下一個問題吧。對於上面例子中的 InnoDB 表 T，如果你要重建索引 k，你的兩個 SQL 語句可以這麼寫：

alter table T drop index k;
alter table T add index(k);

​ 如果你要重建主鍵索引，也可以這麼寫：

alter table T drop primary key;
alter table T add primary key(id);

我的問題是，對於上面這兩個重建索引的作法，說出你的理解。如果有不合適的，為什麼，更好的方法是什麼？

​ 重建索引 k 的做法是合理的，可以達到省空間的目的。但是，重建主鍵的過程不合理。不論是刪除主鍵還是創建主鍵，都會將整個表重建。所以連著執行這兩個語句的話，第一個語句就白做了。這兩個語句，你可以用這個語句代替 ： alter table T engine=InnoDB。在專欄的第 12 篇文章《為什麼表數據刪掉一半，表文件大小不變？》中，我會和你分析這條語句的執行流程。