LeetCode46全排列(回溯入門)

歡迎訪問我的GitHub

這裡分類和彙總了欣宸的全部原創(含配套源碼)：https://github.com/zq2599/blog_demos

題目描述

• 難度：中等

• 給定一個不含重覆數字的數組 nums ，返回其 所有可能的全排列 。你可以 按任意順序 返回答案

• 示例 1

輸入：nums = [1,2,3]
輸出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

• 示例 2

輸入：nums = [0,1]
輸出：[[0,1],[1,0]]

• 示例 3

輸入：nums = [1]
輸出：[[1]]

個人回溯和46題的理解

• 在很多刷題文章和書籍中，此題都被用做回溯演算法的第一題，可見該題很有代表性，搞定此題意味著對回溯有了最基本的瞭解，當然就個人感受而言，以此作為回溯的第一題弊端也不小：本以為掌握了基本套路，刷其他回溯題的時候套上去即可，結果後來發下一道題都套不成功...

• 套不成功？是因為此題沒有代表性嗎？當然不是，這是道典型的回溯演算法題，但個人的感覺是：解題的關鍵不是套用模板，而是對回溯思想的理解，我個人的理解是：深度至上

• 所謂深度至上，就是弄清楚在當前深度能做什麼，例如46題全排列，一個深度意味著可選數字中做了一輪選擇，每選中一個，都牢牢占據這一層的固定位置，下麵的子樹都要有他

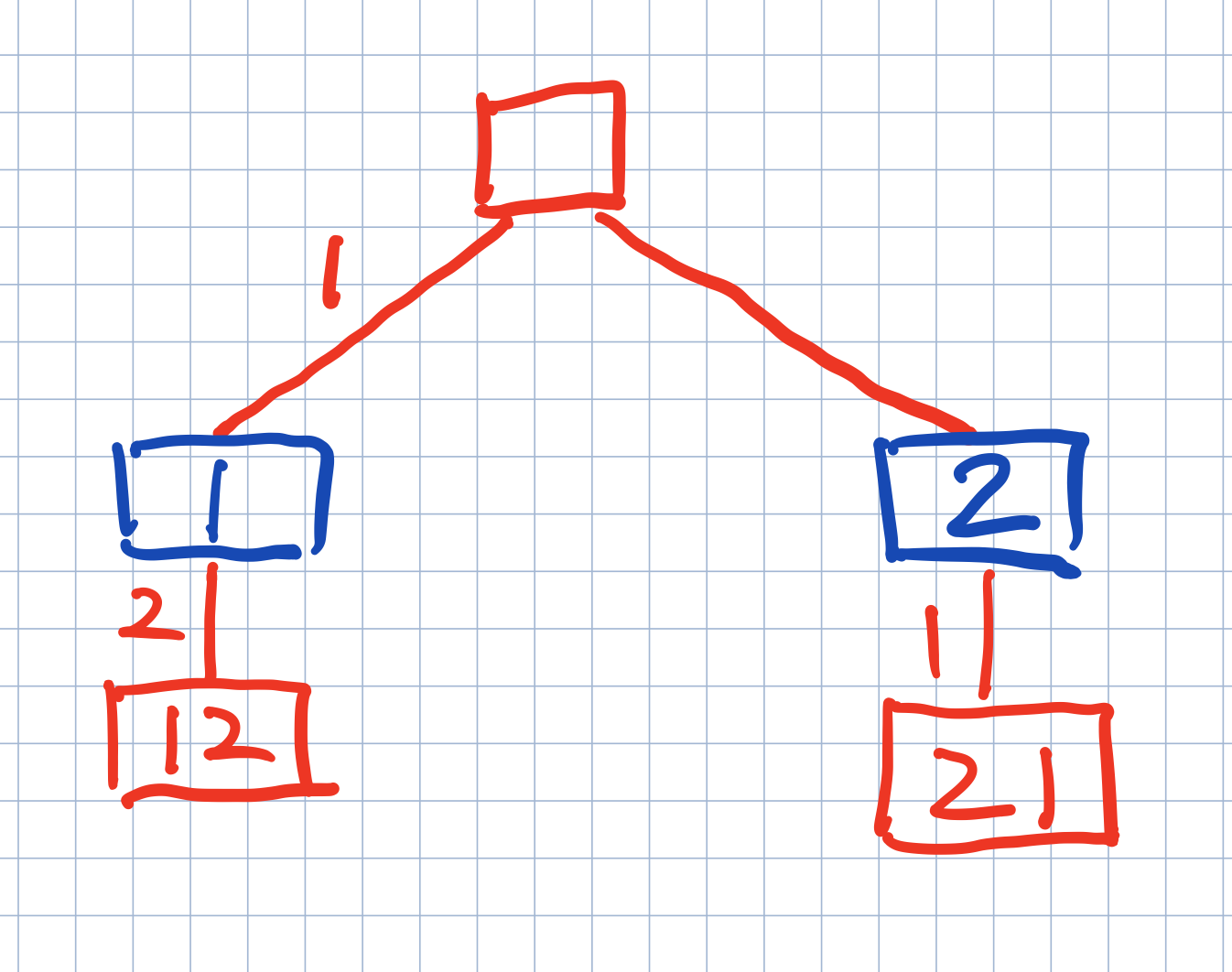
• 只要理解了深度至上，就清楚在當前做任何事情的時候都要確保深度固定，下圖是[1,2]兩個數字全排列的手繪圖，邊上數字表示選擇，方框中的數字表示選擇後的結果，請看藍色框，在選擇2的時候，要牢記當深度只能有一個數字，於是，剛纔選擇1的時候記錄存在路徑中的1就要果斷刪除，牢記當前層應該占據哪個位置，回溯的效果就有了

解題思路

• 要用回溯演算法解此題，有幾個關鍵要註意

• 全排列，意味著相同數字只要排列不同，也能算作結果的一種

• 雖然不推薦用模板去套，但回溯該有的幾個核心概念還是不能少的：

1. 終止條件：只要組合的數字達到給定數字的長度，就可以終止了

2. 路徑：就是正在組合的元素，可以用數組表達

• 此外還要有個輔助參數，用於記錄那些值不能參與組合，以上圖為例，在藍色那一層如果選擇了1，那麼在下一層就不能再選擇1了，所以在組合的時候，要有地方可以查到1不可用

編碼

• 接下來可以寫代碼了，如下，有幾處要註意的地方稍後會提到

public class L0046 {

    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> permute(int[] nums) {
        // 回溯過程中的重要輔助參數：標記nums數組中有哪些已經使用過
        boolean[] used = new boolean[nums.length];
        // 回溯過程中的重要輔助參數：路徑
        int[] path = new int[nums.length];

        dfs(nums, used, path, 0);
        return res;
    }

    public void dfs(int[] nums, boolean[] used, int[] path, int depth) {
        // 終止條件(深度達到)
        // 搜集：棧入res
        // 本題的終止條件是一次組合的長度達到數組長度
        if (depth==nums.length) {
            // 搜集結果
            // 千萬註意：這個path一直在使用中，所以不能把path放入res中，而是path的元素
//            res.add(Arrays.stream(path).boxed().collect(Collectors.toList()));


            List<Integer> list = new ArrayList<>();
            for(int val : path) {
                list.add(val);
            }

            res.add(list);
            return;
        }

        // for迴圈
        for (int i=0;i<nums.length;i++) {
            // 如果當前數字沒有用到，就標記，進入path，再做dfs
            if (!used[i]) {
                used[i] = true;
                // 註意，path的下標千萬不要用i！
                // 例如1和2的全排列，在製造[2,1]的時候，i=1，但此時要修改的是path[i]，
                // 所以path的下標應該是depth
                path[depth] = nums[i];
                // 一次遞歸，深度要加一
                dfs(nums, used, path, depth+1);
                used[i] = false;
            }
        }
    }

    public static void main(String[] args) {
        List<List<Integer>> list = new L0046().permute(new int[] {1,2,3});

        list.forEach(one -> {
           Tools.printOneLine(one);
        });

    }
}

• 上述代碼有以下幾處要註意

1. res用於搜集達到終止條件的記錄，也就是數字組合結果
2. dfs方法就是本次回溯操作的核心方法
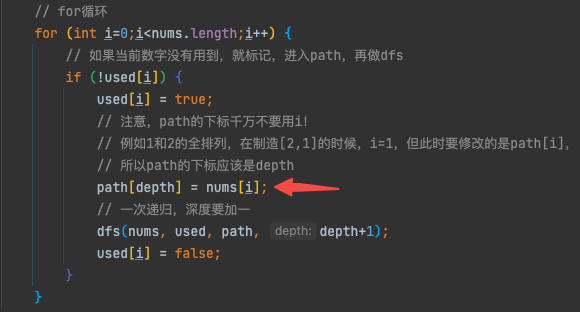
3. 下圖紅色箭頭所指代碼就是本題最重要的一行，可見for迴圈的執行過程中，修改的都是path數組的同一個位置的值，這就是剛纔提到的深度至上，只有進入了下麵的dfs方法後，深度變化，修改的path數組的位置才會發生變化

4. used數組用來記錄深度調用過程中，那些數字已經被使用了，當前不要再使用
5. 很多回溯的代碼中，用棧對象保持path中的數據，入棧push，出棧pop都是標準操作，但是本題中用char數組，再配合depth，就可以滿足需要了，這種原始類型的使用也會帶來更好的性能

執行結果

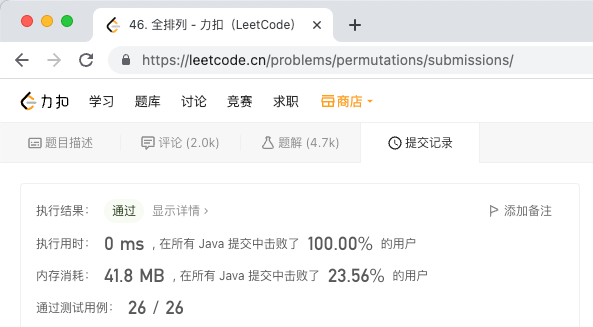
• 寫完代碼提交，執行結果如下，超過100.00%的提交

• 至此，回溯入門實戰已經完成，此時需要強烈提示：代碼中那個for迴圈，在每一層都遍歷nums的所有元素，那是此題的特殊操作，千萬不要以為是模板或者套路，其他回溯題中，不會像此題這樣每一層都遍歷的

歡迎關註博客園：程式員欣宸

學習路上，你不孤單，欣宸原創一路相伴...