一、緒論

1.1 基本概念

1. 加速比：表示加速效果。單個處理器運行花費時間 / P個處理器運行花費時間；\(S=\frac{T(1)}{T(p)}\)
2. 效率：\(E = \frac{S}{p} = \frac{T(1)}{T(p)\times p}\)
3. 開銷：\(C=T(p)\times p\)
4. 可擴展性：處理器數目增多時並行程式的行為；
5. 計算通信比：計算花費時間 / 處理器消息通信花費時間；
6. 計算：在1個時間單位內，每個PE（處理單元）能完成2個數相加，併在本地記憶體保存計算結果；
7. 通信：在3個單位時間內，一個PE能夠把數據從自己的本地記憶體發送到另一個PE的本地記憶體；
8. 輸入和輸出：程式開始時，整個輸入數組A保存在0號處理單元PE0，程式結束時，計算結果應匯聚到PE0；
9. 同步：所有PE同時進行計算、通信，或處於閑置狀態；

1.2 求和案例

1.2.1 分配流程

PE = 1：即為串列。

PE = 2：PE#0分1半任務給PE#1，分別計算，PE#1將求和後數據匯聚到PE#0。

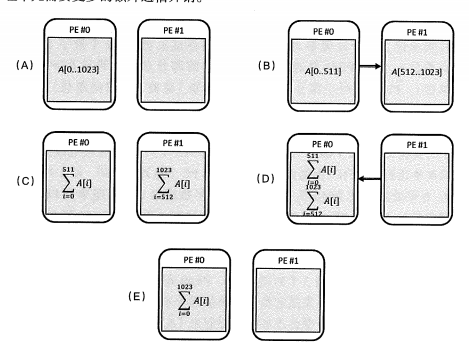
PE = 4：

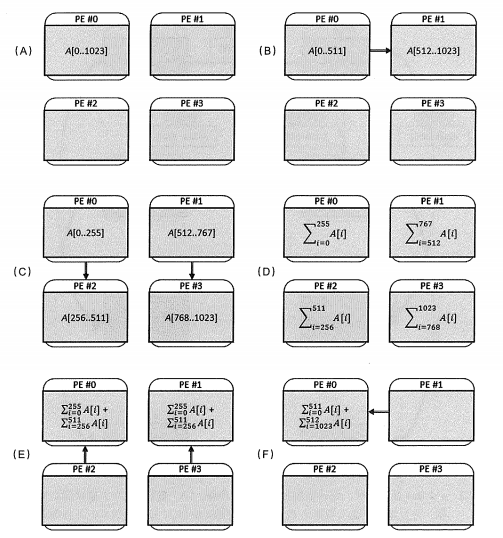
1.2.2 分發時間計算

以PE = 2為例

1. 最初PE#0存儲全部數據；
2. PE#0發送一般數據給PE#1，花費3個單位時間；（自己規定的，見1.2.4）
3. 每個處理單元將數據相加，花費511個單元時間；（因為每個處理器分別有511個數據）
4. PE#1求和後數據返回給PE#1，花費3個單元時間；
5. PE#0把2部分數據相加，花費1個時間單元；

共計 3 + 511 + 3 + 1 個時間單元

通用表達式

使用\(p=2^{q}\)個處理單元，以及\(n=2^{k}\)個輸入整數

• 數據分發次數：\(3 \times q\)
• 本地求和：\(\frac{n}{p} -1 = 2^{k-q}-1\)
• 收集中間數據：\(3 \times q\)
• 中間結果求和：：\(q\)

則共 \(T(p,n)=T(2^{q},2^{k})=3q+2^{k-q}-1+3q+q=2^{k-q}-1+7q\)

1.2.3 擴展性分析

強擴展性分析：改變處理器的數量，並行計算時間、加速比、開銷和效率變化規律；

弱擴展性分析：改變處理器的數量，同時改變數據量，並行計算時間、加速比、開銷和效率變化規律；

上述演算法不是強擴展性，是弱擴展性。

1.2.4 一般情形計算

$\alpha $：執行一次單獨的假髮操作需要的時長

$\beta $：傳輸一批整數需要的時長；

運行時間：\(T_{\alpha,\beta }(p,n)=T(2^{q},2^{k})=\beta q+\alpha(2^{k-q}-1)+\beta q+\alpha q=2\beta q +\alpha (2^{k-q}-1 + q)\)

加速比：$S_{\alpha ,\beta } (2^{q}, 2^{k})=\frac{T_{\alpha ,\beta }(2^{0}, 2^{k})}{T_{\alpha ,\beta }(2^{q}, 2^{k}) }=\frac{\alpha(2^{k}-1)}{2\beta q + \alpha(2^{k-q}-1+q)} $

通信比：\(\gamma=\frac{\alpha}{\beta}\)

求解最優單元：\(2^{q}={\frac{\gamma\ln2}{2+\gamma}}2^{k}\)

比如，對於\(\gamma=\frac{1}{3}，n=1024\)，加速比最大可求\(p=1000\)

當處理數據規模固定，並行效率和加速比依賴於計算單元個數和計算通信比；

1.3 並行計算基礎

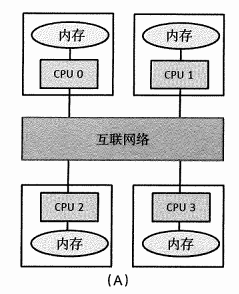
1.3.1 分散式記憶體

特點：每個PE只能訪問自己的本地記憶體，如果跨PE訪問，需要一個顯式的通信步驟。

數據劃分是分散式記憶體系統編程的關鍵。

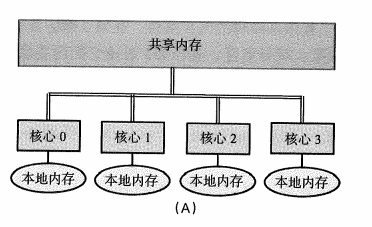
1.3.2 共用記憶體系統

通過一個共用匯流排或者縱橫交換機，所有的CPU都能訪問同一塊公共記憶體空間。

• 除了共用主存外，每個核心包含一塊更小的本地記憶體；
• 緩存一致性，存儲在本地緩存中的值和存儲在共用記憶體中的值保持一致；

1.4 並行程式設計考慮因素

1. 劃分：給定的問題劃分為子問題；
2. 通信：選定劃分方案決定了進程或縣城之間需要的通信量和通信類型；
3. 同步：為了以正確的方式共同運行，線程或進程之間可能需要同步操作；
4. 負載平衡：多個縣城或多個進程之間的工作量需要平均分配，以平衡他們各自的負載，並最小化空閑時間；

求和案例

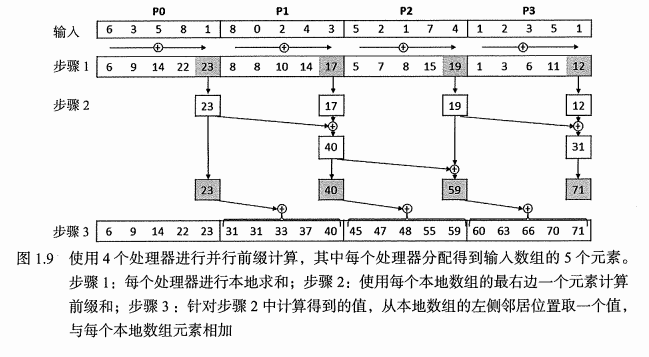
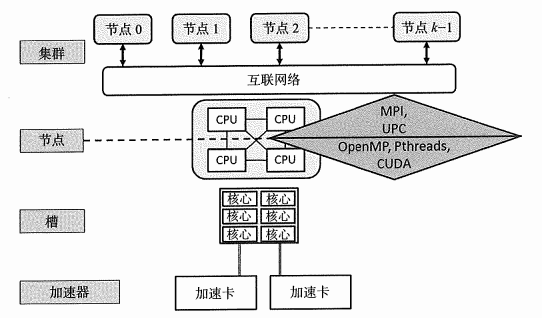
1.5 不同層次的並行

1. 節點級並行化：需要針對分散式記憶體機器的模型實現演算法，例如MPI(在第9章深入學習）或者UPC++(在第10章深人學習)等。
2. 節點內的並行化：通常基於針對共用記憶體系統(多核CPU)的語言，比如C++多線程(在第4章深人學習)，或者OpenMP(在第6章深人學習)。
3. 加速卡級的並行化：把一部分計算任務分配給加速卡承擔，比如大規模並行GPU等，藉助包括CVDA在內的特定語言(將在第7章深入學習)。

參考：《並行程式設計》