題目傳送門: >[【洛谷】P4710 [物理]平拋運動](https://www.luogu.com.cn/problem/P4710 "【洛谷】P4710 [物理]平拋運動") ## Step 1:前置芝士 您需要知道並瞭解以下芝士: 1. 數學: - 三角函數; 2. 物理: - 加速度公式; ...
題目傳送門:
Step 1:前置芝士
您需要知道並瞭解以下芝士:
- 數學:
- 三角函數;
- 物理:
- 加速度公式;
- 位移公式;
那麼如果您並不瞭解以上芝士,那麼請繼續向下看;如果您已經掌握以上芝士,那麼請跳至“Step 2”。
三角函數講解:
註意,本題為物理題解,故不會放出三角函數作圖過程、函數圖像、拓展公式、常考題型、易錯題型等,若需要請參考以下鏈接:
Bilibili: Link
WeChat: Link
如圖,三角形ABC為直角三角形,∠B為直角,∠A為θ。其中線段AB長為c,線段BC長為a,線段AC長為b。
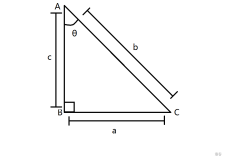
那麼對於直角三角形,它有六種三角函數:
- 正弦(sin)
- 餘弦(cos)
- 正切(tan)
- 餘切(cot)
- 正割(sec)
- 餘割(csc)
那他們都等於什麼呢:
\[\sin θ = \frac{對邊}{斜邊} = \frac{a}{b}; \]\[\cos θ = \frac{鄰邊}{斜邊} = \frac{c}{b}; \]\[\tan θ = \frac{對邊}{鄰邊} = \frac{a}{c}; \]\[\cot θ = \frac{鄰邊}{對邊} = \frac{c}{a}; \]\[\sec θ = \frac{斜邊}{鄰邊} = \frac{b}{c}; \]\[\csc θ = \frac{斜邊}{對邊} = \frac{b}{a}; \]好了,關於三角函數知道這麼多已經足夠我們做這道題了。
加速度公式:
\[a = \frac{(v_t - v_0)}{t}; \]其中,\(a\)為加速度;\(v_t\)為最終速度;\(v_0\)為初始速度;\(t\)為運動時間;
位移公式:
\[s = v_0 \times t + \frac{a \times t ^ 2}{2}; \]其中,\(a\)為加速度;\(v_0\)為初始速度;\(t\)為運動時間;\(s\)為位移;
Step 2:正文
先看題目:
一個可以視為質點的小球在點 \(A(x_0, y_0)\) 沿 \(x\) 軸負方向以某速度拋出,無視除重力外的所有阻力,最後恰好以速度 \(v\) 砸到 \(B(0, 0)\) 點。
易知,小球是在做平拋運動(看題目就知道了,那麼我們可以將平拋運動看做一個水平方向的勻速直線運動(只因無視所有阻力,則在水平方向不受力)和一個豎直方向的勻加速運動。在這個勻加速運動中,它的初速度為零,並且只受重力作用,所以是在做自由落體運動。
那麼,我們就把題目給出的速度分成兩個速度:水平方向的速度與豎直方向的速度。對於水平方向的速度,它是恆不變的,因為本題目無視所有阻力;而對於豎直方向的速度,它是在勻速增加的(重力加速度)。
看到題目是給的角度那麼我們就應該想到三角函數。就按題目中最後一個圖:
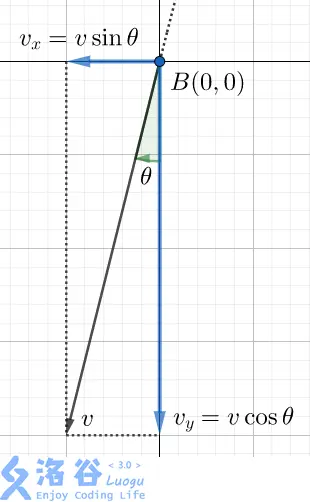
按上圖說,我們可以求出豎直方向的最終速度vy:
又有重力加速度的公式:
\[v = tg \]題目已經求出了豎直方向最終速度,那麼我們就可以用它求出時間,設重力加速度為g,則有:
醬紫我們就可以這麼表示時間t:
再由位移公式求出豎直方向的位移即縱坐標就好啦:
\[sy = v0(即為零) \times \frac{v \cos θ}{g} + \frac{g \times (\frac{v \cos θ}{g})^2}{2} \]分析完豎直方向,我們再看看水平方向。上面已經解釋過了水平方向是在做勻速直線運動,那最終的水平方向位移即橫坐標sx:
同時它也可以醬紫表示:
\[sx = vx \times \frac{v \cos θ}{g} \]我們再去分析水平方向的速度,繼續按介個圖說:

顯然良心出題人已經幫我們標出來了:
\[vx = v \sin θ \]那我們再將這個式子代入sx的式子中:
我們就又可以表示出橫坐標啦!下麵就是碼代碼就好啦。
Step 3:代碼
直接放代碼了就:
Link
#include <bits/stdc++.h>
using namespace std;
double sx,sy;
double vx,vy;
double v,d,g,t;
int main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>v;
cin>>d;
g=10.0;
t=v*cos(d)*1.0/g;
sy=(g*t*t)/2;
sx=v*sin(d);
sx*=t;
cout<<sx<<" "<<sy;
//fclose(stdin);
//fclose(stdout);
return 0;
}
建議不要在使用double類型時使用pow,就是TM這麼寫炸的。
就醬紫吧。
本文來自博客園,作者:Taunting_Wind,轉載請註明原文鏈接:https://www.cnblogs.com/xinao2186182144/p/17237773.html



