2023團隊天梯模擬賽 L2-3 智能護理中心統計 and L3-1 塔防游戲（23分)

来源:https://www.cnblogs.com/zdxxdz/archive/2023/04/19/17331874.html
-Advertisement-
Play Games

L2-3 智能護理中心統計 智能護理中心系統將轄下的護理點分屬若幹個大區，例如華東區、華北區等；每個大區又分若幹個省來進行管理；省又分市，等等。我們將所有這些有管理或護理功能的單位稱為“管理結點”。現在已知每位老人由唯一的一個管理結點負責，每個管理結點屬於唯一的上級管理結點管轄。你需要實現一個功能， ...


L2-3 智能護理中心統計

智能護理中心系統將轄下的護理點分屬若幹個大區，例如華東區、華北區等；每個大區又分若幹個省來進行管理；省又分市，等等。我們將所有這些有管理或護理功能的單位稱為“管理結點”。現在已知每位老人由唯一的一個管理結點負責，每個管理結點屬於唯一的上級管理結點管轄。你需要實現一個功能，來統計任何一個管理結點所負責照看的老人的數量。

註意這是一個動態問題，即隨時可能有老人加入某個管理結點，並且老人是有可能從一個管理結點換到另一個管理結點去的。

輸入格式：

輸入在第一行中給出 2 個正整數：N（≤104）是老人的總數量，即老人們從 1 到 N 編號；M（≤105）是歸屬關係的總數。

接下來是 M 行，每行給出一對歸屬關係，格式為：

A B

表示 A 歸屬於 B。A 或 B 如果是某個管理結點，則用不超過 4 個大寫英文字母表示其名稱；如果是某位老人，則用老人的編號表示。這裡每個 A 保證只有唯一的上級歸屬 B，且只有這個中心系統本身是沒有上級歸屬的。此外，輸入保證沒有老人自己承擔管理結點的角色，即 B 一定是一個管理結點，不可能是老人的編號。但一個管理結點既可以管轄下級結點，也可以直接護理一部分老人。

隨後每行給出一個指令，格式為：

指令 內容

如果 指令 為 T，則表示有老人要入院或轉院，內容 是某老人的編號和要去的管理結點的名稱，以空格分隔；如果 指令 為 Q，則 內容 是一個管理結點的名稱，意思是統計這個結點所負責照看的老人的數量；如果 指令 為 E，則表示輸入結束。題目保證指令總數不會超過 100 個。

輸出格式：

對每個 T 指令，將對應的老人轉存到對應的管理結點名下；對每個 Q 指令，在一行中輸出對應管理結點所負責照看的老人的數量。讀到 E 指令就結束程式。

輸入樣例：

10 23
EAST CNTR
ZJ EAST
SD EAST
WEST CNTR
SX WEST
HZ ZJ
JN SD
2 JN
8 JTH
6 XAHP
4 ZDYH
5 ZDYH
ZDYH HZ
HUZ ZJ
JX ZJ
1 JX
3 JN
WZ ZJ
XAHP XIAN
XIAN SX
YL SX
JTH XIAN
7 XAHP
Q EAST
T 1 YL
Q EAST
Q SX
T 8 ZDYH
Q HZ
Q HUZ
T 10 XAHP
Q CNTR
E

輸出樣例：

5
4
4
3
0
9

題解：老人為葉子節點，考慮到每次只有葉子節點的變化，所以只需要貪心計算葉子節點對對應的這條鏈的貢獻即可

//
#include<bits/stdc++.h>
using namespace std;
#define maxn 610938
int n,m;
int cnt1=0,cnt2=0,cnt=200000;
unordered_map<string,int>mapp;
int cot[maxn];
int yezi[maxn];
int pre[maxn];
int main()
{
    cin>>n>>m;
    string s1,s2;
    for(int i=1;i<=m;i++)
    {
        cin>>s1>>s2;
        if(s1[0]>='0'&&s1[0]<='9')
        {
            if(!mapp[s2])
            {
                ++cnt;
                mapp[s2]=cnt;
            }
            pre[stoi(s1)]=mapp[s2];
        }
        else
        {
            if(!mapp[s1])
            {
                ++cnt;
                mapp[s1]=cnt;
            }
            if(!mapp[s2])
            {
                ++cnt;
                mapp[s2]=cnt;
            }
            pre[mapp[s1]]=mapp[s2];
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(pre[i]!=0)
        {
            int x=pre[i];
            cot[i]=1;
            while(pre[x]!=x)
            {
                cot[x]++;
                x=pre[x];
            }
            cot[x]++;
        }
    }
    while(1)
    {
        char c;
        cin>>c;
        if(c=='E')
        {
            break;
        }
        if(c=='T')
        {
            int a;
            string b;
            cin>>a>>b;
            int x=pre[a];
            cot[a]=1;
            while(pre[x]!=x)
            {
                cot[x]--;
                x=pre[x];
            }
            cot[x]--;
            pre[a]=mapp[b];
            int y=pre[a];
            cot[a]=1;
            while(pre[y]!=y)
            {
                cot[y]++;
                y=pre[y];
            }
            cot[y]++;
        }
        if(c=='Q')
        {
            string x;
            cin>>x;
            cout<<cot[mapp[x]]<<endl;
        }
    }
}
View Code

 

 
--------------------
L3-1 塔防游戲

有一種簡單的塔防游戲是這樣的：給定一張由 n 行 m 列個方格子構成的地圖，玩家可以任選一個格子放置自己的大本營，還可以在任意一個格子里放置自己的防禦堡壘。大本營和每個防禦堡壘都有自己的防禦能力值 d，表示可以抵禦 d 個僵屍的攻擊。每一輪游戲開始時，玩家在規定時間內將本級別可以用的防禦堡壘佈置在地圖中，然後僵屍們就從地圖邊界涌入地圖中，向著大本營發起攻擊。每輪進攻持續一個固定的時長，結束後剩餘的僵屍就原地蒸發。

每隊僵屍可以向一個方格的上下左右四個方向移動。如果相鄰的目標方格沒有堡壘，它們就可以用 1 秒的時間移動過去，否則會被堡壘阻擋或者消滅。對每一隊僵屍（從同一地點出發的所有僵屍）而言，每秒會被堡壘消滅 1 個隊友，同時消耗掉該堡壘 1 個單位的防禦能力。當防禦能力降為 0，則該堡壘消失，剩下的僵屍則用 1 秒移動到這個方格繼續行進。註意：如果有多支僵屍隊都進入了同一個方格，它們並不會合併成一支隊伍。

所有的僵屍隊都會根據進攻開始時的地圖選擇被殲滅最少的到達大本營的路線，並且一直按照這個路線行進，中途不因為地圖狀態的改變而改變。當這樣的進攻路徑不唯一時，選擇能最快到達大本營的路徑。題目保證這樣的路徑所打掉的堡壘的佈局是唯一的。

本題就要求你計算出一輪攻擊結束時，地圖上的佈局情況。

輸入格式：

輸入首先在第一行中給出三個正整數：不超過 100 的 n 和 m，為地圖的尺寸；不超過 1000 的 T，為一輪攻擊持續的時長。

隨後給出 n+2 行，每行給出 m+2 個數字，每行中的數字都用空格分隔，表示攻擊開始前地圖上的佈局。其中第 1 行、第 1 列、第 n+2 行、第 m+2 列是地圖邊界外僵屍們出發的位置，這些位置上，0 表示沒有僵屍，其他正整數表示從該位置出發的僵屍們的數量。而地圖中的每個位置上，0 表示沒有堡壘，其它正整數表示該位置上堡壘的防禦能力值。大本營是一個特殊的建築，我們用一個負數 −D 表示這裡是大本營，其防禦能力值為 D。這裡的防禦值和任一隊僵屍的數量都不超過 100。

註意：僵屍不可在地圖邊界外移動，它們的第一個移動目標必須在地圖中，所以四個角落裡出現的僵屍可以被忽略，因為它們沒有進入地圖的途徑。

輸出格式：

輸出 n 行，每行 m 個數字，對應攻擊結束後地圖上每個方格的狀態。狀態的表示與輸入相同：沒有堡壘的地方輸出 0，有堡壘的地方輸出其剩餘防禦值，大本營的位置上輸出其剩餘防禦值的負值。

註意每行數字間以 1 個空格分隔，行首尾不得有多餘空格。

當大本營被攻陷時，游戲即刻結束。此時應輸出結束時的地圖狀態，並且在最後一行輸出一句 Game Over。

輸入樣例 1：

7 5 17
0 0 0 0 13 0 0
0 0 0 0 0 0 0
0 0 0 8 0 0 0
0 0 0 0 2 1 0
0 0 0 7 5 3 0
8 0 1 4 -10 1 0
0 0 0 3 3 0 0
0 0 8 0 9 0 0
0 0 0 4 0 0 0
 

輸出樣例 1：

0 0 0 0 0
0 0 8 0 0
0 0 0 2 0
0 0 7 5 0
0 0 0 -1 0
0 0 0 2 0
0 8 0 9 0
 

樣例說明：

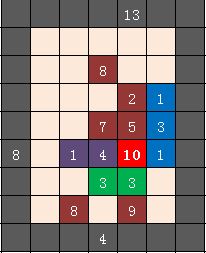
地圖佈局如下圖所示。

map.JPG

規模為 13 和 8 的兩隊僵屍都有兩種選擇，攻打藍色或者紫色堡壘都是消耗最少的。在這種情況下，規模為 13 的僵屍隊走藍色比較快，需要 1+1+1+2+4+2=11 秒到達大本營邊上；規模為 8 的僵屍隊走紫色比較快，需要 1+2+5=8 秒到達大本營邊上。

規模為 4 的僵屍隊比較慘，只能選擇綠色堡壘，最後被大本營邊上的綠色堡壘消滅。註意到在攻擊過程中，其實它們可以等到紫色堡壘被攻陷之後走紫色原始值為 4 的方格，但是因為路徑是在初始狀態下選定就不能改的，所以它們不能這樣選擇。

攻打大本營時，規模為 8 的僵屍隊剩下了 3 只先到達，在第 11 秒被大本營消滅。此時大本營還剩 7 個單位的防禦值，同時規模為 13 的僵屍隊剩下的 8 只進入了大本營相鄰的方格，開始攻擊。但此時距離本輪結束只剩 6 秒，結果大本營在結束時還剩 1 個單位的防禦值，玩家勝。

輸入樣例 2：

7 5 20
0 0 0 0 13 0 0
0 0 0 0 0 0 0
0 0 0 8 0 0 0
0 0 0 0 2 1 0
0 0 0 7 5 3 0
8 0 1 4 -10 1 0
0 0 0 3 3 0 0
0 0 8 0 9 0 0
0 0 0 4 0 0 0
 

輸出樣例 2：

0 0 0 0 0
0 0 8 0 0
0 0 0 2 0
0 0 7 5 0
0 0 0 0 0
0 0 0 2 0
0 8 0 9 0
Game Over
題解:
最開始以為是簡單的bfs，然後發現題目中有個很關鍵的點，所有的僵屍隊都會根據進攻開始時的地圖選擇被殲滅最少的到達大本營的路線，並且一直按照這個路線行進，
中途不因為地圖狀態的改變而改變。當這樣的進攻路徑不唯一時，選擇能最快到達大本營的路徑。題目保證這樣的路徑所打掉的堡壘的佈局是唯一的。

也就是說行經路線是一開始就定好的，所以不用寬搜。所以考慮spfa和dij的做法，由於這倆都是單源最短路，所以考慮反向從大本營開始跑spfa。 dis[i][0]代表破壞堡壘和移動的總消耗的最短路徑，
dis[i][1]代表僅破壞堡壘的總消耗的最短路徑。然後我們對於每個網格點，記錄是哪一個最小損失僵屍的點更新的他就行了。
最後按照這個路徑進行模擬就行。
大致思路就是這樣，但是天梯賽的數據真的好多坑。。。不想改了。。。
下麵附上一個23分的代碼
//
#include<bits/stdc++.h>
using namespace std;
#define maxn 610938
#define inf 1290311
int n,m,t;
struct no
{
    int x,y,nowtime,shu;
};
map<pair<int,int> ,pair<int,int>>mp;
int mapp[200][200];
queue<no>Q;
int dx[6]={1,-1,0,0};
int pre1[200];
int pre2[200];
int dy[6]={0,0,1,-1};
int mark[200][200];
int tx,ty;
int dis[200][200][2];
void bfs()
{
    dis[tx][ty][0]=0;
    dis[tx][ty][1]=0;
    memset(mark,0,sizeof(mark));
    queue<pair<int,int> >K;
    K.push(make_pair(tx,ty));
    while(K.size())
    {
        pair<int ,int> p1=K.front();
        K.pop();
        int x=p1.first;
        int y=p1.second;
        mark[x][y]=0;
        for(int i=0;i<4;i++)
        {
            if(x+dx[i]>=2&&y+dy[i]>=2&&x+dx[i]<=n+1&&y+dy[i]<=m+1)
            {
                
                if(x+dx[i]==tx&&y+dy[i]==ty)continue;
                if(dis[x+dx[i]][y+dy[i]][0]>dis[x][y][0]+1+mapp[x+dx[i]][y+dy[i]])
                {
                    dis[x+dx[i]][y+dy[i]][0]=dis[x][y][0]+1+mapp[x+dx[i]][y+dy[i]];
                    if(!mark[x+dx[i]][y+dy[i]])
                    {
                        mark[x+dx[i]][y+dy[i]]=1;
                        K.push(make_pair(x+dx[i],y+dy[i]));
                    }
                }
            }
        }
    }
    memset(mark,0,sizeof(mark));
    K.push(make_pair(tx,ty));
    while(K.size())
    {
        pair<int ,int> p1=K.front();
        K.pop();
        int x=p1.first;
        int y=p1.second;
        mark[x][y]=0;
        for(int i=0;i<4;i++)
        {
            if(x+dx[i]>=2&&y+dy[i]>=2&&x+dx[i]<=n+1&&y+dy[i]<=m+1)
            {
                if(x+dx[i]==tx&&y+dy[i]==ty)continue;
                if(dis[x+dx[i]][y+dy[i]][1]>dis[x][y][1]+mapp[x+dx[i]][y+dy[i]])
                {
                    dis[x+dx[i]][y+dy[i]][1]=dis[x][y][1]+mapp[x+dx[i]][y+dy[i]];
                    
                    mp[make_pair(x+dx[i],y+dy[i])]=make_pair(x,y);
                
                    if(!mark[x+dx[i]][y+dy[i]])
                    {
                        mark[x+dx[i]][y+dy[i]]=1;
                        K.push(make_pair(x+dx[i],y+dy[i]));
                    }
                }
                else
                {
                    if(dis[x+dx[i]][y+dy[i]][1]==dis[x][y][1]+mapp[x+dx[i]][y+dy[i]])
                    {
                        if(dis[x+dx[i]][y+dy[i]][0]<=dis[x][y][0]+1+mapp[x+dx[i]][y+dy[i]])continue;
                        
                        mp[make_pair(x+dx[i],y+dy[i])]=make_pair(x,y);
                        if(!mark[x+dx[i]][y+dy[i]])
                        {
                            mark[x+dx[i]][y+dy[i]]=1;
                            K.push(make_pair(x+dx[i],y+dy[i]));
                        }
                    }
                }
            }
        }
    }
}
int main()
{
    cin>>n>>m>>t;
    for(int i=1;i<=n+2;i++)
    for(int j=1;j<=m+2;j++)
    {
        {
            dis[i][j][0]=inf;
            dis[i][j][1]=inf;
        }
    
        cin>>mapp[i][j];
        if(i==1||i==n+2||j==1||j==m+2)
        {
            if(!mapp[i][j]) continue;
            if(i==1&&(j==1||j==m+2))continue;
            if(i==n+2&&(j==1||j==m+2))continue;
                for(int k=0;k<4;k++)
            {
                if(i+dx[k]>=2&&j+dy[k]>=2&&i+dx[k]<=n+1&&j+dy[k]<=m+1)
                {
                    Q.push(no{i+dx[k],j+dy[k],0,mapp[i][j]});
                }
            }
        }
        if(mapp[i][j]<0)
        {
            tx=i;
            ty=j;
        }
    }
    int fla=0;
    bfs();
    while(Q.size())
    {
        no tmp=Q.front();
        Q.pop();
        int x=tmp.x;
        int y=tmp.y;
        int pret=1+mapp[x][y];
        int num=tmp.shu;
        if(num>mapp[x][y])
        {
            num-=mapp[x][y];
            mapp[x][y]=0;
        }
        else
        {
            mapp[x][y]-=num;
            continue;
        }
    
        while(!(x==tx&&y==ty))
        {
            pair<int,int>R;
            R=mp[make_pair(x,y)];
            x=R.first;
            y=R.second;
            
             if(mapp[x][y])
            {
                if(x==tx&&y==ty)continue;
                pret=pret+1+mapp[x][y];
                if(num>mapp[x][y])
                {
                    num-=mapp[x][y];
                    mapp[x][y]=0;
                }
                else
                {
                    mapp[x][y]-=num;
                    break;
                }
            }
            else
            {
                if(x==tx&&y==ty)continue;
                pret++;
            }
        }
        if(x==tx&&y==ty)
        {
            int w=max(0,min(t-pret,num));
            mapp[tx][ty]+=w;
            mapp[tx][ty]=min(mapp[tx][ty],0);
            if(mapp[tx][ty]==0)
            {
                fla=1;
            }
        }
    }
    for(int i=2;i<=n+1;i++)
    for(int j=2;j<=m+1;j++)
    {
        if(j==2)
        cout<<mapp[i][j];
        else
        {
            cout<<" "<<mapp[i][j];
            if(j==m+1&&i!=n+1)
            cout<<endl;
        }
    }
    if(fla==1)
    {
        cout<<endl;
        cout<<"Game Over";
    }
}
View Code

 

 

您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 記錄-JavaScript常規加密技術
    這裡給大家分享我在網上總結出來的一些知識，希望對大家有所幫助 當今Web開發中，數據安全是一個至關重要的問題，為了確保數據的安全性，我們需要使用加密技術。JavaScript作為一種客戶端編程語言，可以很好地為數據進行加密。在本篇文章中，我們將為你提供一個常規JavaScript加密大全，以及案例代 ...
  • 比較幾種熱門Hybrid App前端框架
    在Vue3中，路由的基本配置是通過使用Vue Router庫來實現的。以下是Vue3中路由的基本配置步驟： 安裝Vue Router 使用npm或yarn在項目中安裝Vue Router： npm install vue-router // 或者 yarn add vue-router 創建路由實例 ...
  • vue全家桶進階之路33：Vue3 計算屬性computed
    在Vue3中，計算屬性可以使用computed函數來定義。 computed函數接受兩個參數：第一個參數是一個函數，該函數返回計算屬性的值；第二個參數是一個可選的配置對象，可以包含getter和setter函數，以及控制計算屬性緩存的緩存配置。 Vue3中的計算屬性與Vue2中的計算屬性相比有以下幾 ...
  • git merge 提示錯誤 fatal: refusing to merge unrelated histories
    拉去遠程分支代碼報錯：fatal: refusing to merge unrelated histories造成的原因是： 1、本地項目copy 其他項目的結構把.git 文件可拷貝過來了 且覆蓋了自己當前目錄的 .git 文件，然後將當前分支合遠程分支合併 因為兩個 .git 文件儲存庫的歷史數 ...
  • elementUI Table 表格編輯數據後停留當前位置
    後臺管理系統在實際開發中，表格如果在一定高度出現滾動條。 這時如果對錶格行數據進行編輯或者拖拽排序操作，數據刷新後滾動條會預設回到頂部，這樣體驗會不太好。 如果想保留在當前位置可以這樣操作： 1.el-table標簽添加ref屬性 <el-table :data="tableData" v-load ...
  • 05單件模式
    #經典的單件模式 public class Singleton { private static Singleton uniqueInstance; //一個靜態變數持有Singleton類的唯一實例。 // 其他有用的實例變數寫在這裡 //構造器聲明為私有，只有Singleton可以實例化這個類! ...
  • 【架構與設計】常見微服務分層架構的區別和落地實踐
    軟體工程的方方面面都遵循一個最基本的道理：沒有銀彈，架構分層模型更是如此，每一種都有各自優缺點，所以請根據不同的業務場景，並遵循簡單、可演進這兩個重要的架構原則選擇合適的架構分層模型即可。 ...
  • 3D輕量化引擎推出新技術，模型渲染更逼真！
    HOOPS Communicator在2021版本中，推出了基於PBR（Physically Based Rendering）的渲染特性以提供更高質量的渲染技術。 PBR將材料表示為一系列方程，這些方程對光如何從錶面反射進行建模，再通過GPU上運行的著色器代碼進行有效地實現。 一、工程領域可視化問題 ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類