[javaSE] 數據結構（AVL樹基本概念）

AVL樹是高度平衡的二叉樹，任何節點的兩個子樹的高度差別<=1

實現AVL樹

定義一個AVL樹，AVLTree，定義AVLTree的節點內部類AVLNode，節點包含以下特性：

1.key——關鍵字，對AVL樹的節點進行排序

2.left——左子樹

3.right——右子樹

4.height——高度

如果在AVL樹插入節點後可能導致AVL樹失去平衡，具體會有四種狀態：

LL：左左，LeftLeft

LR：左右，LeftRight

RL：右左，RightLeft

RR：右右，RightRight

解決上面的情況

解決LL，需要左單旋轉

解決RR，需要右單旋轉

解決LR，需要先右單旋轉，再左單旋轉

解決RL，需要先左單旋轉，再右單旋轉

實現左單旋轉

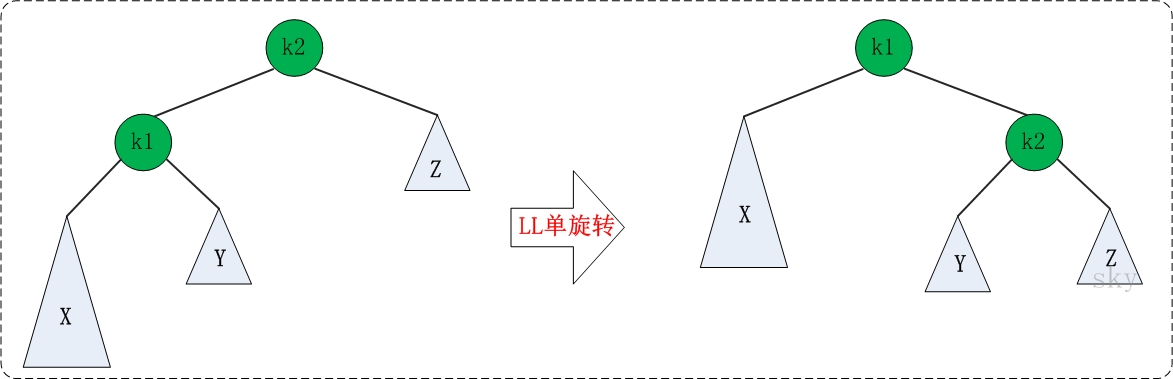
k1，k2

k2的left給k1

k1的right給k2的left

k2給k1的right

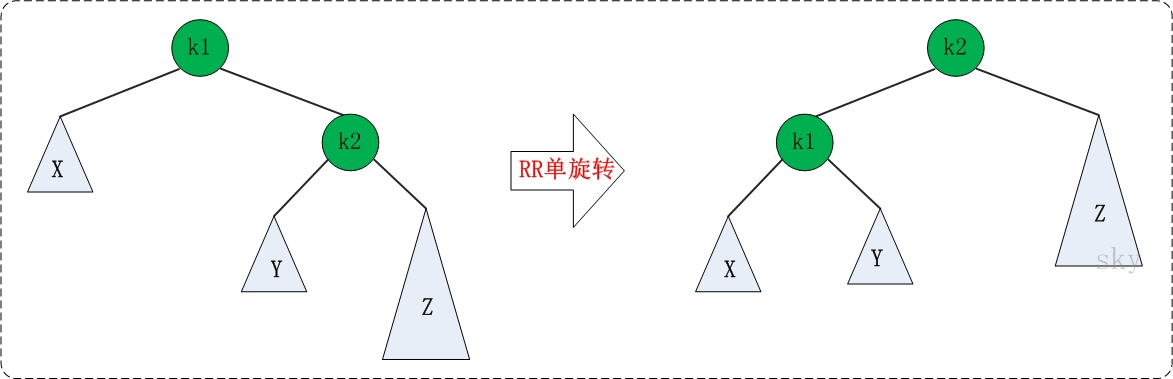
實現右單旋轉

k1，k2

k1的right給k2

k2的left給k1的right

k1給k2的left

節點的高度，是它左子樹或者右子樹中，高度大的那個 再加1

/**
 * AVL樹測試
 * @author taoshihan
 * @param <T>
 *
 */
public class AVLTree<T extends Comparable<T>> {
    private AVLNode mRoot;//根節點
    class AVLNode<T extends Comparable<T>>{
        private T key;//鍵值
        private int height;//高度
        private AVLNode left;//左子樹
        private AVLNode right;//右子樹
        public AVLNode(T key,AVLNode left,AVLNode right) {
            this.key=key;
            this.left=left;
            this.right=right;
            this.height=0;
        }
    }
    /**
     * 獲取節點高度
     * @param tree
     * @return
     */
    public int height(AVLNode<T> tree){
        if(tree!=null){
            return tree.height;
        }
        return 0;
    }
    /**
     * 取出左右子樹中高的那個
     * @param a
     * @param b
     * @return
     */
    public int maxHeight(int a,int b){
        return a>b ? a : b;
    }
    /**
     * 左單旋轉
     * @param k2
     * @return
     */
    public AVLNode<T> leftLeftRotation(AVLNode<T> k2){
        AVLNode k1;
        k1 = k2.left;
        k2.left=k1.right;
        k1.right=k2;
        k2.height=maxHeight(height(k2.left), height(k2.right));
        k1.height=maxHeight(height(k1.left), height(k1.right));
        return k1;
    }
    /**
     * 右單旋轉
     * @param k2
     * @return
     */
    public AVLNode<T> rightRightRotation(AVLNode<T> k1){
        AVLNode k2;
        k2=k1.right;
        k1.right=k2.left;
        k2.left=k1;
        
        k2.height=maxHeight(height(k2.left), height(k2.right));
        k1.height=maxHeight(height(k1.left), height(k1.right));
        return k2;
    }