在我們描述堆之前，我們首先要明白一個概念，什麼是樹？

樹的概念及結構

1.樹的概念

樹是一種非線性的數據結構，它是由n（n>=0）個有限結點組成一個具有層次關係的集合。把它叫做樹是因為它看起來像一棵倒掛的樹，也就是說它是根在上，而葉在下的。

有一個特殊的結點，稱為根結點，根節點沒有前驅結點。除根節點外，其餘結點被分成m(m > 0)個互不相交的集合T1、T2、…… 、Tm，其中每一個集合Ti(1 <= i <= m)又是一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅，但可以有0個或多個後繼。

由此可知，樹是遞歸定義的。

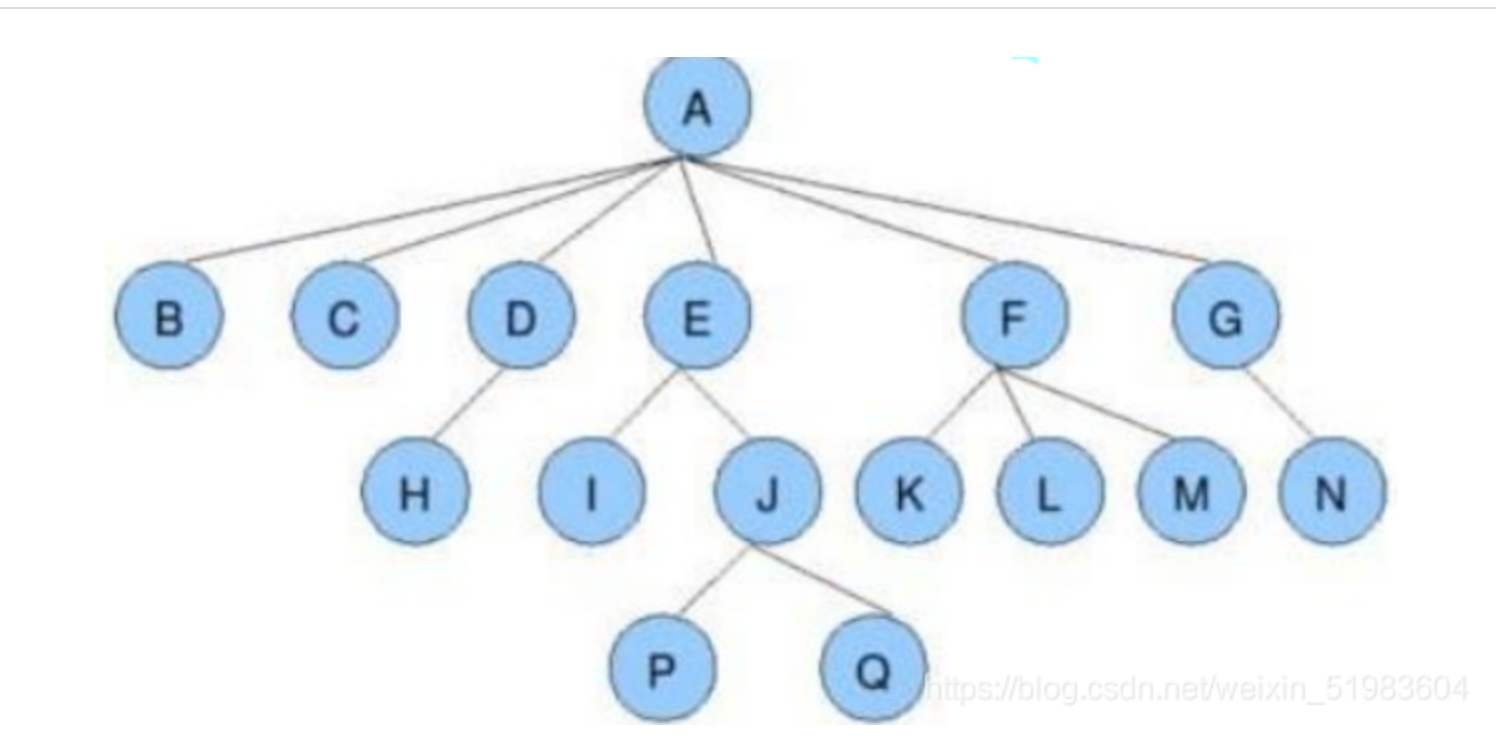
下麵介紹一些與樹相關的概念（以上面的樹為例）：

（1）結點的度：一個節點含有的子樹的個數稱為該節點的度；如上圖：A的為6，即B、C、D、E、F、G。

（2）葉結點：度為0的節點稱為葉結點；如上圖：B、C、H、I、K、L、M、N、P、Q 為葉結點。

（3）雙親結點或父結點：若一個節點含有子結點，則這個結點稱為其子結點的父結點；如上圖：A是B的父結點。

（4）孩子結點或子結點：一個結點含有的子樹的根結點稱為該結點的子結點；如上圖：B是A的孩子節點。

（5）兄弟結點：具有相同父結點的結點互稱為兄弟結點； 如上圖：B、C是兄弟結點。

（6）樹的度：一棵樹中，最大的節點的度稱為樹的度； 如上圖：樹的度為6。

（7）結點的層次：從根開始定義起，根為第1層，根的子結點為第2層，以此類推。

（8）樹的高度或深度：樹中結點的最大層次； 如上圖：樹的高度為4。

（9）節點的祖先：從根到某一結點所經分支上的所有結點；如上圖：D、A是H的祖先；A是所有結點的公共祖先。

（10）子孫：以某節點為根的子樹中任一節點都稱為該節點的子孫。如上圖：所有節點都是A的子孫。

（11）森林：多棵互不相交的樹的集合稱為森林。

2.樹的表示方法

樹由於不是線性結構，所以相對線性表，要存儲、表示就相對麻煩，實際中樹有很多種表示方式，如：雙親表示法，孩子表示法、孩子兄弟表示法等等。這裡簡單地介紹其中最常用的孩子兄弟表示法。

孩子兄弟表示法就是用孩子結點來找到下一層的結點，用兄弟結點來找到這一層其餘的結點，結構如下。

typedef int DataType;
struct Node
{
    struct Node* firstChild1; // 第一個孩子結點
    struct Node* pNextBrother; // 指向其下一個兄弟結點
    DataType data; // 結點中的數據域
};

二叉樹

1.二叉樹概念及結構

概念：一棵二叉樹是結點的一個有限集合，該集合為空，或者是由一個根節點加上兩棵稱為左子樹和右子樹的二叉樹組成。

二叉樹的特點：

（1）每個結點最多有兩棵子樹，即二叉樹不存在度大於2的結點。
（2）二叉樹的子樹有左右之分，其子樹的次序不能顛倒。

結構
特殊的二叉樹：

（1）滿二叉樹(Perfect Binary Tree)

每一層的結點數都達到最大值，則這個二叉樹就是滿二叉樹。
也就是說，如果一個二叉樹的層數為K（根節點是第1層），且結點總數是(2^k) -1 ，則它就是滿二叉樹，也稱為完美二叉樹

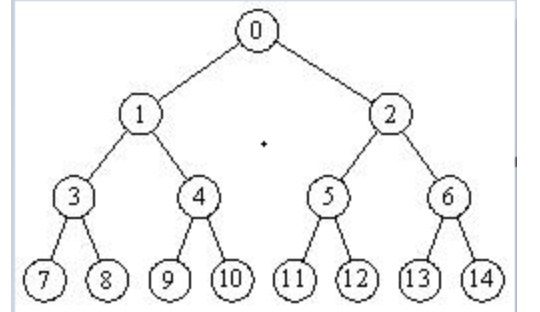
（2）完全二叉樹(Complete Binary Tree)

完全二叉樹是由滿二叉樹而引出來的。對於深度為K的、有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。 滿二叉樹是一種特殊的完全二叉樹。
完全二叉樹的葉子結點只能出現在最下層和次下層，且最下層的葉子結點從左到右連續；前K-1層是滿的二叉樹。

換句話說，完全二叉樹從根結點到倒數第二層滿足完美二叉樹，最後一層可以不完全填充，其葉子結點都靠左對齊。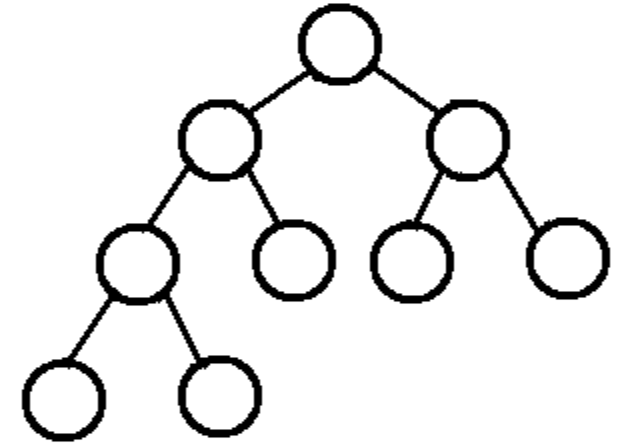

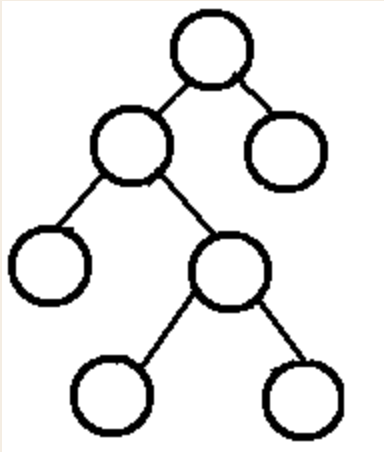
（3）完滿二叉樹(Full Binary Tree)

換句話說，所有非葉子結點的度都是2。（只要你有孩子，你就必然是有兩個孩子。） 

註：Full Binary Tree又叫做Strictly Binary Tree。

什麼是堆？

堆（英語：heap)是電腦科學中一類特殊的數據結構的統稱。堆通常是一個可以被看做一棵樹的數組對象。堆總是滿足下列性質：

• 堆中某個節點的值總是不大於或不小於其父節點的值；

• 堆總是一棵完全二叉樹。
  將根節點最大的堆叫做最大堆或大根堆，根節點最小的堆叫做最小堆或小根堆。常見的堆有二叉堆、斐波那契堆等。

堆是非線性數據結構，相當於一維數組，有兩個直接後繼。

堆的定義如下：n個元素的序列{k1,k2,ki,…,kn}當且僅當滿足下關係時，稱之為堆。

(ki <= k2i,ki <= k2i+1)或者(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)

若將和此次序列對應的一維數組（即以一維數組作此序列的存儲結構）看成是一個完全二叉樹，則堆的含義表明，完全二叉樹中所有非終端結點的值均不大於（或不小於）其左、右孩子結點的值。由此，若序列{k1,k2,…,kn}是堆，則堆頂元素（或完全二叉樹的根）必為序列中n個元素的最小值（或最大值）。
註意： 在二叉樹中，若當前節點的下標為 i， 則其父節點的下標為 i/2，其左子節點的下標為 i*2，其右子節點的下標為i*2+1；

堆的插入：
每次插入都是將先將新數據放在數組最後，由於從這個新數據的父結點到根結點必然為一個有序的序列，現在的任務是將這個新數據插入到這個有序序列中——這就類似於直接插入排序中將一個數據併入到有序區間中。

我們通過一個插入例子來看看插入操作的細節。我們將數字 16 插入到這個堆中：

堆的數組是： [ 10, 7, 2, 5, 1 ]。

第一步是將新的元素插入到數組的尾部，數組變成：[ 10, 7, 2, 5, 1, 16 ]；

相應的樹變成了：

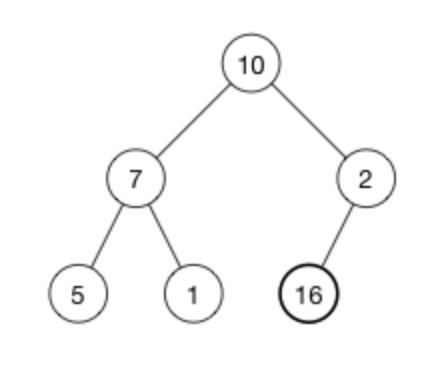
16 被添加最後一行的第一個空位。

不行的是，現在堆屬性不滿足，因為 2 在 16 的上面，我們需要將大的數字在上面（這是一個最大堆）

為了恢復堆屬性，我們需要交換 16 和 2。

現在還沒有完成，因為 10 也比 16 小。我們繼續交換我們的插入元素和它的父節點，直到它的父節點比它大或者我們到達樹的頂部。這就是所謂的 shift-up，每一次插入操作後都需要進行。它將一個太大或者太小的數字“浮起”到樹的頂部。

最後我們得到的堆：

現在每一個父節點都比它的子節點大。

堆的刪除：
堆中每次都只能刪除堆頂元素。為了便於重建堆，實際的操作是將最後一個數據的值賦給根結點，然後再從根結點開始進行一次從上向下的調整。調整時先在左右子結點中找最小的，如果父結點比這個最小的子結點還小說明不需要調整了，反之將父結點和它交換後再考慮後面的結點。相當於根結點數據的“下沉”過程。

我們將這個樹中的 (10) 刪除：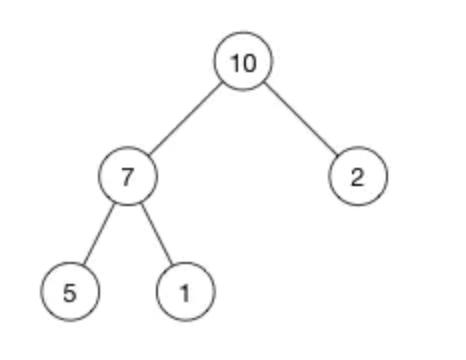

現在頂部有一個空的節點，怎麼處理？

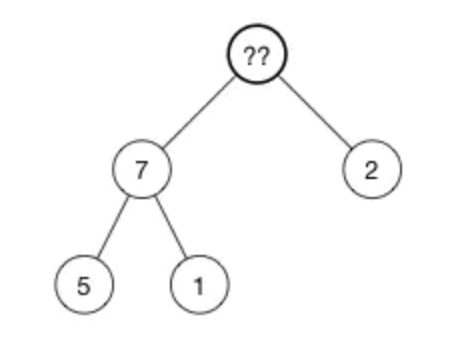
當插入節點的時候，我們將新的值返給數組的尾部。現在我們來做相反的事情：我們取出數組中的最後一個元素，將它放到樹的頂部，然後再修複堆屬性。

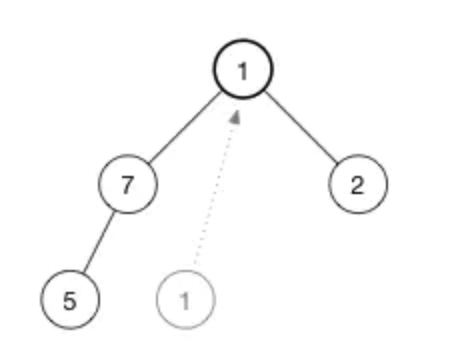
 現在來看怎麼 shift-down (1)。為了保持最大堆的堆屬性，我們需要樹的頂部是最大的數據。現在有兩個數字可用於交換 7 和 2。我們選擇這兩者中的較大者稱為最大值放在樹的頂部，所以交換 7 和 1，現在樹變成了：

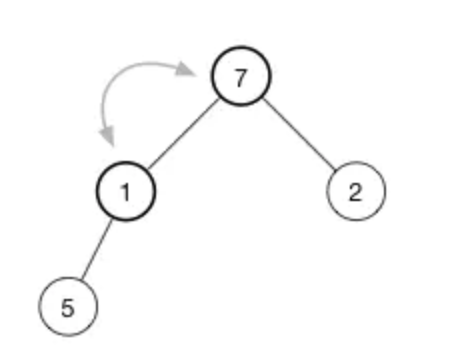
繼續堆化直到該節點沒有任何子節點或者它比兩個子節點都要大為止。對於我們的堆，我們只需要再有一次交換就恢復了堆屬性：

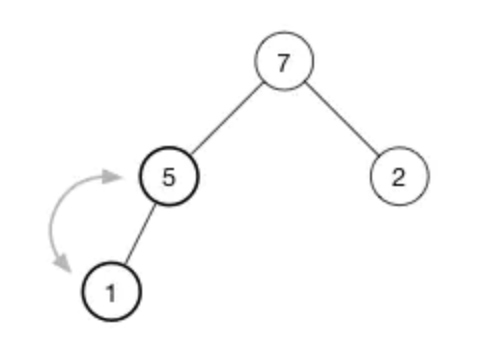
最大堆：

1.構造最大堆

原始數據為a[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7}，採用順序存儲方式，對應的完全二叉樹如下圖所示：

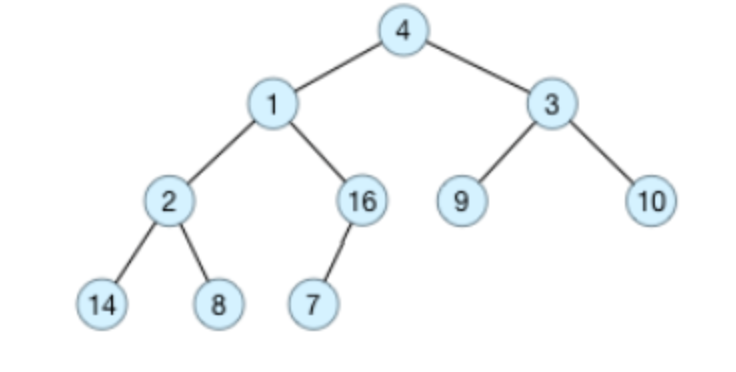
基本思想：
首先將每個葉子節點視為一個堆，再將每個葉子節點與其父節點一起構造成一個包含更多節點的對。所以，在構造堆的時候，首先需要找到最後一個節點的父節點，從這個節點開始構造最大堆；直到該節點前面所有分支節點都處理完畢，這樣最大堆就構造完畢了。
假設樹的節點個數為n，以1為下標開始編號，直到n結束。對於節點i，其父節點為i/2；左孩子節點為i*2，右孩子節點為i*2+1。最後一個節點的下標為n，其父節點的下標為n/2。
我們邊針對上邊數組操作如下圖所示，最後一個節點為7，其父節點為16，從16這個節點開始構造最大堆；構造完畢之後，轉移到下一個父節點2，直到所有父節點都構造完畢。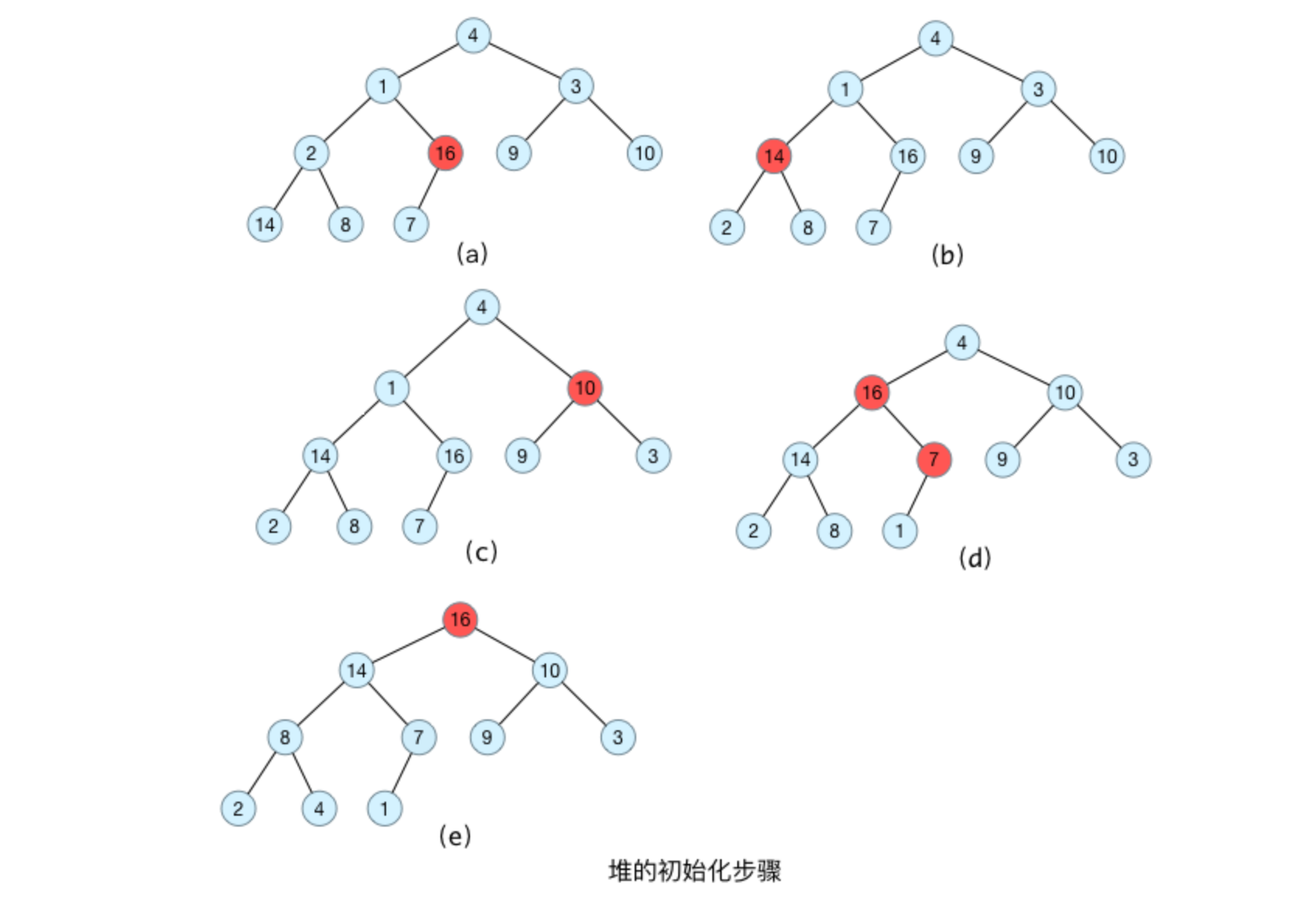

 代碼實現如下：

strcut MaxHeap
{
    Etype *heap; //數據元素存放的空間，下標從1開始存數數據，下標為0的作為工作空間，存儲臨時數據
    int HeapSize;//數據元素的個數
    int MaxSize; //存放數據元素空間的大小
};
MaxHeap H;
 
void MaxHeapInit (MaxHeap &H)
{
    for(int i = H.HeapSize/2; i>=1; i--)
    {
        H.heap[0] = H.heap[i];
        int son = i*2;
        while(son <= H.HeapSize)
        {
            if(son < H.HeapSize && H.heap[son] < H.heap[son+1])
                son++;
            if(H.heap[0] >= H.heap[son])
                break;
            else
            {
                H.heap[son/2] = H.heap[son];
                son *= 2;
            }
        }
        H.heap[son/2] = H.heap[0];
    }
}

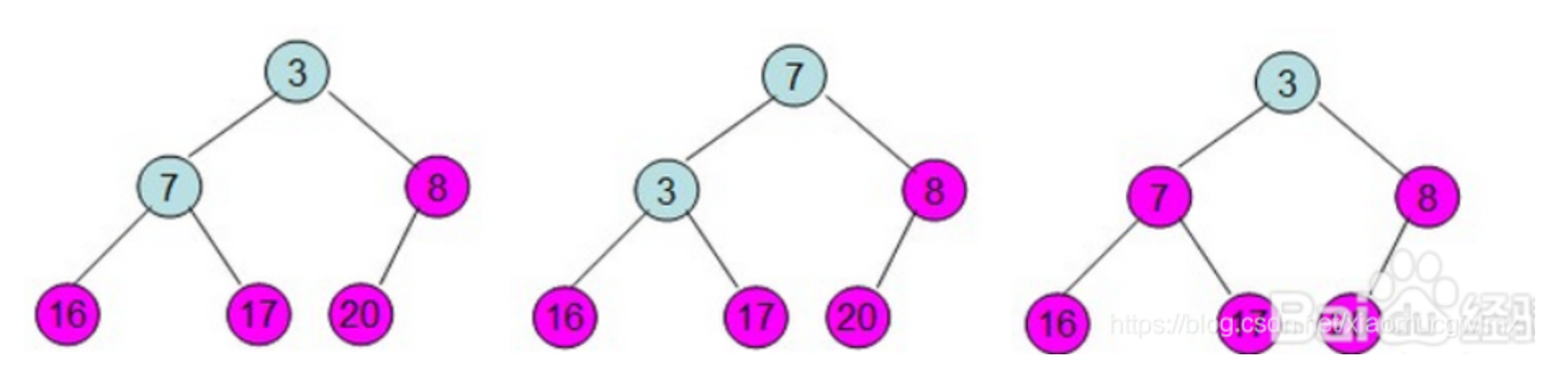
給定一個整形數組a[]={16,7,3,20,17,8}，對其進行堆排序。

堆排序是藉助堆來實現的選擇排序，思想同簡單的選擇排序，以下以大頂堆為例。註意：如果想升序排序就使用大頂堆，反之使用小頂堆。原因是堆頂元素需要交換到序列尾部。

　　首先，實現堆排序需要解決兩個問題：

　　1. 如何由一個無序序列鍵成一個堆？

　　2. 如何在輸出堆頂元素之後，調整剩餘元素成為一個新的堆？

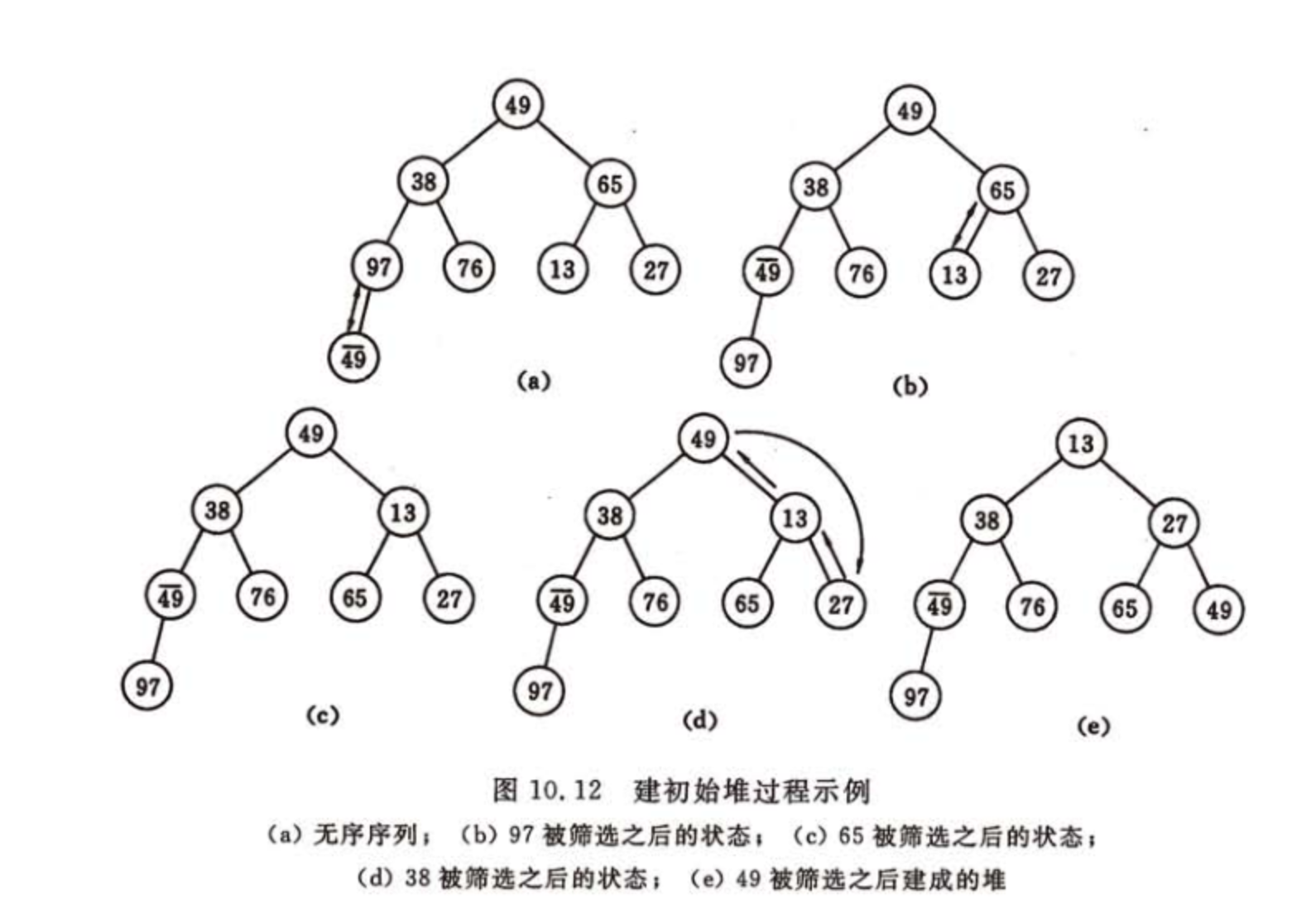
　　第一個問題，可以直接使用線性數組來表示一個堆，由初始的無序序列建成一個堆就需要自底向上從第一個非葉元素開始挨個調整成一個堆。

　　第二個問題，怎麼調整成堆？首先是將堆頂元素和最後一個元素交換。然後比較當前堆頂元素的左右孩子節點，因為除了當前的堆頂元素，左右孩子堆均滿足條件，這時需要選擇當前堆頂元素與左右孩子節點的較大者（大頂堆）交換，直至葉子節點。我們稱這個自堆頂自葉子的調整成為篩選。

　　從一個無序序列建堆的過程就是一個反覆篩選的過程。若將此序列看成是一個完全二叉樹，則最後一個非終端節點是n/2取底個元素，由此篩選即可。舉個慄子：

49,38,65,97,76,13,27,49序列的堆排序建初始堆和調整的過程如下：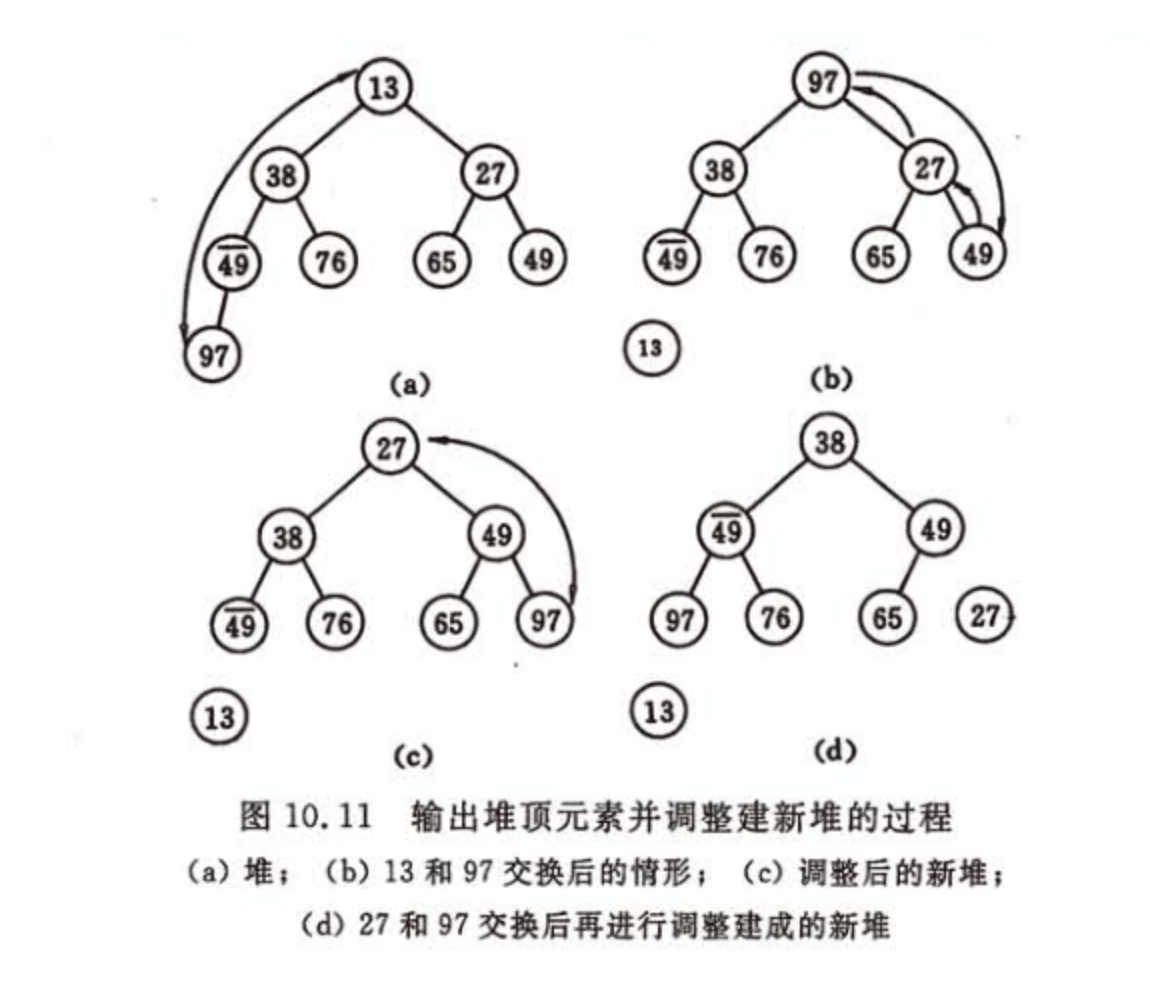

動圖演示:
（1）動畫從一排數字開始

（2）先將一排數字放入數組（這個數組看做堆），顯然這個堆是不滿足條件的

（3）從最後一個父節點開始對堆進行調整（heapify）使其滿足堆的性質（綠色代表調整好了，淺藍色表示正在調整）

（4）堆構建結束後將堆頂元素與最後一個節點交換，將最大值放在最後（紅色元素），剩下的n-1個元素堆的性質被破壞，需要重新做一次heapify使前n-1個元素滿足堆的性質，從而迴圈（4）這個過程實現堆排序

首先根據該數組元素構建一個完全二叉樹，具體過程如下(從左到右，從上到下按順序一步一步的詳細過程)：

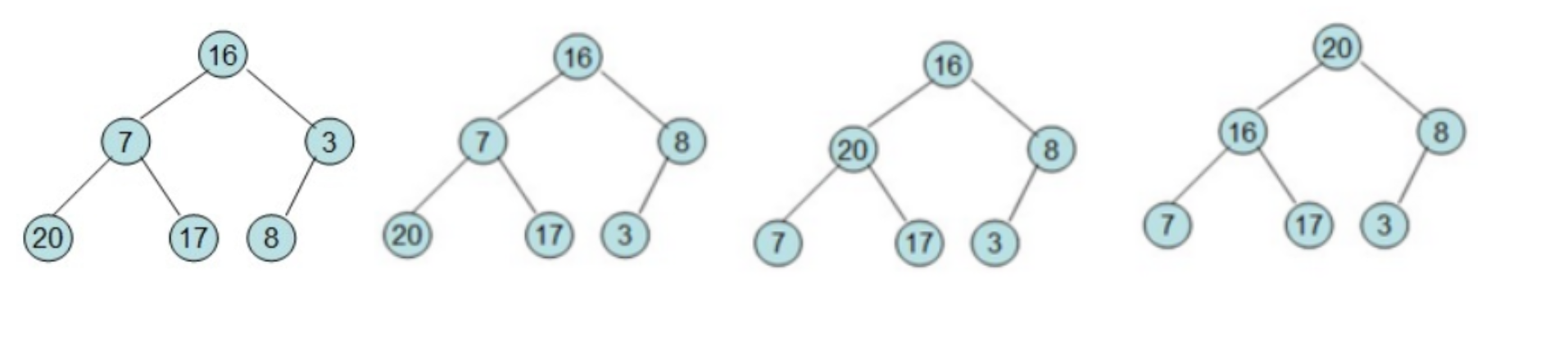
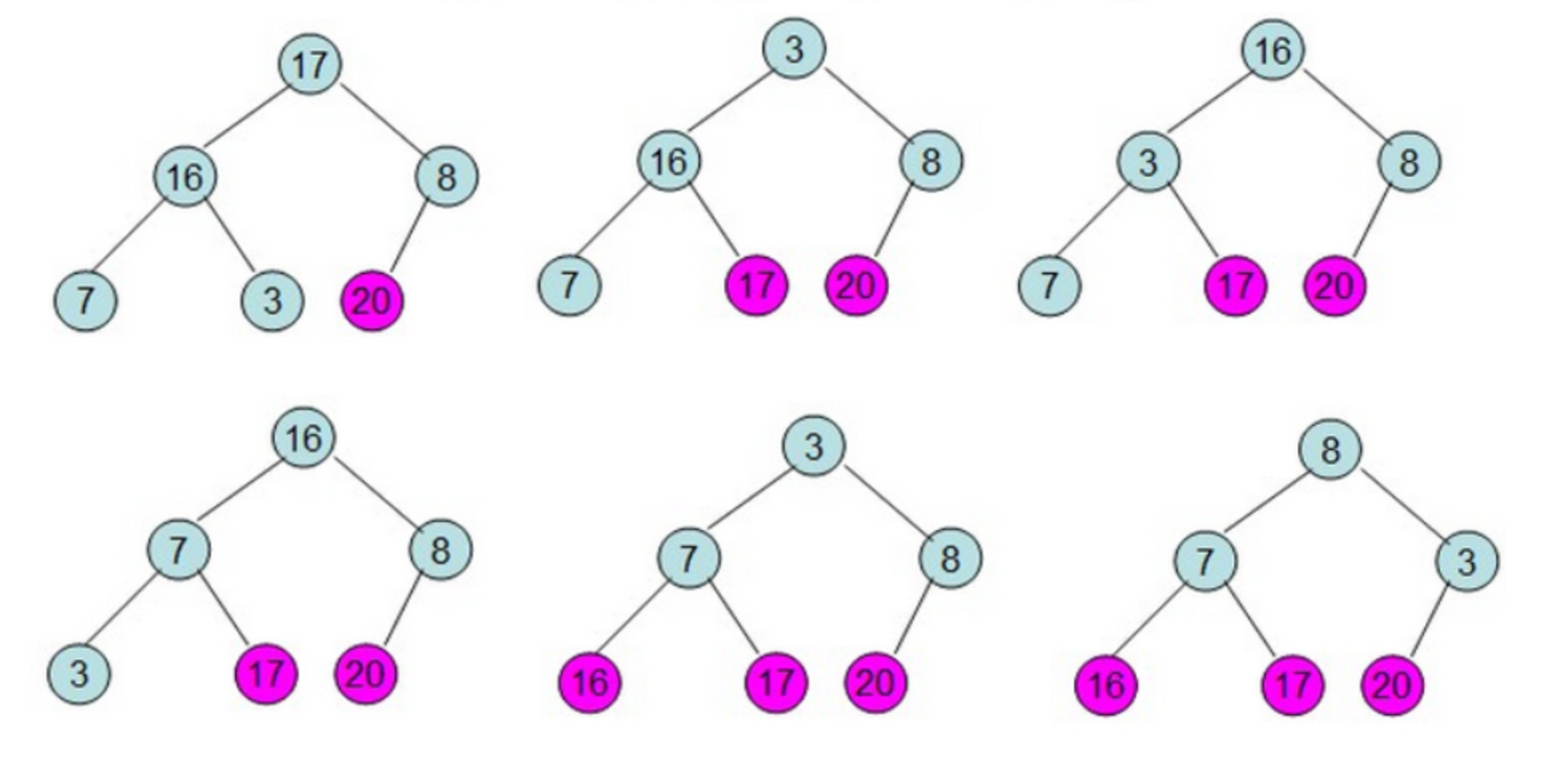
2.最大堆插入節點

最大堆的插入節點的思想就是先在堆的最後添加一個節點，然後沿著堆樹上升。跟最大堆的初始化過程大致相同。

void MaxHeapInsert (MaxHeap &H, EType &x)
{
	if(H.HeapSize == H.MaxSize)
		return false;
	int i = ++H.HeapSize;
	while(i!=1 && x>H.heap[i/2])
	{
		H.heap[i] = H.heap[i/2];
		i = i/2;
	}
	H.heap[i] = x;
	return true;
}

3.最大堆堆頂節點刪除

最大堆堆頂節點刪除思想如下：將堆樹的最後的節點提到根結點，然後刪除最大值，然後再把新的根節點放到合適的位置。

void MaxHeapDelete (MaxHeap &H, EType &x)
{
	if(H.HeapSize == 0)
		return false;
	x = H.heap[1];
	H.heap[0] = H.heap[H.HeapSize--];
	int i = 1, son = i*2; 
 
	while(son <= H.HeapSize)
	{
		if(son <= H.HeapSize && H.heap[0] < H.heap[son+1])
			son++;
		if(H.heap[0] >= H.heap[son])
			break;
		H.heap[i] = H.heap[son];
		i = son;
		son  = son*2;
	}
	H.heap[i] = H.heap[0];
	return true;
}

最小堆

整體操作和最大堆類似，這裡不做贅述。

應用場景：

海量數據中找出前k大數（topk問題）

先拿10000個數建堆，然後依次添加剩餘元素，如果大於堆頂的數（10000中最小的），將這個數替換堆頂，並調整結構使之仍然是一個最小堆，這樣，遍歷完後，堆中的10000個數就是所需的最大的10000個。建堆時間複雜度是O（mlogm），演算法的時間複雜度為O（nmlogm）（n為10億，m為10000）。

優化的方法：可以把所有10億個數據分組存放，比如分別放在1000個文件中。這樣處理就可以分別在每個文件的10^6個數據中找出最大的10000個數，合併到一起在再找出最終的結果。

下麵整理一下這方面的問題：

top K問題
在大規模數據處理中，經常會遇到的一類問題：在海量數據中找出出現頻率最好的前k個數，或者從海量數據中找出最大的前k個數，這類問題通常被稱為top K問題。例如，在搜索引擎中，統計搜索最熱門的10個查詢詞；在歌曲庫中統計下載最高的前10首歌等。
針對top K類問題，通常比較好的方案是分治+Trie樹/hash+小頂堆（就是上面提到的最小堆），即先將數據集按照Hash方法分解成多個小數據集，然後使用Trie樹活著Hash統計每個小數據集中的query詞頻，之後用小頂堆求出每個數據集中出現頻率最高的前K個數，最後在所有top K中求出最終的top K。

例如：有1億個浮點數，如果找出其中最大的10000個？
最容易想到的方法是將數據全部排序，然後在排序後的集合中進行查找，最快的排序演算法的時間複雜度一般為O（nlogn），如快速排序。但是在32位的機器上，每個float類型占4個位元組，1億個浮點數就要占用400MB的存儲空間，對於一些可用記憶體小於400M的電腦而言，很顯然是不能一次將全部數據讀入記憶體進行排序的。其實即使記憶體能夠滿足要求（我機器記憶體都是8GB），該方法也並不高效，因為題目的目的是尋找出最大的10000個數即可，而排序卻是將所有的元素都排序了，做了很多的無用功。

第二種方法為局部淘汰法，該方法與排序方法類似，用一個容器保存前10000個數，然後將剩餘的所有數字——與容器內的最小數字相比，如果所有後續的元素都比容器內的10000個數還小，那麼容器內這個10000個數就是最大10000個數。如果某一後續元素比容器內最小數字大，則刪掉容器內最小元素，並將該元素插入容器，最後遍歷完這1億個數，得到的結果容器中保存的數即為最終結果了。此時的時間複雜度為O（n+m^2），其中m為容器的大小，即10000。

第三種方法是分治法，將1億個數據分成100份，每份100萬個數據，找到每份數據中最大的10000個，最後在剩下的100*10000個數據裡面找出最大的10000個。如果100萬數據選擇足夠理想，那麼可以過濾掉1億數據裡面99%的數據。100萬個數據裡面查找最大的10000個數據的方法如下：用快速排序的方法，將數據分為2堆，如果大的那堆個數N大於10000個，繼續對大堆快速排序一次分成2堆，如果大的那堆個數N大於10000個，繼續對大堆快速排序一次分成2堆，如果大堆個數N小於10000個，就在小的那堆裡面快速排序一次，找第10000-n大的數字；遞歸以上過程，就可以找到第1w大的數。參考上面的找出第1w大數字，就可以類似的方法找到前10000大數字了。此種方法需要每次的記憶體空間為10^6*4=4MB，一共需要101次這樣的比較。

第四種方法是Hash法。如果這1億個書裡面有很多重覆的數，先通過Hash法，把這1億個數字去重覆，這樣如果重覆率很高的話，會減少很大的記憶體用量，從而縮小運算空間，然後通過分治法或最小堆法查找最大的10000個數。

第五種方法採用最小堆。首先讀入前10000個數來創建大小為10000的最小堆，建堆的時間複雜度為O（mlogm）（m為數組的大小即為10000），然後遍歷後續的數字，並於堆頂（最小）數字進行比較。如果比最小的數小，則繼續讀取後續數字；如果比堆頂數字大，則替換堆頂元素並重新調整堆為最小堆。整個過程直至1億個數全部遍歷完為止。然後按照中序遍歷的方式輸出當前堆中的所有10000個數字。該演算法的時間複雜度為O（nmlogm），空間複雜度是10000（常數）。

實際運行：
實際上，最優的解決方案應該是最符合實際設計需求的方案，在時間應用中，可能有足夠大的記憶體，那麼直接將數據扔到記憶體中一次性處理即可，也可能機器有多個核，這樣可以採用多線程處理整個數據集。

   下麵針對不容的應用場景，分析了適合相應應用場景的解決方案。

（1）單機+單核+足夠大記憶體
如果需要查找10億個查詢次（每個占8B）中出現頻率最高的10個，考慮到每個查詢詞占8B，則10億個查詢次所需的記憶體大約是10^9 * 8B=8GB記憶體。如果有這麼大記憶體，直接在記憶體中對查詢次進行排序，順序遍歷找出10個出現頻率最大的即可。這種方法簡單快速，使用。然後，也可以先用HashMap求出每個詞出現的頻率，然後求出頻率最大的10個詞。

（2）單機+多核+足夠大記憶體
這時可以直接在記憶體總使用Hash方法將數據劃分成n個partition，每個partition交給一個線程處理，線程的處理邏輯同（1）類似，最後一個線程將結果歸併。

    該方法存在一個瓶頸會明顯影響效率，即數據傾斜。每個線程的處理速度可能不同，快的線程需要等待慢的線程，最終的處理速度取決於慢的線程。而針對此問題，解決的方法是，將數據劃分成c×n個partition（c>1），
每個線程處理完當前partition後主動取下一個partition繼續處理，知道所有數據處理完畢，最後由一個線程進行歸併。

（3）單機+單核+受限記憶體
這種情況下，需要將原數據文件切割成一個一個小文件，如次啊用hash(x)%M，將原文件中的數據切割成M小文件，如果小文件仍大於記憶體大小，繼續採用Hash的方法對數據文件進行分割，知道每個小文件小於記憶體大小，這樣每個文件可放到記憶體中處理。採用（1）的方法依次處理每個小文件。

（4）多機+受限記憶體
這種情況，為了合理利用多台機器的資源，可將數據分發到多台機器上，每台機器採用（3）中的策略解決本地的數據。可採用hash+socket方法進行數據分發。

從實際應用的角度考慮，（1）（2）（3）（4）方案並不可行，因為在大規模數據處理環境下，作業效率並不是首要考慮的問題，演算法的擴展性和容錯性才是首要考慮的。演算法應該具有良好的擴展性，以便數據量進一步加大（隨著業務的發展，數據量加大是必然的）時，在不修改演算法框架的前提下，可達到近似的線性比；演算法應該具有容錯性，即當前某個文件處理失敗後，能自動將其交給另外一個線程繼續處理，而不是從頭開始處理。

top K問題很適合採用MapReduce框架解決，用戶只需編寫一個Map函數和兩個Reduce 函數，然後提交到Hadoop（採用Mapchain和Reducechain）上即可解決該問題。具體而言，就是首先根據數據值或者把數據hash(MD5)後的值按照範圍劃分到不同的機器上，最好可以讓數據劃分後一次讀入記憶體，這樣不同的機器負責處理不同的數值範圍，實際上就是Map。得到結果後，各個機器只需拿出各自出現次數最多的前N個數據，然後彙總，選出所有的數據中出現次數最多的前N個數據，這實際上就是Reduce過程。對於Map函數，採用Hash演算法，將Hash值相同的數據交給同一個Reduce task；對於第一個Reduce函數，採用HashMap統計出每個詞出現的頻率，對於第二個Reduce 函數，統計所有Reduce task，輸出數據中的top K即可。

直接將數據均分到不同的機器上進行處理是無法得到正確的結果的。因為一個數據可能被均分到不同的機器上，而另一個則可能完全聚集到一個機器上，同時還可能存在具有相同數目的數據。

以下是一些經常被提及的該類問題。

（1）有10000000個記錄，這些查詢串的重覆度比較高，如果除去重覆後，不超過3000000個。一個查詢串的重覆度越高，說明查詢它的用戶越多，也就是越熱門。請統計最熱門的10個查詢串，要求使用的記憶體不能超過1GB。

（2）有10個文件，每個文件1GB，每個文件的每一行存放的都是用戶的query，每個文件的query都可能重覆。按照query的頻度排序。

（3）有一個1GB大小的文件，裡面的每一行是一個詞，詞的大小不超過16個位元組，記憶體限制大小是1MB。返回頻數最高的100個詞。

（4）提取某日訪問網站次數最多的那個IP。

（5）10億個整數找出重覆次數最多的100個整數。

（6）搜索的輸入信息是一個字元串，統計300萬條輸入信息中最熱門的前10條，每次輸入的一個字元串為不超過255B，記憶體使用只有1GB。

（7）有1000萬個身份證號以及他們對應的數據，身份證號可能重覆，找出出現次數最多的身份證號。

重覆問題
在海量數據中查找出重覆出現的元素或者去除重覆出現的元素也是常考的問題。針對此類問題，一般可以通過點陣圖法實現。例如，已知某個文件內包含一些電話號碼，每個號碼為8位數字，統計不同號碼的個數。

本題最好的解決方法是通過使用點陣圖法來實現。8位整數可以表示的最大十進位數值為99999999。如果每個數字對應於點陣圖中一個bit位，那麼存儲8位整數大約需要99MB。因為1B=8bit，所以99Mbit摺合成記憶體為99/8=12.375MB的記憶體，即可以只用12.375MB的記憶體表示所有的8位數電話號碼的內容。

遞歸序：

value ==null ; return

node.left

node.right

1,2,4,4(left==null),4(right ==null),2,5,5(left==null),5(right ==null),2,1,3,6,6,6,3,7,7,7,3,1

先序（頭、左、右）第一次出現：1，2， 4，5，3，6，7

中序（左、頭、右）第二次出現：4，2，5，1，6，3，7

後序 （左、右、頭）第三次出現：4，5，2，6，7，3，1

任何遞歸函數都可以改為非遞歸函數。

  class Node<V>{
        V value;
        Node left;
        Node right;
    }

先序遍歷：

先把頭節點放到棧裡面，

1.每次在棧中彈出一個節點current

2.列印current

3.先壓右 再壓左，如果有的話。沒有什麼都不做。

4.重覆上面操作。

1節點 彈出，列印1 ，先壓3 再壓2，彈出2，列印2，先壓5，再壓4，彈出4 ，列印4，沒有什麼都不做。彈出5.

    public static void preOrderUnRecur(Node head){
        System.out.println("pre-order:");
        if(head != null){
            Stack<Node> stack = new Stack<Node>();
            stack.add(head);
            while (!stack.isEmpty()){
                head = stack.pop();
                System.out.println(head.value+"");
                if(head.right != null){
                    stack.push(head.right);
                }
                if(head.left != null){
                    stack.push(head.left);
                }
            }
        }
        System.out.println();
    }

後序遍歷：

1.當前節點current 彈出

2.把當前節點放到收集棧

3.先壓左，再壓右，沒有左右直接走

4.周而複始

5.收集完之後，單獨列印收集棧裡面的。

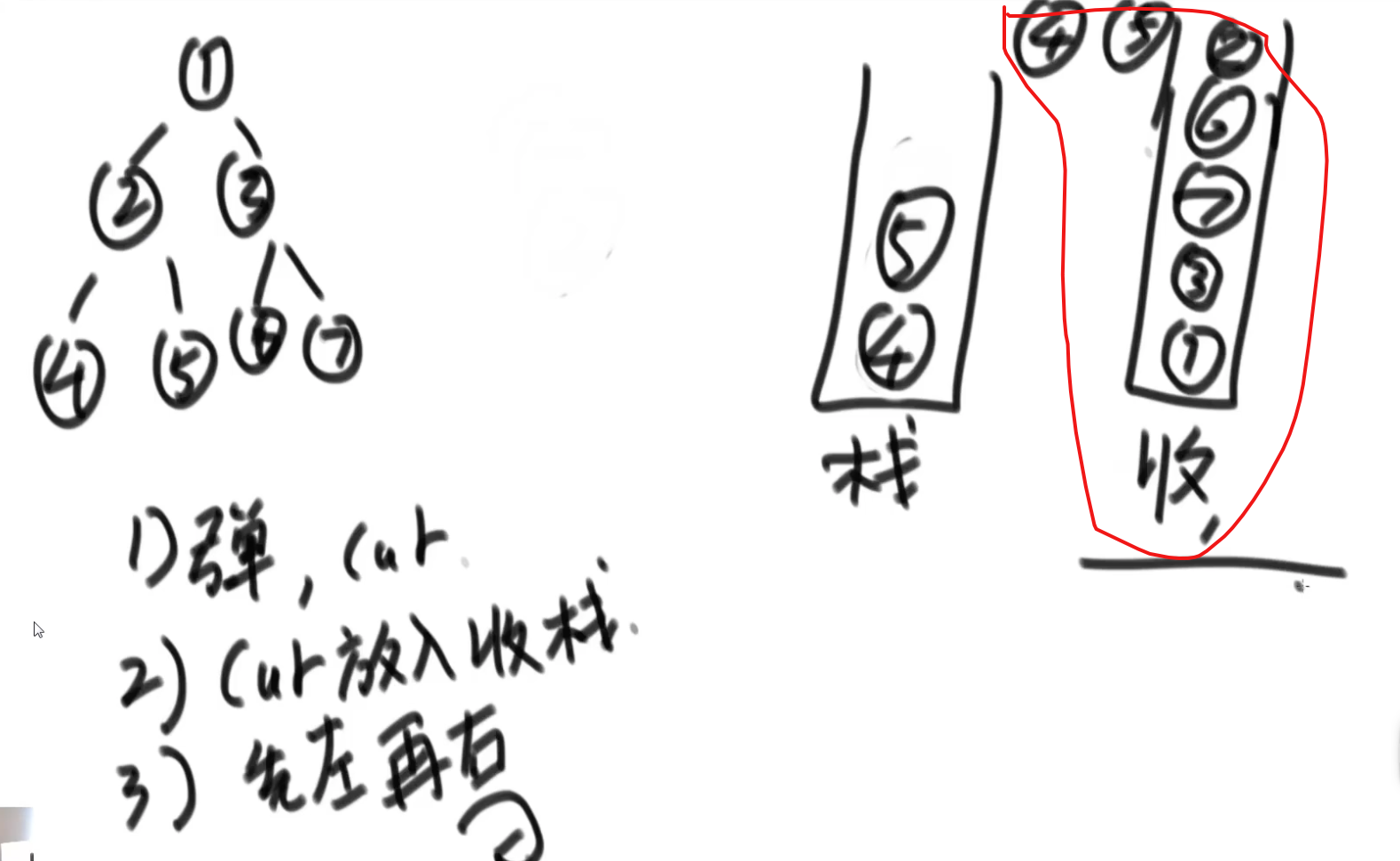
    //後序遍歷
    public static void posOrderUnRecur(Node head){
        System.out.println("pos-order:");
        if(head != null){
            Stack<Node> stack = new Stack<Node>();
            Stack<Node> newStack = new Stack<Node>();
            stack.push(head);
            while (!stack.isEmpty()){
                head = stack.pop();
                newStack.push(head);
                System.out.println(head.value+"");
                if(head.left!= null){
                    stack.push(head.left);
                }
                if(head.right!= null){
                    stack.push(head.right);
                }
            }
            while (!newStack.isEmpty()){
                System.out.println(newStack.pop().value +""); 
            }
        }
        System.out.println();
    }

 中序遍歷：

先左，再頭，再右 

每棵子樹 ，整棵樹左邊界進棧，依次彈出的過程中，列印，對彈出節點的右樹重覆。

4，2，5，1，6，3，7

1，2，4 進棧，每一次彈一個節點，4彈出，列印4 ，4 沒有右樹，彈出2，列印，2有右樹5，5 進棧，5 彈出，列印5 ，5沒有右樹，彈出1，列印1，1有右樹3，3，6 進棧。

彈出6，列印6 ，6沒有右樹，彈出3，列印3，3有右樹7，彈出7 列印7， 7無右樹，整個棧彈空。

    //中序遍歷
    public static void inOrderUnRecur(Node head){
        System.out.println("in-order:");
        if(head != null){
            Stack<Node> stack = new Stack<Node>();
            while (!stack.isEmpty() || head != null) {
                if (head != null) {
                    stack.push(head); //左邊界進棧
                    head = head.left;//左邊界全壓
                } else {
                    head = stack.pop();//沒有左邊界，彈出節點
                    System.out.println(head.value + "");
                    head = head.right;//移動到右 壓右
                }
            }
        }
        System.out.println();
    }

二叉樹的先序遍歷，就是深度遍歷。

寬度遍歷用隊列，先進先出。

先左 後右，

    public  static  void wide(Node head){
        if (head ==null) {
          return;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(head);
        while (!queue.isEmpty()){
            Node cur = queue.poll();
            System.out.println(cur.value);
            if(cur.left !=null){
                queue.add(cur.left);
            }
            if(cur.right !=null){
                queue.add(cur.right);
            }
        }
    }

求一棵二叉樹的最大寬度：

    public  static  int maxWidth(Node head){
        if (head ==null) {
          return 0;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(head);
        HashMap<Node,Integer> levelMap = new HashMap<>();
        levelMap.put(head,1);
        int curLevel = 1;
        int curLevelNodes = 0;
        int max = Integer.MIN_VALUE;
        while (!queue.isEmpty()){
            Node cur = queue.poll();
            int curNodeLevel = levelMap.get(cur);
            if(curNodeLevel == curLevel){
                curLevelNodes++;
            }else{
                max = Math.max(max,curLevelNodes);
                curLevel++;
                curLevelNodes = 1;
            }
          //  System.out.println(cur.value);
            if(cur.left !=null){
                levelMap.put(cur.left,curNodeLevel+1);
                queue.add(cur.left);
            }
            if(cur.right !=null){
                levelMap.put(cur.right,curNodeLevel+1);
                queue.add(cur.right);
            }
        }
        return  max;
    }