【collection】1.java容器之HashMap&LinkedHashMap&Hashtable

来源:https://www.cnblogs.com/cutter-point/archive/2022/12/02/16943518.html
-Advertisement-
Play Games

Map源碼剖析 HashMap&LinkedHashMap&Hashtable hashMap預設的閾值是0.75 HashMap put操作 put操作涉及3種結構，普通node節點，鏈表節點，紅黑樹節點，針對第三種，紅黑樹節點，我們後續單獨去學習，這裡不多做擴散 final V putVal(i ...


Map源碼剖析

HashMap&LinkedHashMap&Hashtable

hashMap預設的閾值是0.75

HashMap put操作

put操作涉及3種結構，普通node節點，鏈表節點，紅黑樹節點，針對第三種，紅黑樹節點，我們後續單獨去學習，這裡不多做擴散

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
			   boolean evict) {
	Node<K,V>[] tab; Node<K,V> p; int n, i;
	if ((tab = table) == null || (n = tab.length) == 0) {
		// 初始化哈希數組，或者對哈希數組擴容，返回新的哈希數組
		tab = resize();
		n = tab.length;
	}

	// 相當於取餘
	i = (n - 1) & hash;
	p = tab[i];
	if (p == null) {
		// 直接放普通元素
		tab[i] = newNode(hash, key, value, null);
	} else {
		Node<K,V> e; K k;
		if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) {
			// 存在同位元素，也就是出現了hash碰撞
			e = p;
		} else if (p instanceof TreeNode) {
			// 如果當前位置已經是紅黑樹節點，那麼就put紅黑色
			e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
		} else {
			// 遍歷哈希槽後面鏈接的其他元素（binCount統計的是插入新元素之前遍歷過的元素數量）
			// 這裡就是鏈表類型
			for (int binCount = 0; ; ++binCount) {
				// 後繼節點為空
				if ((e = p.next) == null) {
					// 拼接到後繼節點上
					p.next = newNode(hash, key, value, null);
					/**
					 * 哈希槽（鏈）上的元素數量增加到TREEIFY_THRESHOLD後，這些元素進入波動期，即將從鏈表轉換為紅黑樹
					 * 註意這個TREEIFY_THRESHOLD 是8，為什麼是8？？
					 * 每次遍歷一個鏈表，平均查找的時間複雜度是 O(n)，n 是鏈表的長度。由於紅黑樹有自平衡的特點，可以防止不平衡情況的發生，
					 * 所以可以始終將查找的時間複雜度控制在 O(log(n))。
					 * 最初鏈表還不是很長，所以可能 O(n) 和 O(log(n)) 的區別不大，但是如果鏈表越來越長，那麼這種區別便會有所體現。所以為了提升查找性能，需要把鏈表轉化為紅黑樹的形式。
					 * 鏈表查詢的時候使用二分查詢，平均查找長度為n/2，長度為8的時候，為4，而6/2 = 3
					 * 而如果是紅黑樹，那麼就是log(n) ，長度為8時候，log(8) = 3, log(6) =
					 * 這個時候我們發現超過8這個閾值之後，鏈表的查詢效率會越來越不如紅黑樹
					 */
					if (binCount >= TREEIFY_THRESHOLD - 1) {
						// -1 for 1st
						treeifyBin(tab, hash);
					}
					break;
				}
				// 判斷鏈表中的後繼原始是否hash碰撞，如果發生了hash碰撞break
				if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))
					break;
				p = e;
			}
		}
		// 如果存在同位元素（在HashMap中占據相同位置的元素）
		if (e != null) { // existing mapping for key
			V oldValue = e.value;
			// 判斷是否需要進行覆蓋取值,因為key相同，那麼直接取代，否則什麼也不操作
			if (!onlyIfAbsent || oldValue == null) {
				e.value = value;
			}
			afterNodeAccess(e);
			return oldValue;
		}
	}
	++modCount;
	if (++size > threshold)
		resize();
	afterNodeInsertion(evict);
	return null;
}

總結關鍵信息：

哈希槽（鏈）上的元素數量增加到TREEIFY_THRESHOLD後，這些元素進入波動期，即將從鏈表轉換為紅黑樹
註意這個TREEIFY_THRESHOLD 是8，為什麼是8？？
每次遍歷一個鏈表，平均查找的時間複雜度是 O(n)，n 是鏈表的長度。由於紅黑樹有自平衡的特點，可以防止不平衡情況的發生，
所以可以始終將查找的時間複雜度控制在 O(log(n))。
最初鏈表還不是很長，所以可能 O(n) 和 O(log(n)) 的區別不大，但是如果鏈表越來越長，那麼這種區別便會有所體現。所以為了提升查找性能，需要把鏈表轉化為紅黑樹的形式。
鏈表查詢的時候使用二分查詢，平均查找長度為n/2，長度為8的時候，為4，而6/2 = 3
而如果是紅黑樹，那麼就是log(n) ，長度為8時候，log(8) = 3, log(6) =
這個時候我們發現超過8這個閾值之後，鏈表的查詢效率會越來越不如紅黑樹

HashMap get，remove操作

除了紅黑樹的查找比較特殊，其餘的鏈表查找就是暴力搜索，只是平均下來找到一個元素的話是n/2

final Node<K,V> removeNode(int hash, Object key, Object value,
						   boolean matchValue, boolean movable) {
	Node<K,V>[] tab = table;
	Node<K,V> p;
	int n, index;
	if (tab != null && (n = tab.length) > 0 && (p = tab[index = (n - 1) & hash]) != null) {
		Node<K,V> node = null, e; K k; V v;
		if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) {
			// 找到節點，並且是首節點
			node = p;
		} else if ((e = p.next) != null) {
			if (p instanceof TreeNode) {
				node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
			} else {
				// 鏈表查詢，暴力搜索
				do {
					if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) {
						node = e;
						break;
					}
					p = e;
				} while ((e = e.next) != null);
			}
		}
		// 移除節點，可能只需要匹配hash和key就行，也可能還要匹配value，這取決於matchValue參數
		if (node != null && (!matchValue || (v = node.value) == value ||
							 (value != null && value.equals(v)))) {
			if (node instanceof TreeNode) {
				// 移除紅黑樹節點
				((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
			} else if (node == p) {
				// 移除首節點為後繼節點
				tab[index] = node.next;
			} else {
				// 鏈表斷開
				p.next = node.next;
			}
			++modCount;
			--size;
			afterNodeRemoval(node);
			return node;
		}
	}
	return null;
}

HashMap擴容

鏈表拆分，進入新的容器

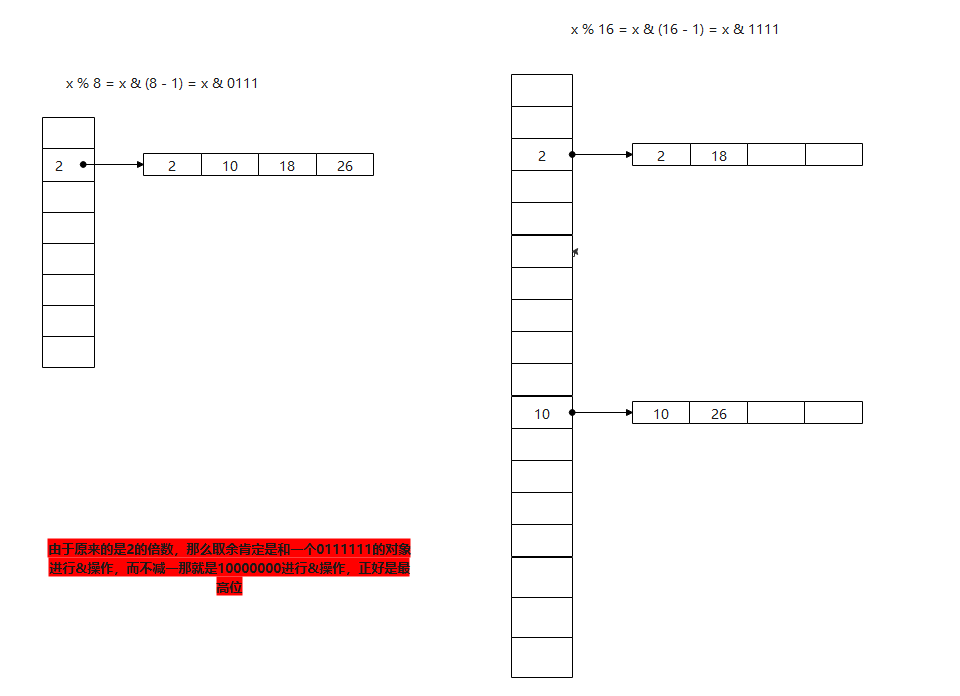
這裡有個知識點：如何使用位運算進行取模

a % b == a & (b - 1)

我們拆分鏈表的思路也是這樣：比如原來長度為8的鏈表，也就是 x % 8 = x & (8 - 1) = x & 0111 也就是取後三位，那麼擴容之後重新排序的話，容量擴大一倍，也就是16，那麼這個時候就是 x % 16 = x & (16 - 1) = x & 1111 這個時候我們發現和之前的區別就是最高位由原來的0變為1，如果還在後三位範圍內，那麼新容量中的位置是不會變的

final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    // 舊閾值
    int oldThr = threshold;
    int newCap, newThr = 0;
    if (oldCap > 0) {
        // 判斷舊容量是否已經超過最大值
        if (oldCap >= MAXIMUM_CAPACITY) {
            // 如果已經達到1 << 30;，那麼直接設置為Integer.MAX_VALUE;  0x7fffffff
            threshold = Integer.MAX_VALUE;
            return oldTab;
        } else {
            // mod by xiaof  嘗試將哈希表數組容量加倍，註意這裡是左移，也就是說*2
            newCap = oldCap << 1;
            // 如果容量成功加倍（沒有達到上限），則將閾值也加倍
            if (newCap < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY) {
                newThr = oldThr << 1;
            }
        }
        // else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
        //          oldCap >= DEFAULT_INITIAL_CAPACITY) {
        //     newThr = oldThr << 1; // double threshold
        // }
    } else if (oldThr > 0) {
        // initial capacity was placed in threshold
        newCap = oldThr;
    } else {               // zero initial threshold signifies using defaults
        // 如果實例化HashMap時沒有指定初始容量，則使用預設的容量與閾值
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }

    /*
         * 至此，如果newThr==0，則可能有以下兩種情形：
         * 1.哈希數組已經初始化，且哈希數組的容量還未超出最大容量，
         *   但是，在執行了加倍操作後，哈希數組的容量達到了上限
         * 2.哈希數組還未初始化，但在實例化HashMap時指定了初始容量
         */
    if (newThr == 0) {
        float ft = (float)newCap * loadFactor;
        // 如果新容量小於最大允許容量，並且新容量*裝載因數之後還是小於最大容量，那麼說明不需要擴容，那麼直接使用ft作為新的閾值容量
        // 如果新容量已經超過最大容量了，那麼就直接返回最大允許的容量
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    // 更新閾值
    threshold = newThr;
    // 新的容器對象，創建容量為新的newCap
    @SuppressWarnings({"rawtypes","unchecked"})
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];

    table = newTab;
    if (oldTab != null) {
        // 遍歷原來的數據，準備轉移到新的容器上
        for (int j = 0; j < oldCap; ++j) {
            // 獲取舊容器對象
            Node<K,V> e = oldTab[j];
            if (e != null) {
                // 把原來的數組中的指針設置為空
                oldTab[j] = null;
                if (e.next == null) {
                    // 重新計算hash索引位置，計算hash位置的方式防止數組越界的話，那麼就設置hashcode & 長度 - 1
                    newTab[e.hash & (newCap - 1)] = e;
                } else if (e instanceof TreeNode) {
                    // 紅黑樹，這裡是對紅黑樹進行拆分
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                } else { // preserve order
                    // lo對應的鏈表是數據不會動的
                    Node<K,V> loHead = null, loTail = null;
                    // hi對應的鏈表標識是需要去新容器新的位置的
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    // 這個是鏈表的情況下進行拆分
                    // 因為num % 2^n == num & (2^n - 1)，容量大小一定是2的N次方
                    do {
                        next = e.next;
                        // 註意：e.hash & oldCap，註意這裡是對老的容量oldCap進行計算這一步就是前面說的判斷多出的這一位是否為1
                        // 因為新的是老的2倍，新節點位置是否需要發生改變，取決於最高位是否為0
                        // 若與原容量做與運算，結果為0，表示將這個節點放入到新數組中，下標不變
                        // 由於原來的是2的倍數，那麼取餘肯定是和一個0111111的對象進行&操作，而不減一那就是10000000進行&操作，正好是最高位
                        if ((e.hash & oldCap) == 0) {
                            // 最高位為0，那麼位置不需要改變，本身就在原來容量範圍內的數據
                            // 直接加入lotail,並判斷是否需要初始化lotail
                            if (loTail == null) {
                                loHead = e;
                            } else {
                                loTail.next = e;
                            }
                            loTail = e;
                        } else {
                            // 最高位是1，那麼就需要進行切換位置
                            if (hiTail == null) {
                                hiHead = e;
                            } else {
                                hiTail.next = e;
                            }
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    // 最後返回最新的容器對象
    return newTab;
}

LinkedHashMap

基本和hashmap差不多，唯一需要註意下的是

還有一個核心點就是linkedHashMap覆蓋了newNode方法

Node<K,V> newNode(int hash, K key, V value, Node<K,V> e) {
	// 這裡創建了linkedhashmap對象
	LinkedHashMap.Entry<K,V> p = new LinkedHashMap.Entry<K,V>(hash, key, value, e);
	// 創建完成之後，就添加到鏈表中連接起來
	linkNodeLast(p);
	return p;
}

private void linkNodeLast(LinkedHashMap.Entry<K,V> p) {
	LinkedHashMap.Entry<K,V> last = tail;
	tail = p;
	if (last == null)
		head = p;
	else {
		p.before = last;
		last.after = p;
	}
}

插入覆蓋afterNodeAccess

void afterNodeAccess(Node<K,V> e) { // move node to last
	LinkedHashMap.Entry<K,V> last;
	if (accessOrder && (last = tail) != e) {
		// 獲取節點 b -> p -> a
		LinkedHashMap.Entry<K,V> p = (LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after;
		// 斷開尾部連接
		p.after = null;
		// 如果前置節點是空的，那麼就吧A作為head節點
		if (b == null) {
			head = a;
		} else {
			// 如果前置節點不為空，那麼就吧前置節點連接到後置節點，吧中間節點斷開
			b.after = a;
		}
		// 後置節點不為空，那麼就吧後置節點連接到前置節點上
		if (a != null) {
			a.before = b;
		} else {
			// 如果後置節點為空，那麼重新設置tail指向before節點
			last = b;
		}
		// 重新連接當前這個節點到末尾
		if (last == null)
			head = p;
		else {
			p.before = last;
			last.after = p;
		}
		tail = p;
		++modCount;
	}
}

afterNodeInsertion在linkedhashmap中作用不大

/**
 *
 * +----+      +----+      +----+
 * | b  | ---> |  p | ---> | a  |
 * +----+      +----+      +----+
 * @param e
 */
void afterNodeRemoval(Node<K,V> e) { // unlink
	// 移除節點
	LinkedHashMap.Entry<K,V> p = (LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after;
	p.before = p.after = null;
	if (b == null) {
		head = a;
	} else {
		b.after = a;
	}
	if (a == null) {
		tail = b;
	} else {
		a.before = b;
	}
}

綜上：linkedhashmap相對hashmap其實就是多加了一個鏈表把所有的數據關聯起來，只有在遍歷的時候才能體現出來有序，其他的操作是沒有差別的

關於hashtable

首先hashtable是線程安全的，因為它所有的函數都加上了synchronized

鏈表頭插法，沒有紅黑樹的轉換

初始化容量的時候預設是11，是奇數，而hashmap全都是2的冪次方

hashtable允許key為null

rehash函數

常用的hash函數是選一個數m取模（餘數），這個數在課本中推薦m是素數，但是經常見到選擇m=2n，因為對2n求餘數更快，並認為在key分佈均勻的情況下，key%m也是在[0,m-1]區間均勻分佈的。但實際上，key%m的分佈同m是有關的。

證明如下： key%m = key - xm，即key減掉m的某個倍數x，剩下比m小的部分就是key除以m的餘數。顯然，x等於key/m的整數部分，以floor(key/m)表示。假設key和m有公約數g，即key=ag, m=bg, 則 key - xm = key - floor(key/m)m = key - floor(a/b)m。由於0 <= a/b <= a，所以floor(a/b)只有a+1中取值可能，從而推導出key%m也只有a+1中取值可能。a+1個球放在m個盒子裡面，顯然不可能做到均勻。

由此可知，一組均勻分佈的key，其中同m公約數為1的那部分，餘數後在[0,m-1]上還是均勻分佈的，但同m公約數不為1的那部分，餘數在[0, m-1]上就不是均勻分佈的了。把m選為素數，正是為了讓所有key同m的公約數都為1，從而保證餘數的均勻分佈，降低衝突率。

protected void rehash() {
	int oldCapacity = table.length;
	Entry<?,?>[] oldMap = table;

	// overflow-conscious code
	// 這裡重新計算容量的辦法是容量擴大一倍，然後+1
	int newCapacity = (oldCapacity << 1) + 1;
	if (newCapacity - MAX_ARRAY_SIZE > 0) {
		if (oldCapacity == MAX_ARRAY_SIZE) {
			// Keep running with MAX_ARRAY_SIZE buckets
			return;
		}
		newCapacity = MAX_ARRAY_SIZE;
	}
	Entry<?,?>[] newMap = new Entry<?,?>[newCapacity];

	modCount++;
	threshold = (int)Math.min(newCapacity * loadFactor, MAX_ARRAY_SIZE + 1);
	table = newMap;

	// 重新把舊的原始轉移到新數組上
	for (int i = oldCapacity ; i-- > 0 ;) {
		for (Entry<K,V> old = (Entry<K,V>)oldMap[i] ; old != null ; ) {
			Entry<K,V> e = old;
			old = old.next;

			// 這裡因為容量是奇數，那麼就需要使用%取餘，而不是位運算 -》 a & (b - 1)
			int index = (e.hash & 0x7FFFFFFF) % newCapacity;
			e.next = (Entry<K,V>)newMap[index];
			newMap[index] = e;
		}
	}
}

參考

https://www.cnblogs.com/tuyang1129/p/12368842.html -- 鏈表拆分

https://www.cnblogs.com/lyhc/p/10743550.html - linkedhashmap

http://zhaox.github.io/algorithm/2015/06/29/hash


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 記憶體馬基礎知識
    javaweb三大組件 java web：Servlet，Filter，Listener 三大組件的各自功能： Servlet:用我的話來講它就像是一個處理器，它會接受http請求然後把他封裝成 HttpServletRequest 和HttpServletResponse 對象，然後進行處理 Fi ...
  • 前端和後端字元串比較的區別
    1,javaSript var str1="123"; var str2="123"; console.log(str1==str2);//true console.log(str1 str2);//true 這個沒什麼要說的 js裡面引入了嚴格執行的 符號,兩個等號和三個等號的區別在於 1,"== ...
  • odoo關於計算欄位store=True時導致的安裝/更新時間較長問題的解決方案
    Odoo安裝/更新模塊原理 Odoo每次安裝/更新模塊時，會進行以下幾步處理： 1.判斷是否需要創建表，如果需要創建且表不存在，則進行表的創建(不進行欄位的創建)； 2.獲取該表中已經存在的欄位； 3.獲取odoo模型中的所有欄位； 4.遍歷欄位，對需要存儲的欄位，進行欄位的更新/創建，欄位屬性的更 ...
  • 序章-準備工作
    前言 為什麼選擇自己開發一個詞典 市面上的詞典都不太彳亍，有Golden Dict和歐陸詞典這類註重詞典文件的，有有道詞典這類電子詞典，前者對於查詞更偏向於內容整合，後者則是釋義與例句。對於翻譯功能，兩者則都沒有整合，個人感覺很是麻煩，所以出於個人需要，決定自行開發。 開發的經歷 因為自己很喜歡UW ...
  • <一>智能指針基礎
    代碼1 int main(){ //裸指針,手動開闢,需要自己釋放,如果忘記了或者因為 //程式邏輯導致p沒有釋放,那麼就會導致記憶體泄漏 int *p=new int(10); if(***){ retur -1; } delete p; return 0; } 有沒有什麼辦法幫我們管理指針,確保資 ...
  • 【k哥爬蟲普法】爬取數據是否一定構成不正當競爭？
    我國目前並未出台專門針對網路爬蟲技術的法律規範，但在司法實踐中，相關判決已屢見不鮮，K 哥特設了“K哥爬蟲普法”專欄，本欄目通過對真實案例的分析，旨在提高廣大爬蟲工程師的法律意識，知曉如何合法合規利用爬蟲技術，警鐘長鳴，做一個守法、護法、有原則的技術人員。 案情介紹 谷米公司為開發和運營“酷米客”A ...
  • Android ViewPager2 + Fragment + BottomNavigationView 聯動
    Android ViewPager2 + Fragment + BottomNavigationView 聯動 本篇主要介紹一下 ViewPager2 + Fragment + BottomNavigationView , 上篇中把ViewPager2和Fragment 聯動起來了, 本篇主要把 B ...
  • 每日演算法之鏈表中環的入口結點
    JZ23 鏈表中環的入口結點 描述 給一個長度為n鏈表，若其中包含環，請找出該鏈表的環的入口結點，否則，返回null。 解析 環很大 在前面我們提到過快慢指針，判斷是否有環。如果有環，在來找環的入口。如果沒環直接返回null即可，我們假設是有環的，那麼會有兩種情況，一種是O型，一種是6型，其實原理都 ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類