進位制數及其相互轉換

来源:https://www.cnblogs.com/cs-whut/archive/2022/11/24/16919069.html
-Advertisement-
Play Games

之前我們已經知道什麼是 數組（一維數組）java 基礎——數組，數組的存取 這裡補充一點： 數組本身是引用數據類型 ，數組的元素 可以是 基本數據類型 跟 引用數據類型 那麼？什麼是二維數組 ？ 官方定義：以一維數組作為一維數組元素的數組 要是有點繞，不好理解，沒關係，簡單來說，就是一維數組裡面存一 ...


1.進位制數

        日常生活中人們都採用十進位數，十進位數用0、1、2、3、4、5、6、7、8、9十個數位表示數值；其基數為10，規則逢十進一，借一當十。

        電腦中採用二進位數，二進位數只用兩個數位0和1來表示數值；其基數為2，規則逢二進一，借一當二。

        由於二進位數書寫比較麻煩，因此，電腦中通常又用八進位數或十六進位數來書寫和表示信息。

        八進位數用0、1、2、3、4、5、6、7八個數位表示數值；其基數為8，規則逢八進一，借一當八。

        十六進位數用0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六個數位表示數值（在這十六個數位中的A、B、C、D、E、F六個數位，分別代表十進位數中的10、11、12、13、14、15，這是國際上通用的表示法）；其基數為16，規則逢十六進一，借一當十六。

        一般來說，若把它們統稱為 R進位，則R進位制具有下列特點：

        （1）在R進位中，具有R個數字元號，它們是0，l，…，（R- 1）。

        （2）在R進位中，由低位向高位是按“逢R進一”的規則進行計數。

        （3）R進位的基數是“R”，R進位數的第 i位的權為“Ri ”，約定整數最低位的位序號i為0（i=n，…2，l，0，-l，-2…）。

        基數和位權是進位制數的兩個要素。所謂某進位制的基數是指該進位制中允許選用的基本數位的個數。不同進位制具有不同的基數，基數表明瞭某一進位制的基本特征，例如對於二進位，有兩個數位（0，1），且由低位向高位是“逢二進一”，故其基數為2。對於某一進位制數，一個數位處在數的不同位置時，它所代表的數值是不同的。例如在十進位數333中，數字3在個位數位置上時表示3，即3×100；數字3在十位數位置上時表示30，即3×101；數字3在百位數位置上時表示300，即3×102。可見每個數位所表示的數值等於該數位乘以一個與數位所在位置有關的常數，這個常數叫位權。位權的大小是以基數為底、數位所在位置的序號為指數的整數次冪。位權表明瞭同一數字元號處於不同數位時所代表的值不同。

        一般而言，對於任意的R進位數

        An-1An-2…A1A0 . A-1A-2…A-m (其中n為整數位數，m為小數位數)

        可以表示為以下和式：

        An-1×Rn-1 +…+A1×R1+A0×R0+A-1×R-1+…A-m×R-m (其中R為基數)

        上式稱為“按權展開式”。

        我們可以用圓括弧外的下標值（如：10、2、8、16）表示該括弧內的數是哪一個進位制中的數，或在數的最後加上字母D（十進位、D可省略）、B（二進位）、Q（八進位）、H（十六進位）來區分其前面的數是屬於哪個進位制。例如，十進位數25可以表示為（25）10或25D或25；二進位數101可以表示為101B或（101）2 。

2．進位制數的相互轉換

        同一個數值可以用不同的進位制數表示，例如對於十進位數12，可以表示為二進位數1100，可以表示為八進位數14，也可以表示為十六進位數0C。這表明不同進位制只是表示數的不同手段，它們之間必定可以相互轉換。下麵具體介紹電腦中常用的幾種進位制數之間的轉換，即十進位與二進位數之間的轉換，十進位與八進位或十六進位數之間的轉換。

        （1）十進位數轉換為二進位數

        十進位數轉換為二進位數的基本方法是：對於整數採用“除2取餘”，對於小數採用“乘2取整”。具體做法為：對於十進位數整數，用2連續除要轉換的十進位整數及各次所得之商，直除到商等於0時為止，則各次所得之餘數即為所求二進位整數由低位到高位的值；對於十進位小數，用2連續乘要轉換的十進位小數及各次所得之積的小數部分，直乘到積的小數部分為0（或滿足所要求的精度）時為止，則各次所得之積的整數部分即為所求二進位小數由高位到低位的值。當十進位數包含有整數和小數兩部分時，可分別將整數和小數轉換，然後相加。

        例1  將十進位數53.375轉換成二進位數。

      

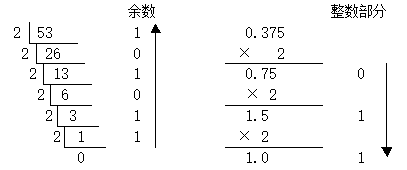
        於是， 53.375 = 110101.011B 。

        （2）二進位數轉換為十進位數

        二進位數轉換為十進位數的基本方法是將二進位數的各位按權展開相加。

        例2   將二進位數11011.101轉換成十進位數

        11011.101B =1×24+1×23+0×22+1×21+1×20+1×2-1+0×2-2+1×2-3

                            =16+8+0+2+1+0.5+0+0.125 =27.625

        於是， 11011.101B =27.625  。

【例1】逆序的二進位數

問題描述

把一個十進位整數轉換成二進位，然後將其二進位倒過來得到的新的數的十進位是多少?

例如，十進位整數6的二進位數為110，逆序後為011，去掉前導0，得到的新數為11，對應的十進位數為3。

輸入

輸入第1行為一個整數T（1≤T≤100），表示測試用例的組數。

之後T行，每行為1個十進位整數X（0≤X≤231−1）。

輸出

二進位數逆序後得到的新的十進位數。

輸入樣例

3

6

8

1

輸出樣例

3

1

1

         （1）編程思路。

        直接採用“除2取餘”的方法將輸入的十進位整數轉換為二進位數保存到a數組中，a[0]保存二進位數的最低位。之後將數組a中保存的二進位數位按權值展開即得到逆序後的十進位數。

        （2）源程式。

#include <stdio.h>
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        int a[32];
        int len=0;      // 保存n對應的二進位的位數
        while(n)        // 將n轉換為二進位數並保存到數組a中
        {
            a[len++] = n%2;
            n/=2;
        }
        int k;
        for (k=0;k<len && a[k]==0; k++) ;  // 去掉前導0
        int i,ans = 0;
        for (i=k;i<len;i++)     // 去掉前導0後，a[k]~a[len-1]正好是逆序後的二進位數
        {
            ans=ans*2+a[i];
        }
        printf("%d\n",ans);
    }
    return 0;
}

        將上面的源程式提交給“http://acm.hdu.edu.cn/showproblem.php?pid=5142  NPY and FFT”，可以Accepted。

        （3）十進位數轉換為R進位數

        類似於十進位數轉換為二進位數的方法，十進位數轉換為R進位數的基本方法是：對於整數採用“除R取餘”，對於小數採用“乘R取整”。具體做法為：對於十進位數整數，用R連續除要轉換的十進位整數及各次所得之商，直除到商等於0時為止，則各次所得之餘數即為所求R進位整數由低位到高位的值；對於十進位小數，用R連續乘要轉換的十進位小數及各次所得之積的小數部分，直乘到積的小數部分為0（或滿足所要求的精度）時為止，則各次所得之積的整數部分即為所求R進位小數由高位到低位的值。當十進位數包含有整數和小數兩部分時，可分別將整數和小數轉換，然後相加。

       （4）R進位數轉換為十進位數

        R進位數轉換為十進位數的基本方法是將R進位數的各位按權展開，然後進行十進位數相加即可。

【例2】十進位數轉換為M進位數

問題描述

將一個十進位數X(1<=X<=10^9)轉換成任意進位數M（2<=M<=16）。

輸入

一行兩個正整數X和M。

輸出

輸出X的M進位的表示。

輸入樣例

31 16

輸出樣例

1F

        （1）編程思路1。

          直接採用“除M取餘”的方法將十進位整數X轉換為M進位數。

        （2）源程式1。

#include <stdio.h>
#include <string.h>
char table[16]="0123456789ABCDEF";
int main()
{
    int x,m;
    scanf("%d%d",&x,&m);
    char num[33];
    int i,j,k=0;
    do {
        num[k++]=table[x%m];
        x/=m;
    } while (x!=0);
    num[k]='\0';
    for (i=0,j=k-1;i<j;i++,j--)
    {
        char ch;
        ch=num[i]; num[i]=num[j]; num[j]=ch;
    }
    printf("%s\n",num);
    return 0;
}

        （3）編程思路2。

        由於採用“除M取餘”時，所得M進位數是按餘數逆序排列的。因此，可以採用遞歸演算法完成轉換。

        （4）源程式2。

#include <stdio.h>
#include <string.h>
char table[16]="0123456789ABCDEF";
void change(int n,int m)
{
    if (n==0) return ;
    change(n/m,m);
    printf("%c",table[n%m]);
}
int main()
{
    int x,m;
    scanf("%d%d",&x,&m);
    if (x==0)
       printf("0\n");
    else
        change(x,m);
    return 0;
}

 【例3】A+B

問題描述

輸入兩個不超過8位的十六進位整數，求它們的和並轉換為十進位數輸出。

註：十六進位數中的10~15分別用大寫的英文字母A、B、C、D、E、F表示或小寫的英文字母a、b、c、d、e、f表示。

輸入

輸入包括多組測試用例，每組測試用例占1行，為兩個十六進位整數A和B。

輸出

對每組測試用例，輸出一行。為A+B的十進位數。

輸入樣例

1 9

A B

a b

輸出樣例

10

21

21

        （1）編程思路。 

          編寫函數int hex2dec(char hex[])將保存在字元串hex中的十六進位整數按權值展開，轉換為十進位整數作為函數值返回。

        （2）源程式。

#include <stdio.h>
#include <string.h>
int hex2dec(char hex[])
{
    int i,num,s=0;
    for (i=0;hex[i]!='\0';i++)
    {
        if (hex[i]>='0' && hex[i]<='9')
           num=hex[i]-'0';
        else if (hex[i]>='A' && hex[i]<='Z')
            num=hex[i]-'A'+10;
        else
            num=hex[i]-'a'+10;
        s=s*16+num;
    }
    return s;
}
int main()
{
    char a[10],b[10];
    while(scanf("%s%s",a,b)!=EOF)
    {
        int x;
         x=hex2dec(a)+hex2dec(b);
         printf("%d\n",x);
    }
    return 0;
}

        將上面的源程式提交給“http://acm.hdu.edu.cn/showproblem.php?pid=1720 A+B Coming”，可以Accepted。

【例4】可進行數制轉換的計算器

 問題描述

 某計算器能夠在不同數制之間進行轉換。該計算器顯示屏有7位，除了數字0到9之外，它的按鈕還包括大寫字母A到F，因此它將支持基數2至16的不同進位。

請為該計算器編寫不同進位的數的轉換程式。

輸入

輸入包含多組測試用例。每個測試用例占1行，每行將有三個數字。第一個數字是要轉換的數。第二個數字是要轉換的數的基數。第三個數字是要轉換後的數字的基數。

輸出

輸出將僅是計算器顯示屏上顯示的轉換後的數字。數字應在7位顯示屏中右對齊。如果數字太長而無法顯示在顯示屏上，則在顯示屏上右對齊輸出“ERROR”（不帶引號）。

輸入樣例

1111000[bk][bk]2[bk]10

1111000[bk][bk]2[bk]16

2102101[bk][bk]3[bk]10

2102101[bk][bk]3[bk]15

[bk][bk]12312[bk][bk]4[bk][bk]2

[bk][bk][bk][bk][bk]1A[bk]15[bk][bk]2

1234567[bk]10[bk]16

[bk][bk][bk]ABCD[bk]16[bk]15

輸出樣例

[bk][bk][bk][bk]120

[bk][bk][bk][bk][bk]78

[bk][bk][bk]1765

[bk][bk][bk][bk]7CA

[bk][bk]ERROR

[bk][bk]11001

[bk]12D687

[bk][bk][bk]D071

說明：樣例中的一個“[bk]”僅表示一個空格，實際的輸入和輸出時就是一個空格。

        （1）編程思路。

        為完成基數為A的整數X轉換為基數為B的整數Y。可以先採用X按權值展開的方式將X轉換為十進位整數Z，再將十進位整數Z按“除B取餘”的方法轉換為B進位的整數Y。

        （2）源程式。

#include <stdio.h>
int main()
{
    char str[10];
    while (scanf("%s",str)!=EOF)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        long long sum=0;
        int i;
        for (i=0;str[i]!='\0';i++)
        {
            if (str[i]>='0'&& str[i]<='9')
               sum=sum*a+str[i]-'0';
            else
               sum=sum*a+str[i]-'A'+10;
        }
        int len=0;
        int num[30];
        do {
            num[len++]=sum%b;
            sum/=b;
        } while(sum);
        if (len>7)
        {
            printf("  ERROR\n");
        }
        else
        {
            for (i=0;i<7-len;i++)
                printf(" ");
            for (i=len-1;i>=0;i--)
               if (num[i]>9)
                  printf("%c",num[i]-10+'A');
               else
                  printf("%d",num[i]);
            printf("\n");
        }
    }
    return 0;
}

         將上面的源程式提交給“http://acm.hdu.edu.cn/showproblem.php?pid=1335 Basically Speaking”，可以Accepted。

【例5】數位和統計

問題描述

給出2個b進位正整數s和t，算出s和t間所有整數的數位之和。數位和的意思是一個數各個位置上的和。例如，十進位數1357的數位和是16（=1+3+5+7）；十六進位數9A8C的數位和是39（=9+10+8+12）。

輸入

第一行一個整數b表示進位，2<=b<=36，A代表10，B代表11，...，Z代表35，以此類推

第二行兩個b進位正整數s和t，s、t在10進位下小於1000000。

輸出

一個十進位整數表示s和t間所有整數的數位之和

輸入樣例

11

A 1A

輸出樣例

76

        （1）編程思路。

        先將b進位數s和t轉換為十進位整數，再用迴圈對s至t之間所有的整數求每個整數在b進位下的各位數字之和，並將這些求得的和累加起來。

        （2）源程式。

#include <stdio.h>
int digitSum(int n,int b)  // 求10進位整數n對應B進位數的各位數字和
{
    int s=0;
    while (n!=0)
    {
        s+=n%b;
        n/=b;
    }
    return s;
}
int change(char s[],int b)  // 將b進位數轉換為10進位數
{
    int i,num,sum=0;
    for (i=0; s[i]!='\0';i++)
    {
        num=s[i]-'0';
        if (num>9) num-=7;
        sum=sum*b+num;
    }
    return sum;
}
int main()
{
    int b;
    scanf("%d",&b);
    char s[21],t[21];
    scanf("%s %s",s,t);
    int i,x,y;
    x=change(s,b);
    y=change(t,b);
    if (x>y)
    {
        int temp;
        temp=x; x=y; y=temp;
    }
    int sum=0;
    for (i=x; i<=y;i++)
        sum+=digitSum(i,b);
    printf("%d\n",sum);
    return 0;
}

【例6】失戀的小W

問題描述

小W在3月7日這天失戀了，傷心的他開始無比討厭3和7這兩個數字，於是他創造了W計數法。W計數法在十進位的基礎上去掉了所有含有數字3和數字7的數，例如2的下一個數是4,29的下一個數是40。小W想知道在這種計數法下X到Y之間有多少個數。

輸入

一行兩個整數表示X、Y，保證1<=X<=Y<=10^9，保證X和Y中不含數字3和數字7。

輸出

一行一個整數表示X到Y之間有多少個數。

輸入樣例

10 100

輸出樣例

57

        （1）編程思路。

       所謂的W計數法就是八進位數。在W計數法中，有0,1,2,4,5,6,8,9等八個數位，規則同樣“逢八進一”，只不過W計數法中的“8”相當於十進位數中的“6”，W計數法中的“9”相當於十進位數中的“7”。若給出一個十進位數，要轉換為W計數法中的數，則十進位的4、5、6應分別轉換成3、4、5，8和9要轉換為6和7。也就是說，將十進位整數轉換成W計數法表示的八進位數時，每位的數字轉換為一個數字，若數字超過了7，則減去2；若數字在4~6之間，則減去1；若數字為0~2，則保持不變。W計數法中不存在3和7。

    按上面的方法將十進位數X寫成W計數法表示的八進位數後，再將這個八進位數轉換成十進位數，就知道W計數法中，X是第幾個數。同樣，將十進位數Y寫成W計數法表示的八進位數後，再將這個八進位數轉換成十進位數，就知道W計數法中，Y是第幾個數。這樣就知道X到Y之間有多少個數了。

        （2）源程式。

#include <stdio.h>
void dec2w(int n,char s[])  // 將10進位整數n轉換為w計數法對應的八進位數，並保存到字元串s中
{
    int i,j,k=0;
    int a[13];
    while (n!=0)
    {
        a[k]=n%10;
        if (a[k]>=7)
            a[k]=a[k]-2;
        else if(a[k]>=3)
            a[k]--;
        n=n/10;
        k++;
    }
    for (i=k-1,j=0;i>=0;i--,j++)
        s[j]=a[i]+'0';
    s[j]='\0';
}
int oct2dec(char s[])  // 將s中保存的8進位數轉換為10進位數並返回
{
    int i,sum=0;
    for (i=0; s[i]!='\0';i++)
    {
        sum=sum*8+s[i]-'0';
    }
    return sum;
}
int main()
{
    int x,y;
    scanf("%d %d",&x,&y);
    char s[13];
    dec2w(x,s);
    x=oct2dec(s);
    dec2w(y,s);
    y=oct2dec(s);
    printf("%d\n",y-x+1);
    return 0;
}

【例7】Base B

問題描述

小紅非常喜歡數學。他喜歡研究數字。他知道如何將非負整數表示為基數為P的數字。比如，他知道71的基數為2的數字表示是“1000111”，65的基數為5的數字表示是“230”。但小紅希望創建一種所謂“Base B”的數字表達方式。在該表達方式中，其每個數字值不僅等於或大於A，還小於A+B。例如，如果A=1，B=5，那麼在“Base 5”中表示數字65，它肯定是“225”，不會是“230”（0超出範圍[1,5]）。

225=2*52+2*51+5*50=50+10+5=65

小紅對這種表示法非常感興趣，現在他希望你能為他編寫一個程式，幫助他在“Base B”中表示一個數字N。

輸入

輸入由多組測試用例組成。每組測試用例占1行，每行有三個整數表示N、A、B（0<=N<=10^9、0<=A<=100、2<=B<=100）。

輸出

對於每組測試用例，輸出N在“Base B”中的表示方式，各數字之間用空格分隔。

輸入樣例

65 1 5

15 0 2

輸出樣例

Case 1: 2 2 5

Case 2: 1 1 1 1

        （1）編程思路。

        先將輸入的十進位整數N轉換為b進位數。由於“Base B”中要求每位上的數不能小於a。因此，需要進行校正。校正方法為：將轉換後得到的b進位數從低位到高位進行處理。如果當前位上數小於a，則從高一位借1，然後當前位加b。

        （2）源程式。

#include <stdio.h>
int main()
{
    int n,a,b,iCase=0;
    while (scanf("%d%d%d",&n,&a,&b)!=EOF)
    {
        int cnt=0;
        int digit[32];
        while (n)              // 將n轉換為b進位保存在數組digit中
        {
            digit[cnt++]=n%b;
            n/=b;
        }
        int i;
        for (i=0;i<cnt-1;i++)  // 對小於a的數字進行校正
        {
            while (digit[i]<a)
            {
                digit[i]+=b;
                digit[i+1]--;
            }
        }
        printf("Case %d:",++iCase);
        for (i=cnt-1;i>=0;i--)
        {
            printf(" %d",digit[i]);
        }
        printf("\n");
    }
    return 0;
}

        將上面的源程式提交給http://acm.hdu.edu.cn/showproblem.php?pid=2864 “Base B”，可以Accepted。

【例8】約數的和

問題描述

給定一個十進位整數n，計算n的所有約數在m進位中各位數字的平方和。

例如，給定整數n=10，它的約數有1, 2, 5, 10，表示為2進位數為1, 10, 101, 1010。在2進位中，這些約數的各位數字的平方和為

1^2+ (1^2 + 0^2) + (1^2 + 0^2 + 1^2) + .... = 6 = 110（表示為2進位數）。

輸入

輸入包括多個測試用例，每個測試用例是一行，包括兩個十進位整數n和m（1≤n≤109，2≤m≤16）。

輸出

所有約數在m進位中各位數字的平方和。

輸入樣例

10 2

30 5

輸出樣例

110

112

        （1）編程思路。

         先用迴圈求出n的所有約數並保存到數組a中。再求每個約數在m進位下的各位數字的平方和，並將求得的平方和累加起來。最後將求得的和值（十進位數）轉換為m進位數輸出。

        （2）源程式。

#include <stdio.h>
#include <math.h>
int main()
{
    int n, m;
    while (scanf("%d%d",&n,&m)!=EOF)
    {
        int i,temp = sqrt(n);
        int cnt = 0;
        int a[10005];
        for (i = 1;i<=temp;i++)   // 求出n的所有因數並保存到數組a中
        {
            if (n%i == 0)
            {
                a[cnt++] = i;
                if (i!= n/i) a[cnt++] = n / i;
            }
        }
        int sum = 0;
        for (i = 0;i < cnt;i++) // 求出n的所有因數在m進位下的各位數字的平方和
        {
            temp = a[i];
            while (temp)
            {
                sum += (temp%m)*(temp%m);
                temp /= m;
            }
        }
        char ans[32];
        cnt = 0;
        while (sum)            // 將求得的和值（十進位數）轉換為m進位數輸出
        {
            temp = sum%m;
            if (temp < 10)
                ans[cnt++] = temp + '0';
            else
                ans[cnt++] = temp - 10 + 'A';
            sum /= m;
        }
        for (i = cnt - 1;i >= 0;i--)
            printf("%c",ans[i]);
        printf("\n");
    }
    return 0;
}

      將上面的源程式提交給 http://acm.hdu.edu.cn/showproblem.php?pid=4432  Sum of divisors，可以Accepted。


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 前端JavaScript初學者提升前端技能必須要練習的15個項目推薦，趕快收藏！！！
    要成為一名優秀的 Web 開發人員，最快的方法就是練習。一個很好的練習方法是儘可能多地構建初學者項目。那是因為每個項目都會提出一個獨特的問題和解決方案，因此您解決的項目越多，您獲得的知識就越多。將您完成的每個項目都視為您獲得的獎牌。您擁有的獎牌越多，您就越能準備好應對下一個難度更大的項目。 為了幫助 ...
  • 情侶紀念日網站html5源碼教程
    個人名片： 對人間的熱愛與歌頌，可抵歲月冗長:sun_with_face: Github👨🏻‍💻：念舒_C.ying CSDN主頁✏️：念舒_C.ying 個人博客:earth_asia: ：念舒_C.ying 預覽圖 直接進入我的網站吧 >> Z_C戀愛日記 下載源碼 鏈接：https:// ...
  • VUE3 自定義 輕量級全局數據共用方案之一 Provide&inject （簡單快速實現vuex功能）
    在vue2中，提供了provide和inject配置，可以讓開發者在高層組件中註入數據，然後在後代組件中使用 除了相容vue2的配置式註入，vue3在composition api 中添加了provide和inject方法，可以在setup函數中註入 和使用數據 基本使用 provide('key' ...
  • VUE3 全局共用數據方案之一 global state （簡單快速實現類似vuex）
    自定義 封裝單列模式！ global state 由於vue3的響應式系統本身可以脫離組件而存在，因此可以充分利用這一點，輕鬆製造多個全局響應式數據， 並且通過和vuex一樣 通過某個模塊指定方法修改數據，不能直接修改數據，並且讓數據成為全局響應式 並且在代碼體積上絕對的輕量級！比市面上的任何第三方 ...
  • 在Spring Security中如何獲取AuthenticationManager對象？
    一.小結 1.程式模塊化和可重用性是軟體工程的中心目標之一。java提供了很多有助於完成這一目標的有效結構。方法就是一個這樣的結構。 2.方法指定方法的修飾符，返回值類型，方法名和參數。比如靜態修飾符static。 3.方法可以返回一個值。返回值類型returnValueType是方法要返回的值數據 ...
  • day23-伺服器端渲染技術01
    伺服器端渲染技術01 為什麼需要jsp？ 在之前的開發過程中，我們可以發現servlet做界面非常不方便： 引出jsp技術=> jsp=html+java代碼+標簽+javascript+css 1.JSP基本介紹 JSP全稱是Java Server Pages，Java的伺服器頁面，就是伺服器端渲 ...
  • OpenGL 褐色
    目錄 一.OpenGL 褐色 1.IOS Object-C 版本 1.Windows OpenGL ES 版本 2.Windows OpenGL 版本 二.OpenGL 褐色 GLSL Shader 三.猜你喜歡 零基礎 OpenGL ES 學習路線推薦 : OpenGL ES 學習目錄 >> Op ...
  • Java——多線程：Lamda表達式
    多線程理解 繼承Thread類 子類繼承Thread類具備多線程能力 啟動線程：子類對象.start() 不建議使用：避免oop單繼承局限性 實現Runnable介面 實現介面Runnable具有多線程能力 啟動線程：傳入目標對象+Thread對象.start() 推薦使用：避免單繼承局限性，可能一 ...
一周排行
    -Advertisement-
    Play Games
  • Dapr Outbox 執行流程
    Dapr Outbox 是1.12中的功能。 本文只介紹Dapr Outbox 執行流程，Dapr Outbox基本用法請閱讀官方文檔 。本文中appID=order-processor，topic=orders 本文前提知識：熟悉Dapr狀態管理、Dapr發佈訂閱和Outbox 模式。 Outbo ...
  • Advanced .Net Debugging 7：托管堆與垃圾收集
    引言 在前幾章我們深度講解了單元測試和集成測試的基礎知識，這一章我們來講解一下代碼覆蓋率,代碼覆蓋率是單元測試運行的度量值,覆蓋率通常以百分比表示，用於衡量代碼被測試覆蓋的程度，幫助開發人員評估測試用例的質量和代碼的健壯性。常見的覆蓋率包括語句覆蓋率（Line Coverage）、分支覆蓋率（Bra ...
  • C#S7.NET實現西門子PLCDB塊數據採集的完整步驟
    前言 本文介紹瞭如何使用S7.NET庫實現對西門子PLC DB塊數據的讀寫，記錄了使用電腦模擬，模擬PLC，自至完成測試的詳細流程，並重點介紹了在這個過程中的易錯點，供參考。 用到的軟體： 1.Windows環境下鏈路層網路訪問的行業標準工具（WinPcap_4_1_3.exe）下載鏈接：http ...
  • WPF控制項：密碼框綁定MVVM
    從依賴倒置原則（Dependency Inversion Principle, DIP）到控制反轉（Inversion of Control, IoC）再到依賴註入（Dependency Injection, DI）的演進過程，我們可以理解為一種逐步抽象和解耦的設計思想。這種思想在C#等面向對象的編 ...
  • Python中的私有屬性與私有方法
    關於Python中的私有屬性和私有方法 Python對於類的成員沒有嚴格的訪問控制限制，這與其他面相對對象語言有區別。關於私有屬性和私有方法，有如下要點： 1、通常我們約定，兩個下劃線開頭的屬性是私有的（private）。其他為公共的（public）； 2、類內部可以訪問私有屬性（方法）； 3、類外 ...
  • C++ 訪問說明符詳解：封裝數據，控制訪問，提升安全性
    C++ 訪問說明符 訪問說明符是 C++ 中控制類成員（屬性和方法）可訪問性的關鍵字。它們用於封裝類數據並保護其免受意外修改或濫用。 三種訪問說明符： public：允許從類外部的任何地方訪問成員。 private：僅允許在類內部訪問成員。 protected：允許在類內部及其派生類中訪問成員。 示 ...
  • static_cast與dynamic_cast到底是什麼？
    寫這個隨筆說一下C++的static_cast和dynamic_cast用在子類與父類的指針轉換時的一些事宜。首先，【static_cast，dynamic_cast】【父類指針，子類指針】，兩兩一組，共有4種組合：用 static_cast 父類轉子類、用 static_cast 子類轉父類、使用 ...
  • C語言數據結構：雙向鏈表的增刪操作
    /******************************************************************************************************** * * * 設計雙向鏈表的介面 * * * * Copyright (c) 2023-2 ...
  • @ComponentScan註解的實現，Spring掃描包的過程
    相信接觸過spring做開發的小伙伴們一定使用過@ComponentScan註解 @ComponentScan("com.wangm.lifecycle") public class AppConfig { } @ComponentScan指定basePackage，將包下的類按照一定規則註冊成Be ...
  • opensips開啟python支持
    操作系統 ：CentOS 7.6_x64 opensips版本： 2.4.9 python版本：2.7.5 python作為腳本語言，使用起來很方便，查了下opensips的文檔，支持使用python腳本寫邏輯代碼。今天整理下CentOS7環境下opensips2.4.9的python模塊筆記及使用 ...
所有分類