在說神經網路之前,我們討論一下神經元(Neurons),它是神經網路的基本單元。神經元先獲得輸入,然後執行某些數學運算 後,再產生一個輸出。比如一個2輸入神經元的例子: 在這個神經元里,輸入總共經歷了3步數學運算,先將輸入乘以權重(weight): 最後經過激活函數(activation funct ...
在說神經網路之前,我們討論一下神經元(Neurons),它是神經網路的基本單元。神經元先獲得輸入,然後執行某些數學運算
後,再產生一個輸出。比如一個2輸入神經元的例子:
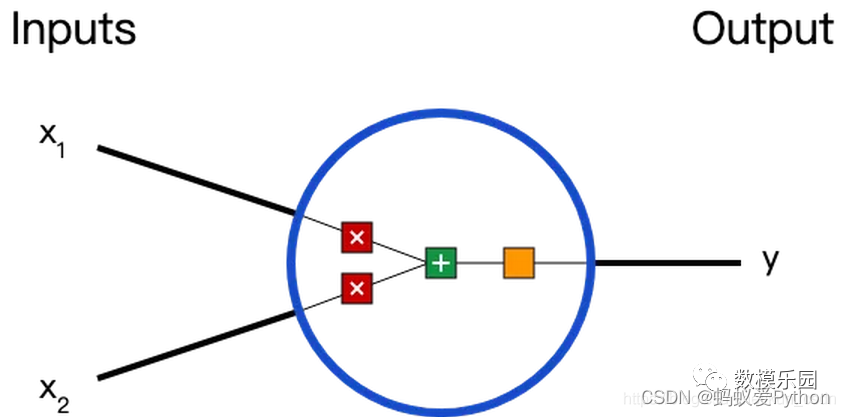
在這個神經元里,輸入總共經歷了3步數學運算,先將輸入乘以權重(weight):
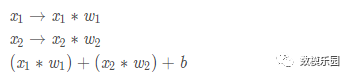
最後經過激活函數(activation function)處理得到輸出:
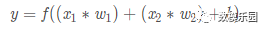
激活函數的作用是將無限制的輸入轉換為可預測形式的輸出。一種常用的激活函數是sigmoid函數:
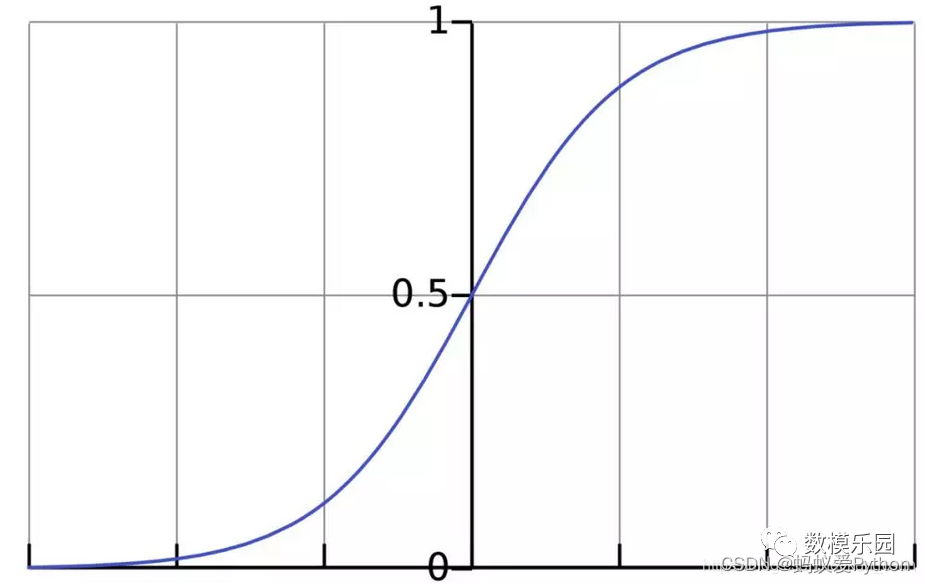
sigmoid函數的輸出介於0和1,我們可以理解為它把 (−∞,+∞) 範圍內的數壓縮到 (0, 1)以內。正值越大輸出越接近1,負向數值越
大輸出越接近0。舉個例子,上面神經元里的權重和偏置取如下數值:


以上步驟的Python代碼是:
Python學習交流Q群:906715085### import numpy as np def sigmoid(x): # our activation function: f(x) = 1 / (1 * e^(-x)) return 1 / (1 + np.exp(-x)) class Neuron(): def __init__(self, weights, bias): self.weights = weights self.bias = bias def feedforward(self, inputs): # weight inputs, add bias, then use the activation function total = np.dot(self.weights, inputs) + self.bias return sigmoid(total) weights = np.array([0, 1]) # w1 = 0, w2 = 1 bias = 4 n = Neuron(weights, bias) # inputs x = np.array([2, 3]) # x1 = 2, x2 = 3 print(n.feedforward(x)) # 0.9990889488055994
搭建神經網路
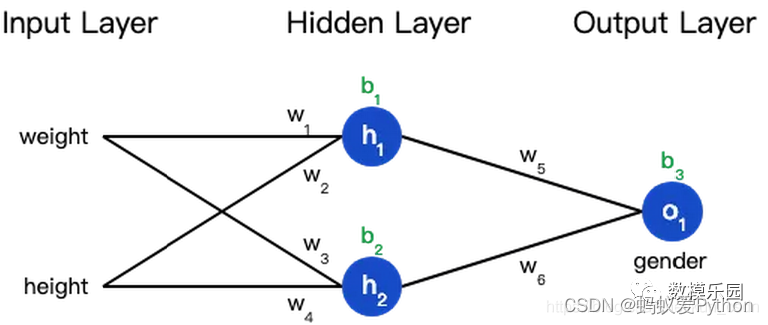
神經網路就是把一堆神經元連接在一起,下麵是一個神經網路的簡單舉例:
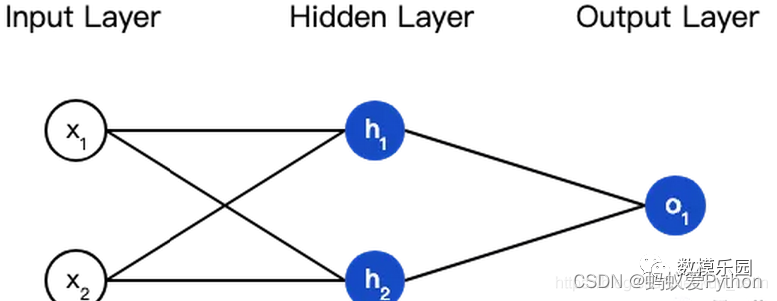
這個網路有2個輸入、一個包含2個神經元的隱藏層(h1和h2)、包含1個神經元的輸出層o1。
隱藏層是夾在輸入輸入層和輸出層之間的部分,一個神經網路可以有多個隱藏層。
把神經元的輸入向前傳遞獲得輸出的過程稱為前饋(feedforward)。
我們假設上面的網路里所有神經元都具有相同的權重w = [ 0 , 1 ]]和偏置b = 0 ,激活函數都是 sigmoid,那麼我們會得到什麼輸出呢?
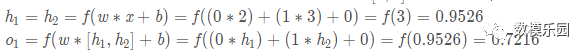
以下是實現代碼:
Python學習交流Q群:906715085### class OurNeuralNetworks(): """ A neural network with: - 2 inputs - a hidden layer with 2 neurons (h1, h2) - an output layer with 1 neuron (o1) Each neural has the same weights and bias: - w = [0, 1] - b = 0 """ def __init__(self): weights = np.array([0, 1]) bias = 0 # The Neuron class here is from the previous section self.h1 = Neuron(weights, bias) self.h2 = Neuron(weights, bias) self.o1 = Neuron(weights, bias) def feedforward(self, x): out_h1 = self.h1.feedforward(x) out_h2 = self.h2.feedforward(x) # The inputs for o1 are the outputs from h1 and h2 out_o1 = self.o1.feedforward(np.array([out_h1, out_h2])) return out_o1 network = OurNeuralNetworks() x = np.array([2, 3]) print(network.feedforward(x)) # 0.7216325609518421

訓練神經網路
現在我們已經學會瞭如何搭建神經網路,現在再來學習如何訓練它,其實這是一個優化的過程。假設有一個數據集,包含4個人的
身高、體重和性別:
Name Weight (lb) Height (in) Gender Alice 133 65 F Bob 160 72 M Charlie 152 70 M Diana 120 60 F
現在我們的目標是訓練一個網路,根據體重和身高來推測某人的性別。
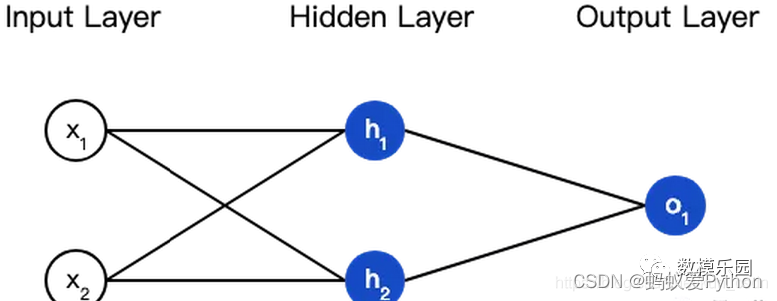
為了簡便起見,我們將每個人的身高、體重減去一個固定數值,把性別男定義為1、性別女定義為0。
Name Weight (減去135) Height (減去66) Gender Alice -2 -1 0 Bob 25 6 1 Charlie 17 4 1 Diana -15 -6 0
在訓練神經網路之前,我們需要有一個標准定義它到底好不好,以便我們進行改進,這就是損失(loss)。
顧名思義,均方誤差就是所有數據方差的平均值,我們不妨就把它定義為損失函數。預測結果越好,損失就越低,訓練神經網路
就是將損失最小化。
如果上面網路的輸出一直是0,也就是預測所有人都是男性,那麼損失是
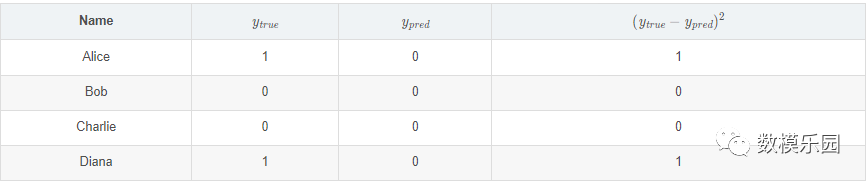
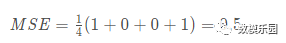
Python學習交流Q群:906715085### def mse_loss(y_true, y_pred): # y_true and y_pred are numpy arrays of the same length return ((y_true - y_pred) ** 2).mean() y_true = np.array([1, 0, 0, 1]) y_pred = np.array([0, 0, 0, 0]) print(mse_loss(y_true, y_pred)) # 0.5

減少神經網路損失
這個神經網路不夠好,還要不斷優化,儘量減少損失。我們知道,改變網路的權重和偏置可以影響預測值,但我們應該怎麼做
呢?為了簡單起見,我們把數據集縮減到只包含Alice一個人的數據。於是損失函數就剩下Alice一個人的方差:
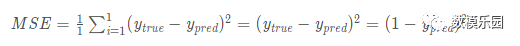
預測值是由一系列網路權重和偏置計算出來的:
所以損失函數實際上是包含多個權重、偏置的多元函數:


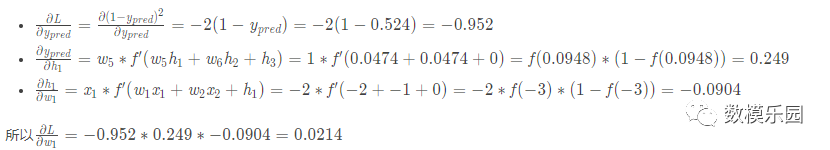
這個結果告訴我們:如果增大w1,損失函數L會有一個非常小的增長。

隨機梯度下降
下麵將使用一種稱為隨機梯度下降(SGD)的優化演算法,來訓練網路。經過前面的運算,我們已經有了訓練神經網路所有數據。
但是該如何操作?SGD定義了改變權重和偏置的方法:

從數據集中選擇一個樣本;
計算損失函數對所有權重和偏置的偏導數;
使用更新公式更新每個權重和偏置;
回到第1步。
隨著學習過程的進行,損失函數逐漸減小。
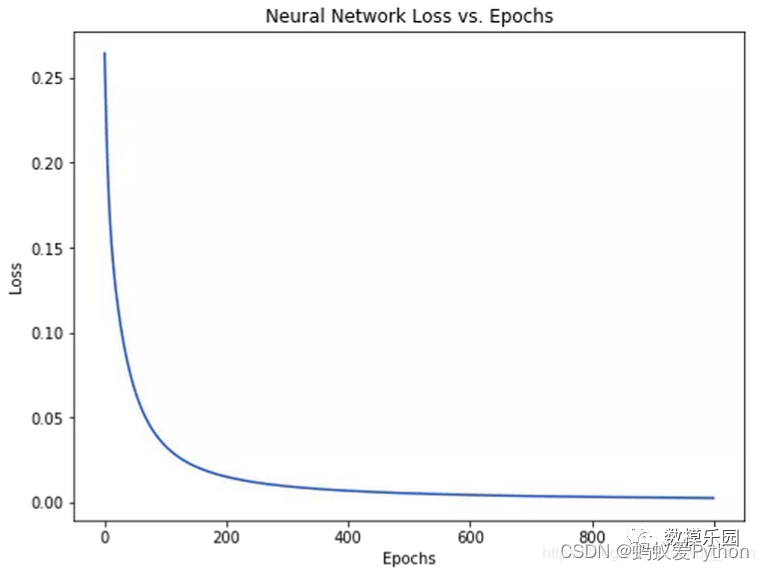
現在我們可以用它來推測出每個人的性別了:
# Make some predictions emily = np.array([-7, -3]) # 128 pounds, 63 inches frank = np.array([20, 2]) # 155 pounds, 68 inches print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - F print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M
最後
今天的案例到這裡就結束了,喜歡的小伙伴可以點贊收藏加關註,有問題的小伙伴可以評論告訴我。然後,下一章見啦!!!



