樹 定義 樹是遞歸定義的。 一棵樹是由n(n>0)個元素組成的有限集合,其中每個元素稱為結點(node),有一個特定的結點,稱為樹根(root),除根結點外,其餘結點能分成m(m>=0)個互不相交的有限集合T0,T1,T2,……Tm-1,其中的每個子集又都是一棵樹,這些集合稱為這棵樹的子樹。 如圖是 ...
樹
定義
樹是遞歸定義的。
一棵樹是由n(n>0)個元素組成的有限集合,其中每個元素稱為結點(node),有一個特定的結點,稱為樹根(root),除根結點外,其餘結點能分成m(m>=0)個互不相交的有限集合T0,T1,T2,……Tm-1,其中的每個子集又都是一棵樹,這些集合稱為這棵樹的子樹。
如圖是一棵樹:
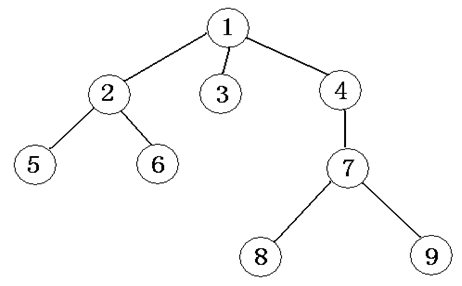
一棵樹中至少有1個結點,即根結點。
一個結點的子樹個數,稱為這個結點的度(如結點1的度為3,結點3的度為0)。
度為0的結點稱為葉結點(leaf)(如結點3、5、6、8、9)。
樹中各結點的度的最大值稱為這棵樹的度(此樹的度為3)。
上端結點為下端結點的父結點,稱同一個父結點的多個子結點為兄弟結點(如結點1是結點2、3、4的父結點,結點 2、3、4是結點1的子結點,它們又是兄弟結點)。
遍歷
樹結構解決問題時,按照某種次序獲得樹中全部結點的信息,這種操作叫作樹的遍歷。
先序(根)遍歷
先訪問根結點,再從左到右按照先序思想遍歷各棵子樹(如,上圖先序遍歷的結果為125634789)。
後序(根)遍歷
先從左到右遍歷各棵子樹,再訪問根結點(如,上圖後序遍歷的結果為562389741)。
層次遍歷
按層次從小到大逐個訪問,同一層次按照從左到右的次序(如,上圖層次遍歷的結果為123456789)。
葉結點遍歷
即從左到右遍歷所有葉節點(如,上圖葉節點遍歷的結果為56389)。
二叉樹
二叉樹是一種特殊的樹型結構,它是度數為2的樹,即二叉樹的每個結點最多有兩個子結點。
每個結點的子結點分別稱為左兒子、右兒子。
五種基本形態
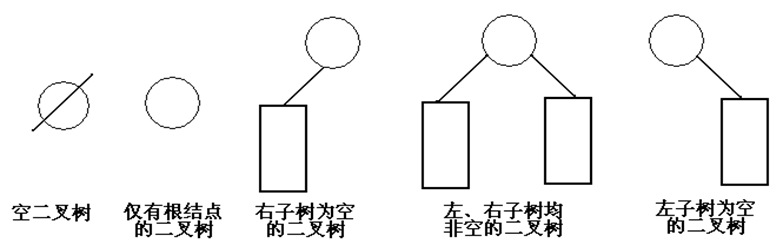
性質
性質一
二叉樹的第i層最多有2i-1個結點(i>=1)(可用二進位性質解釋。)。
性質二
深度為k的二叉樹至多有2k–1個結點(k>=1)。
性質三
任意一棵二叉樹,如果其葉結點數為n0,度為2的結點數為n2,則一定滿足:n0=n2+1。
性質四
有n個結點的完全二叉樹的深度為floor(log2n)+1。
性質五
一棵n個結點的完全二叉樹,對任一個結點(編號為i),有:如果i=1,則結點i為根,無父結點;如果i>1,則其父結點編號為floor(i/2),如果i為父節點編號,那麼2*i是左孩子,2*i+1是右孩子。
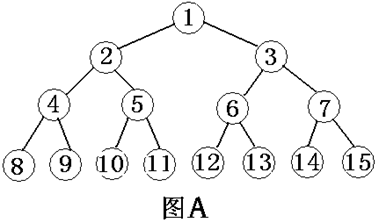
圖A-滿二叉樹
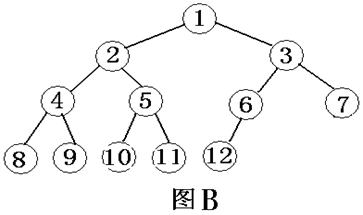
圖B-完全二叉樹
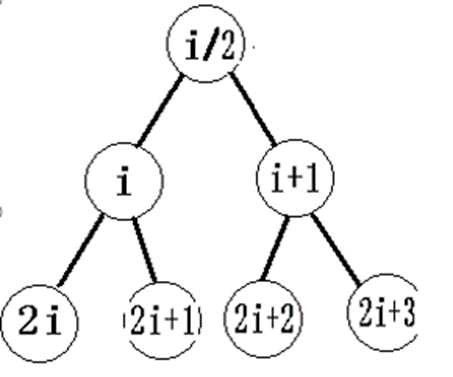
編號示意圖
遍歷
二叉樹的遍歷是指按一定的規律和次序訪問樹中的各個結點。
遍歷一般按照從左到右的順序,共有3種遍歷方法,先(根)序遍歷,中(根)序遍歷,後(根)序遍歷。
先序遍歷
若二叉樹為空,則空操作,否則:
訪問根結點、先序遍歷左子樹、先序遍歷右子樹
void preorder(tree bt)//先序遞歸演算法
{
if(bt)
{
cout << bt->data;
preorder(bt->lchild);
preorder(bt->rchild);
}
}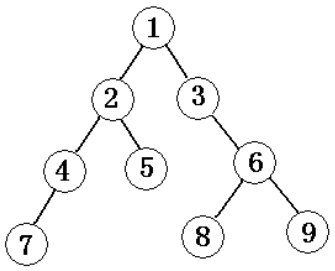
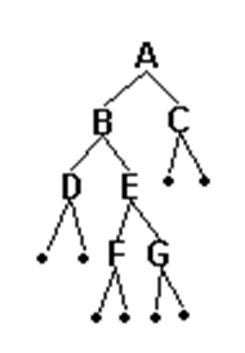
先序遍歷此圖結果為:124753689
中序遍歷
若二叉樹為空,則空操作,否則:
中序遍歷左子樹、訪問根結點、中序遍歷右子樹
void inorder(tree bt)//中序遍歷遞歸演算法
{
if(bt)
{
inorder(bt->lchild);
cout << bt->data;
inorder(bt->rchild);
}
}中序遍歷上圖結果為:742513869
後序遍歷
若二叉樹為空,則空操作,否則:
後序遍歷左子樹、後序遍歷右子樹、訪問根結點
void postorder(tree bt)//後序遞歸演算法
{
if(bt)
{
postorder(bt->lchild);
postorder(bt->rchild);
cout << bt->data;
}
}後序遍歷上圖結果為:745289631
已知先序序列和中序序列可唯一確定一棵二叉樹;
已知中序序列和後序序列可唯一確定一棵二叉樹;
已知先序序列和後序序列不可唯一確定一棵二叉樹;
二叉樹操作(建樹、刪除、輸出)
普通樹轉二叉樹
由於二叉樹是有序的,而且操作和應用更廣泛,所以在實際使用時,我們經常把普通樹轉換成二叉樹進行操作。
通用法則:“左孩子,右兄弟”
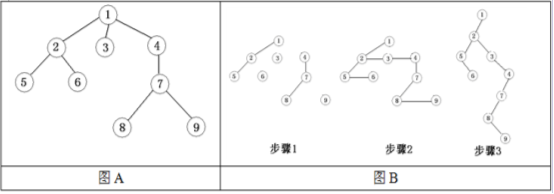
建樹

刪除樹
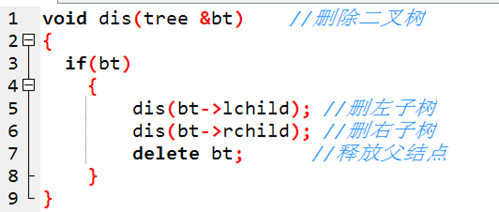
插入一個結點到排序二叉樹中

在排序二叉樹中查找一個數

相關題目
擴展二叉樹
由於先序、中序和後序序列中的任一個都不能唯一確定一棵二叉樹,所以對二叉樹做如下處理,將二叉樹的空結點用“.”補齊,稱為原二叉樹的擴展二叉樹,擴展二叉樹的先序和後序序列能唯一確定其二叉樹。
現給出擴展二叉樹的先序序列,要求輸出其中序和後序序列。
輸入樣例:
ABD..EF..G..C..
輸出樣例:
DBFEGAC
DFGEBCA


二叉樹的建立和輸出
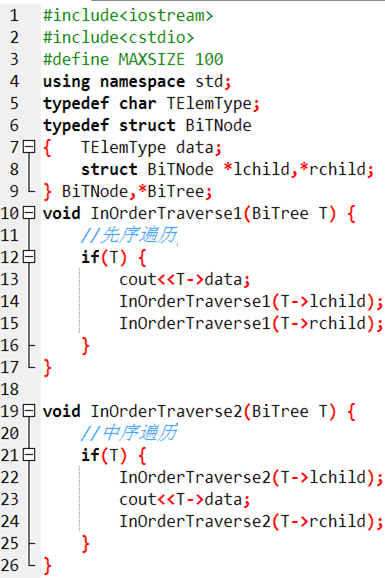
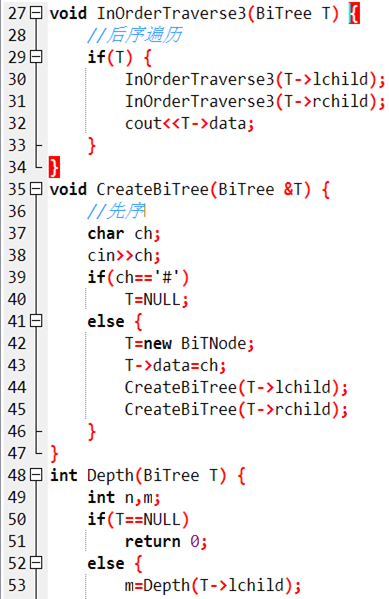
以二叉鏈表作存儲結構,建立一棵二叉樹,並輸出該二叉樹的先序、中序、後序遍歷序列、高度和結點總數。
輸入樣例:
12##3##
//#為空
輸出樣例:
123
//先序排列
213
//中序排列
231
//後序排列
2
//高度
3
//結點總數

因為本蒟蒻不太會用指針,所以自己寫了一個不帶指針的,代碼很醜,見諒QwQ
#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
int top,maxh;
char s;
struct t{
int data,father,lson=0,rson=0,h=0;
}tree[100005];
void build(int father,bool right){
cin>>s;
if(s=='\n')
return;
if(s!='#'){
++top;
int t=top;
tree[t].father=father;
tree[t].data=s-'0';
tree[t].h=tree[father].h+1;
maxh=max(tree[t].h,maxh);
if(right==1)
tree[father].rson=t;
else
tree[father].lson=t;
build(t,0);
build(t,1);
}
else return;
}
void xian(int now){
cout<<tree[now].data;
if(tree[now].lson!=0)
xian(tree[now].lson);
if(tree[now].rson!=0)
xian(tree[now].rson);
}
void zhong(int now){
if(tree[now].lson!=0)
zhong(tree[now].lson);
cout<<tree[now].data;
if(tree[now].rson!=0)
zhong(tree[now].rson);
}
void hou(int now){
if(tree[now].lson!=0)
hou(tree[now].lson);
if(tree[now].rson!=0)
hou(tree[now].rson);
cout<<tree[now].data;
}
int main(){
build(0,0);
// for(int i=1;i<=top;i++){
// cout<<tree[i].data<<' '<<tree[i].father<<' ';
// cout<<tree[i].lson<<' '<<tree[i].rson<<' ';
// cout<<tree[i].h<<endl;;
// }
xian(1);
cout<<'\n';
zhong(1);
cout<<'\n';
hou(1);
cout<<'\n';
cout<<maxh<<'\n'<<top<<'\n';
return 0;
}P1030 求先序排列
給出一棵二叉樹的中序與後序排列。求出它的先序排列。(約定樹結點用不同的大寫字母表示,長度<=8)。
輸入:
2行,均為大寫字母組成的字元串,表示一棵二叉樹的中序與 後序排列。
輸出:
1行,表示一棵二叉樹的先序。
輸入樣例:
BADC
BDCA
輸出樣例:
ABCD
分析
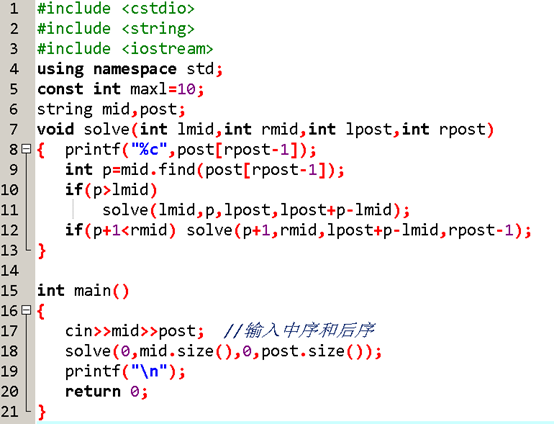
中序為BADC,後序為BDCA,所以A為根結點,B、DC分別為左右子樹的中序序列,B、DC分別為左右子樹的後序序列。然後再遞歸處理中序為B,後序為B的子樹和中序為DC,後序為DC的子樹。
自己用char數組寫的代碼QwQ
#include<iostream>
#include<cstring>
#include<cstdio>
#define ll long long
using namespace std;
char mid[10],post[10];
//mid數組記錄中序排列,post數組記錄後序排列
//除了打暴力最好不要用string
int z[10],m[10],p[10];
//z數組做中轉使用,m數組記錄mid數組的內容,p數組記錄post數組的每一位在mid數組中的位置
void find(int start,int end,int kai,int jie){
//start和end記錄我們正在找的mid數組的範圍
//kai(開頭)和jie(結尾)記錄我們正在找的post數組的範圍
if(start>end||kai>jie)return;
//如果開頭大於結尾,就返回
if(start==end||kai==jie){
printf("%c",mid[p[jie]]);
return;
}
//如果開頭等於結尾,那此節點一定沒有兒子,輸出當前節點並返回
printf("%c",mid[p[jie]]);
//前面說過後序排列的最後一位就是當前樹的根節點,所以p[jie]就是根節點在mid數組中的位置
//開頭小於結尾,那就輸出當前節點然後再去尋找此節點的左兒子和右兒子
find(start,p[jie]-1,kai,kai+p[jie]-start-1);
//求左子樹的範圍,然後遞歸尋找左兒子
find(p[jie]+1,end,kai+p[jie]-start,jie-1);
//求右子樹的範圍,然後遞歸尋找右兒子
}
int main(){
scanf("%s%s",mid+1,post+1);
//輸入時下標從1開始(主要是因為我比較毛病)
int len=strlen(mid+1);
//輸入時下標從1開始那麼計算字元串長度時也要加1
for(int i=1;i<=len;i++){
m[i]=mid[i]-'A'+1;
//將每一位轉成數字以方便處理(是的,我很毛病)
z[m[i]]=i;
//z數組記錄m數組每一位的位置(這一步是為了方便後面記錄post數字)
}
for(int i=1;i<=len;i++){
p[i]=z[post[i]-'A'+1];
//記錄post數組的每一位在mid數組中的位置
//z:我滴任務完成啦!
}
find(1,len,1,len);
//開始遞歸
return 0;
}求後序排列
輸入:
二叉樹的前序序列與中序序列
輸出:
二叉樹的後序序列
樣例輸入:
abcdefg
cbdafeg
樣例輸出:
cdbfgea
#include<iostream>
#include<cstring>
#include<cstdio>
#define ll long long
using namespace std;
char qian[100005],zhong[100005];
int q[100005],z[100005],a[100005],cnt=0;
void find(int start,int end){
if(start>end){
return;
}
cnt++;
if(start==end){
cout<<char(z[q[cnt]]+'a'-1);
return;
}
int t=cnt;
find(start,q[t]-1);
find(q[t]+1,end);
cout<<char(z[q[t]]+'a'-1);
}
int main(){
cin>>qian>>zhong;
int len=strlen(qian);
for(int i=0;i<len;i++){
a[zhong[i]-'a']=i;
}
for(int i=0;i<len;i++){
z[i+1]=zhong[i]-'a'+1;
q[i+1]=a[qian[i]-'a']+1;
}
find(1,strlen(qian));
return 0;
}因為有小可愛說我的代碼在輸入時的處理不清楚,所以又寫了一個版本QwQ
#include<iostream>
#include<cstring>
#include<cstdio>
#define ll long long
using namespace std;
char qian[100005],zhong[100005];
int q[100005],z[100005],a[100005],cnt=0;
void find(int start,int end){
// cout<<endl<<'*'<<start<<' '<<end<<'*'<<endl;
if(start>end){
return;
}
cnt++;
if(start==end){
cout<<char(z[q[cnt]]+'a'-1);
return;
}
int t=cnt;
find(start,q[t]-1);
find(q[t]+1,end);
cout<<char(z[q[t]]+'a'-1);
}
int main(){
// cin>>qian+1>>zhong+1;
scanf("%s%s",qian+1,zhong+1);//這裡的輸入下標從1開始
int len=strlen(qian+1);
for(int i=1;i<=len;i++){
a[zhong[i]-'a']=i;
}
for(int i=1;i<=len;i++){
z[i]=zhong[i]-'a'+1;
q[i]=a[qian[i]-'a'];
}
find(1,len);
return 0;
}補充
表達式樹
關於表達式樹,我們可以分別用先序、中序、後序的遍歷方法得出完全不同的遍歷結果,如,對於下圖的遍歷結果如下,它們對應著表達式的3種表示方法。
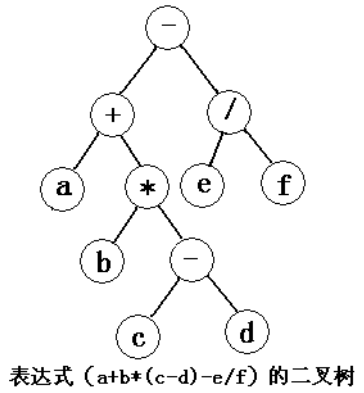
-+a*b-cd/ef (首碼表示、波蘭式)
a+b*(c-d)-e/f (中綴表示)
abcd-*+ef/- (尾碼表示、逆波蘭式)
哈夫曼樹
QwQ,不是很會,那就推薦一篇博客吧。
並非原創,僅是整理,請見諒
Lo問我為什麼看星星。我覺得銀河和代碼是同一種東西,這也是一種回答。————Co

