最小生成樹

下圖標明瞭六個城市（A~F）之間的公路（每條公路旁標註了其長度公裡數）。為將部分公路改造成高速公路，使各個城市之間均通過高速公路通達，至少要改造共計（）公裡的公路，這種總公裡數最少的改造方案共有（）個。

解析：

（1）普里姆演算法

任取一點，例如A，將其納入已完成部分。點A與其他各點中的最小距離為AE=200，從而將邊AE以及點E納入已完成部分，點A、E與其他各點B、C、D、F這兩個集合之間的最短距離為AF=AB=300，從而可以將邊AB與點B（或邊AF與點F）納入已完成部分。

點A、B、E與點C、D、F兩個集合的最短距離為AF=BF=300，從而可以將邊AF（或邊BF）與點F納入已完成部分。

點A、B、E、F與點C、D兩個集合之間的最短距離為FD=200，從而將邊FD與點D納入已完成部分。

點A、B、E、F、D與點C兩個集合之間的最短距離為CD=300，從而將邊CD與點C納入已完成部分。

此時，所有6個點都已經接通，其選為AE、AB、AF、FD、CD，總長度為1300。

（2）克魯斯卡爾演算法

依次選取長度最小的邊，題乾圖中是6個結點則需要5條邊（邊數=結點數-1），因此有：AE、FD為200，AB、BF、AF、CD為400，所以最終方案有3種。

最大流量

下圖標出了某地區的運輸網。各節點之間的運輸能力如下表（萬噸/小時），從節點1到節點6的最大運輸能力（流量）可以達到（）萬噸/小時。

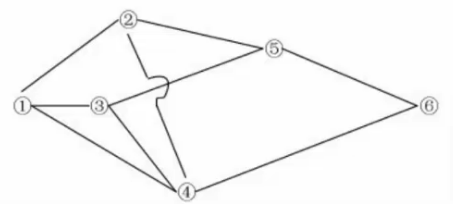
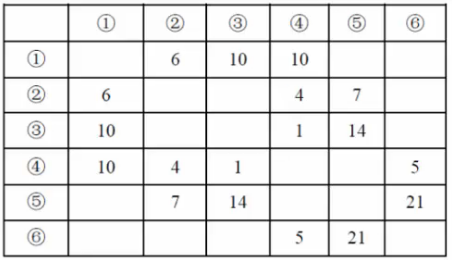
解析：

在本題中，從節點1到節點6可以同時沿多條路徑運輸，總的最大流量應是各條路徑上的最大流量之和，每條路徑上的最大流量應是其各段流量的最小值。解題時，每找出一條路徑算出流量後，該路徑上各段線路上的流量應扣除已經算過的流量，形成剩餘流量。剩餘流量為0的線段應將其刪除（斷開）。例如，路徑1、3、5、6的最大流量為10萬噸，計算後，該路徑上各段流量應都減少10萬噸。從而1、3之間斷開，3、5之間的剩餘流量是4萬噸，5、6之間的剩餘流量為11萬噸。

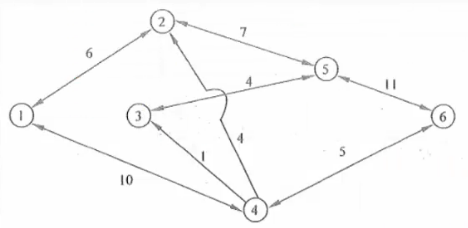
同理，依次執行類似步驟：

（1）路徑1、2、5、6的剩餘最大流量為6萬噸。計算過後，該路徑上各段流量應都減少6萬噸。從而1、2之間斷開，2、5之間的剩餘流量是1萬噸，5、6之間的剩餘流量為5萬噸。

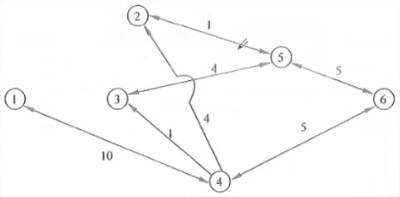
（2）路徑1、4、6的剩餘最大流量為5萬噸。計算過後，該路徑上各段流量應都減少5萬噸。從而4、6之間將斷開，1、4之間的剩餘流量是5萬噸。

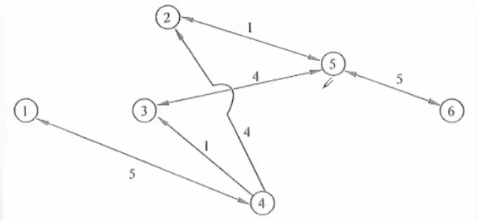
（3）路徑1、4、3、5、6的剩餘最大流量為1萬噸。計算過後，該路徑上各段流量應都減少1萬噸。從而4、3之間斷開，1、4之間的剩餘流量是4萬噸，3、5之間的剩餘流量是3萬噸，5、6之間的剩餘流量是4萬噸。

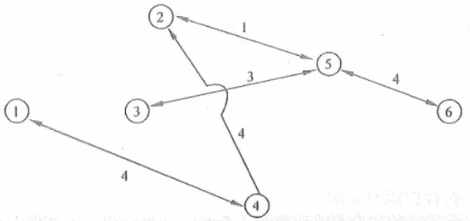
（4）路徑1、4、2、5、6的剩餘最大流量為1萬噸。計算後，該路徑上各段流量應減少1萬噸。從而2、5之間斷開，1、4之間，4、2之間，5、6之間的剩餘流量是3萬噸。

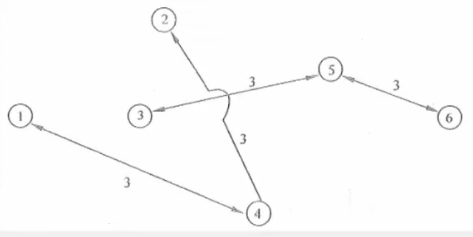
至此，從節點1到節點6已經沒有可通的路徑，因此，從節點1到節點6的最大流量應該是所有可能運輸路徑上的最大流量之和，即10+6+5+1+1=23萬噸。

決策論

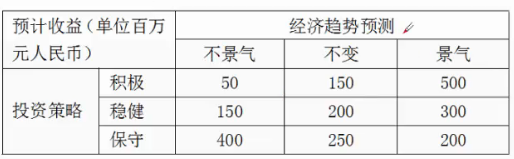
某公司需要根據下一年巨集觀經濟的增長趨勢預測決定投資策略。巨集觀經濟增長趨勢有不景氣、不變和景氣三種，投資策略有積極、穩健和保守三種，各種狀態收益如下表。

1、樂觀主義準則

樂觀主義準則，也稱為"最大最大準則"，其決策原則是"大中取大"。決策者依次在決策表中的各個投資方案所對應的各個結果中選擇出最大結果，並記錄，最後再從這些結果中選出最大者，其所對應的方案是應該採取的決策方案。

在本題中，積極方案的最大結果是500，穩健方案最大結果是300，保守方案最大結果是,400，三者最大值是500，選擇其對應的積極投資方案。

2、悲觀主義準則

悲觀主義準則也稱為"最大最小"原則，其決策原則是"小中取大"。決策者依次在決策表中各個投資方案所對應的各個結果中選出最小結果，並記錄，最後再從這些結果中選出最大者，其所對應的方案就是應該採取的方案。

例如本題，積極方案中最小結果是50，穩健方案最小結果是150，保守方案最小結果是200，三者的最大值是200，因此，選擇對應的保守投資方案。

3、後悔值準則

後悔值也叫做"最小最大後悔值"，該決策法的基本原理是，將每種自然狀態的最高值（指收益矩陣，如果是損失矩陣應取最低值）定為該狀態的理想目標，將該狀態中的其他值與最高值相比所得之差作為未達到理想的後悔值。為了提高決策的可靠性，在每一方案中選取最大的後悔值，再各方案的最大後悔值中選取最小值作為決策依據，與該值所對應的方案即為入選方案。

後悔值矩陣。

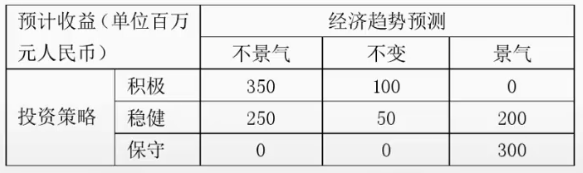
在表中，積極方案的最大後悔值為350，穩健方案的最大後悔值為250，保守方案的最大後悔值300。三者中的最小後悔值為250，因此，選擇其所對應的穩健投資方案。

靈敏度分析

假設有外表完全相同的木盒100只，將其分為2組，一組裝白球，有70盒；另一組裝黑球，有30盒。現在這100盒中任取一盒，請你猜，如果這盒內裝白球，猜對了得500分，猜錯了罰200分；如果這盒內裝黑球，猜對了得1000分，猜錯了罰150分。為使期望得分最多，應選哪一個方案？

解析：先畫出決策樹。

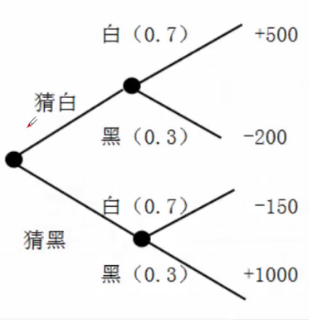
猜白球得分：0.7*500-0.3*200=290

猜黑球得分：0.3*1000-0.7*150=195

選擇猜白球。

但是當白球的概率從0.7變為0.6時，"猜白"的期望值是220，"猜黑"的期望值是310，此時，"猜黑"變成最優方案。概率的變化引起了最優方案的改變，這個轉折點的確定可以採用下麵的公式。

設P為出現白球的概率，1-P為出現黑球的概率。當兩個方案的期望值相等時，即：

P*500+(1-P)*(-200)=P*(-150)+(1-P)*1000，解出P=0.65，稱之為轉折率。

線性規劃

線性規劃最常考的是列方程，求解的問題。

某工廠計劃生產甲、乙兩種產品。生產每套產品所需的設備台時、A、 B兩種原料和可獲得利潤以及可利用資源數量，如表所示。則按（）方案來安排計劃以使該工廠獲利最多。

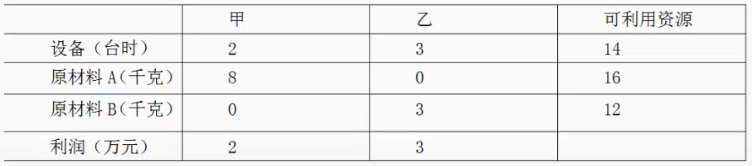
解析：設甲生產x套，乙生產y套，則：2x+3y<=14；x<=2；y<=4；同時滿足（2x+3y）最大，只有x=1，y=4，最大利潤14萬元。

動態規則

動態規則是一種將問題實例分解為更小的、相似的子問題，並存儲子問題的解而避免計算重覆的子問題，以解決最優化問題的演算法策略。

用一輛載重10噸的卡車裝運某倉庫中的貨物（不用考慮裝車時貨物的大小），這些貨物單件的重量和運算利潤如下。適當選擇裝運一些貨物若幹件，就能獲得最大總利潤（）元。

解析：若想獲得最高利潤最理想的方式是10噸都裝滿，且裝的貨物是單位利潤最高的那些貨物。因此，將每種貨物的單位利潤計算出來。由表數據可知，D單位利潤最大，可以裝2件8噸，剩餘2噸選擇可以選擇利潤第二大的A，裝2件，此時最大利潤538元。