浮點數運算的誤差

在 JavaScript 中整數和浮點數都屬於number 數據類型，所有數字都是使用64位浮點數形式儲存，遵循IEEE-754雙精度標準存儲，即便整數也是如此。 所以我們在列印 1.00 這樣的浮點數的結果是 1 而非 1.00。而有時候用浮點數進行數學運算的時候，發現居然會有一些誤差，比如：

<script type="text/javascript">
    console.log("加法：");
    console.log("0.1 + 0.2 = " + (0.1 + 0.2));
    console.log("0.7 + 0.1 = " + (0.7 + 0.1));
    console.log("0.2 + 0.4 = " + (0.2 + 0.4));
    
    console.log("減法：");
    console.log("0.3 - 0.2 = " + (0.3 - 0.2));
    
    console.log("乘法：");
    console.log("19.9 * 100 = " + (19.9 * 100));
    console.log("9.7 * 100 = " + (9.7 * 100));
    
    console.log("除法：");
    console.log("0.3 / 0.1 = " + (0.3 / 0.1));
    console.log("0.69 / 10 = " + (0.69 / 10));
</script>

結果為：

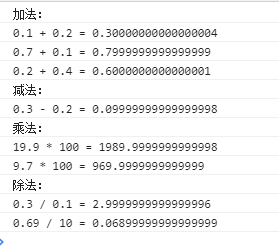
那麼原因在哪呢？？

JavaScript 里的數字是採用 IEEE 754 標準  的 64 位雙精度浮點數。該規範定義了浮點數的格式，對於64位的浮點數在記憶體中的表示，最高的1位是符號位，接著的11位是指數，剩下的52位為有效數字，具體：

其中：

• 符號位 s（Sign）決定數是正數（s＝0）還是負數（s＝1），而對於數值 0 的符號位解釋則作為特殊情況處理。
• 有效數字位 M（Significand）是二進位小數，它的取值範圍為 1~2^-ε，或者為 0~1^-ε。它也被稱為尾數位（Mantissa）、繫數位（Coefficient），甚至還被稱作“小數”
• 指數位 E（Exponent）是 2 的冪（可能是負數），它的作用是對浮點數加權。

符號位決定了一個數的正負，指數部分決定了數值的大小，小數部分決定了數值的精度。 IEEE 754規定，有效數字第一位預設總是1，不保存在64位浮點數之中。也就是說，有效數字總是1.xx…xx的形式，其中xx..xx的部分保存在64位浮點數之中，最長可能為52位。因此，JavaScript提供的有效數字最長為53個二進位位（64位浮點的後52位+有效數字第一位的1）。

那麼舉個例子：

計算 0.1 + 0.2 時，記憶體中發生的事：

首先，十進位的 0.1 和 0.2 都會被轉換成二進位，但由於浮點數用二進位表達時是無窮的，即

• 0.1 -> 0.0001100110011001...(無限)
• 0.2 -> 0.0011001100110011...(無限)

IEEE 754 標準的 64 位雙精度浮點數的小數部分最多支持 53 位二進位位，所以兩者相加之後得到二進位為：

• 0.0100110011001100110011001100110011001100110011001100

因浮點數小數位的限制而截斷的二進位數字，再轉換為十進位，就成了 0.30000000000000004。所以在進行算術計算時會產生誤差。

那麼怎麼解決這個誤差呢？

一般使用 toFixed() 方法 ，語法為：

數值.toFixed(num)；

num 是精確的位數，例如：

var num = 13.14520;
console.log(num.toFixed(2));

結果為： 13.14