我的LeetCode:https://leetcode cn.com/u/ituring/ 我的LeetCode刷題源碼[GitHub]:https://github.com/izhoujie/Algorithmcii LeetCode 11. 盛最多水的容器 題目 給你 n 個非負整數 a1,a2 ...
我的LeetCode:https://leetcode-cn.com/u/ituring/
我的LeetCode刷題源碼[GitHub]:https://github.com/izhoujie/Algorithmcii
LeetCode 11. 盛最多水的容器
題目
給你 n 個非負整數 a1,a2,...,an,每個數代表坐標中的一個點 (i, ai) 。在坐標內畫 n 條垂直線,垂直線 i 的兩個端點分別為 (i, ai) 和 (i, 0)。找出其中的兩條線,使得它們與 x 軸共同構成的容器可以容納最多的水。
說明:你不能傾斜容器,且 n 的值至少為 2。
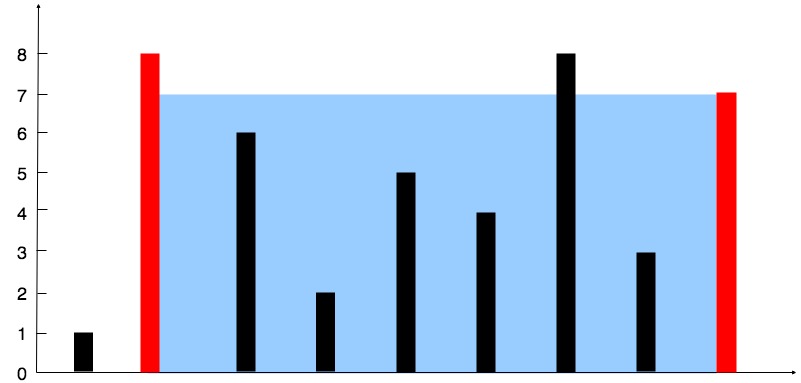
圖中垂直線代表輸入數組 [1,8,6,2,5,4,8,3,7]。在此情況下,容器能夠容納水(表示為藍色部分)的最大值為 49。
示例:
輸入:[1,8,6,2,5,4,8,3,7]
輸出:49
來源:力扣(LeetCode)
鏈接:https://leetcode-cn.com/problems/container-with-most-water
著作權歸領扣網路所有。商業轉載請聯繫官方授權,非商業轉載請註明出處。
解題思路
本題相像的是LeetCode 42. 接雨水,可以對比學習;
思路1-貪心演算法之雙指針遍歷
首先明確兩個擋板中的最小擋板決定了儲水上限,所以貪心或者說動態規劃時圍繞這個關鍵點展開;
步驟:
- 當前兩擋板中的最小值乘以擋板間距就是儲水量,每次都移動左右擋板一次,每次移動只有找到比當前最小擋板大的擋板時才停止(若小於,擋板高度不變但間距變小,出水量只會減少);
- 以當前兩個新擋板的最小值乘以其間距為最大儲水量,並對比1更新最大儲水量,然後迴圈進行1之後的操作直至左右擋板相遇;
演算法複雜度:
- 時間複雜度: $ {\color{Magenta}{\Omicron\left(N\right)}} $
- 空間複雜度: $ {\color{Magenta}{\Omicron\left(1\right)}} $
演算法源碼示例
package leetcode;
/**
* @author ZhouJie
* @date 2019年12月12日 下午9:34:10
* @Description: 11. 盛最多水的容器
*
*/
public class LeetCode_0011 {
}
class Solution_0011 {
public int maxArea(int[] height) {
int len = 0;
if (height == null || (len = height.length) < 2) {
return 0;
}
int i = 0, j = len - 1;
int max = 0;
int min = 0;
while (i < j) {
// 當前左右擋板中的小值
min = Math.min(height[i], height[j]);
// 記錄最大儲水
max = Math.max(max, min * (j - i));
// 向後找到第一個比min大的位置
while (i < j && height[i] <= min) {
i++;
}
// 向前找到第一個比min大的位置
while (i < j && height[j] <= min) {
j--;
}
}
return max;
}
}



