二值圖像連通域標記演算法優化

来源:https://www.cnblogs.com/kensporger/archive/2020/03/11/12463122.html
-Advertisement-
Play Games

文章概要 非常感謝☆Ronny丶博主在其博文《圖像分析：二值圖像連通域標記》中對二值圖像連通域的介紹和演算法闡述，讓我這個毫無數據結構演算法底子的小白能夠理解和復現代碼。本文的目的是基於我自己的理解，對該博文中Two-Pass演算法的一些優化和補充，同時也希望幫助更多像我一樣的人較快地掌握連通域標記。 連 ...


文章概要

 

　　非常感謝☆Ronny丶博主在其博文《圖像分析：二值圖像連通域標記》中對二值圖像連通域的介紹和演算法闡述，讓我這個毫無數據結構演算法底子的小白能夠理解和復現代碼。本文的目的是基於我自己的理解，對該博文中Two-Pass演算法的一些優化和補充，同時也希望幫助更多像我一樣的人較快地掌握連通域標記。

　　連通域標記是圖像分割計數的一個重要環節，在工業上應用非常地多。例如像硬幣的計件，在二值化處理後，為了能夠感知數量，就得對硬幣區域進行標記（當然標記前可能還要經過一系列的形態學處理）。另外，還有一個我想到的，更有趣、也更具有挑戰性的例子——二維碼連通域標記，這用來檢驗演算法的性能是再合適不過了。言歸正題——本文介紹了兩大流行演算法，一個是利用DFS的Seed-Filling演算法，另一個是Two-Pass演算法。後者因為處理等價對的方法不同，又細分為DFS Two-Pass（使用DFS處理等價對）和Union-Find Two-Pass（使用並查集處理等價對）。如果硬要給這三種演算法排序的話，大概是Union-Find Two-Pass > Seed-Filling > DFS Two-Pass，反正我寫的程式是這樣的速度排序。

 

Seed-Filling演算法

 

　　這個演算法其實實質就是DFS，筆者曾經有幸做過一個“水窪連通”的演算法題，當時就是用DFS或者BFS來做的，顯然，“水窪連通”也是屬於連通域標記問題的。DFS在這個問題上的思路是：優先地尋找一個完整連通域，在找的同時把他們都標記一下，找完一個完整連通域， 再去找下一個連通域。按照這個想法，程式無非就是維護一個堆棧或者隊列罷了，寫起來相對簡潔易懂。要說缺點的話，就是頻繁的堆棧操作可能會拉低程式的性能。

　　簡要地說明一下這部分代碼含義，故事就定義成小明踩水坑吧，雖然小明對我表示自己很文靜，只喜歡做數學題。首先，定義了一個二維矩陣labels，大小跟二值圖一樣。一開始labels都是標簽0，這是一個無效標簽，可以理解為是充滿迷霧的未知區域或者是已確定的非水坑區域。小明每到達一個新的單位域（也就是一個新像素），首先要先看看這個域是不是未曾踩過的水坑（未曾踩過的水坑其標簽為0且灰度值為255），如果是的話，那麼小明就原地開心地踩水坑了，踩過以後還不忘給它畫上一個大於0的標記（以標簽1為例）。接下來，小明回顧四周，又發現了接壤的另一個水坑， 於是又在該水坑上留下了標記1······這樣看似單調的迴圈，在小明眼裡卻是一次次奇妙的冒險。愉快的時光很短暫，小明不一會兒就發現身邊已經沒有“新鮮”的水坑了，傷心的同時回到最初的那個水坑，繼續朝遠方走去。漸漸地，眼前依稀出現了陌生又熟悉的水坑，重現微笑的小明決定要開啟新的旅途，因此標記1.0進化至2.0。

　　故事的結束，要額外補充一點，程式里要不停地將新的單位域加入隊列， 因此隊列遍歷其上限是動態的。

 1 vector<vector<int>> seedFilling(Mat src)
 2 {
 3     
 4     // 標簽容器，初始化為標記0
 5     vector<vector<int>> labels(src.rows, vector<int>(src.cols, 0));
 6     // 當前的種子標簽
 7     int curLabel = 1;
 8     // 四連通位置偏移
 9     pair<int, int> offset[4] = {make_pair(0, 1), make_pair(1, 0), make_pair(-1, 0), make_pair(0, -1)};
10     // 當前連通域中的單位域隊列
11     vector<pair<int, int>> tempList;
12 
13     for (int i = 0; i < src.rows; i++)
14     {
15         for (int j = 0; j < src.cols; j++)
16         {
17             // 當前單位域已被標記或者屬於背景區域, 則跳過
18             if (labels[i][j] != 0 || src.at<uchar>(i, j) == 0)
19             {
20                 continue;
21             }
22             // 當前單位域未標記並且屬於前景區域, 用種子為其標記
23             labels[i][j] = curLabel;
24             // 加入單位域隊列
25             tempList.push_back(make_pair(i, j));
26 
27             // 遍歷單位域隊列
28             for (int k = 0; k < tempList.size(); k++)
29             {
30                 // 四連通範圍內檢查未標記的前景單位域
31                 for (int m = 0; m < 4; m++)
32                 {
33                     int row = offset[m].first + tempList[k].first;
34                     int col = offset[m].second + tempList[k].second;
35                     // 防止坐標溢出圖像邊界
36                     row = (row < 0) ? 0: ((row >= src.rows) ? (src.rows - 1): row);
37                     col = (col < 0) ? 0: ((col >= src.cols) ? (src.cols - 1): col);
38                     
39                     // 鄰近單位域未標記並且屬於前景區域, 標記並加入隊列
40                     if (labels[row][col] == 0 && src.at<uchar>(row, col) == 255)
41                     {
42                         labels[row][col] = curLabel;
43                         tempList.push_back(make_pair(row, col));                       
44                     }
45                 }
46             }
47             // 一個完整連通域查找完畢，標簽更新
48             curLabel++;
49             // 清空隊列
50             tempList.clear();
51         }
52     }
53 
54     return labels;
55 }

 

Two-Pass演算法

 

等價對生成

 

　　關於Two-Pass的演算法原理可以參考上面提到的博文，原文還是很詳細的，唯一的遺憾就是後面程式的註釋有點少，看起來會吃力些，說白了就是自己菜。要找一張二維圖像中的連通域，很容易想到可以一行一行先把子區域找出來，然後再拼合成一個完整的連通域，因為從每一行找連通域是一件很簡單的事。這個過程中需要記錄每一個子區域，為了滿足定位要求，並且節省記憶體，我們需要記錄子區域所在的行號、區域開始的位置、結束的位置，當然還有一個表徵子區域總數的變數。需要註意的就是子區域開始位置和結束位置在行首和行末的情況要單獨拿出來考慮。

 1 // 查找每一行的子區域
 2 // numberOfArea：子區域總數 stArea：子區域開始位置  enArea：子區域結束位置  rowArea：子區域所在行號
 3 void searchArea(const Mat src, int &numberOfArea, vector<int> &stArea, vector<int> &enArea, vector<int> &rowArea)
 4 {
 5     for (int row = 0; row < src.rows; row++)
 6     {
 7         // 行指針
 8         const uchar *rowData = src.ptr<uchar>(row);
 9         
10         // 判斷行首是否是子區域的開始點
11         if (rowData[0] == 255)
12         {
13             numberOfArea++;
14             stArea.push_back(0);
15         }
16         
17         for (int col = 1; col < src.cols; col++)
18         {
19             // 子區域開始位置的判斷：前像素為背景，當前像素是前景
20             if (rowData[col - 1] == 0 && rowData[col] == 255)
21             {
22                 // 在開始位置更新區域總數、開始位置vector
23                 numberOfArea++;
24                 stArea.push_back(col);      
25             // 子區域結束位置的判斷：前像素是前景，當前像素是背景         
26             }else if (rowData[col - 1] == 255 && rowData[col] == 0)
27             {
28                 // 更新結束位置vector、行號vector
29                 enArea.push_back(col - 1);
30                 rowArea.push_back(row);
31             }
32         }
33         // 結束位置在行末
34         if (rowData[src.cols - 1] == 255)
35         {
36             enArea.push_back(src.cols - 1);
37             rowArea.push_back(row);
38         }
39     }
40 }

 

　　另外一個比較棘手的問題，如何給這些子區域標號，使得同一個連通域有相同的標簽值。我們給單獨每一行的子區域標號區分是很容易的事， 關鍵是處理相鄰行間的子區域關係（怎麼判別兩個子區域是連通的）。

 

 

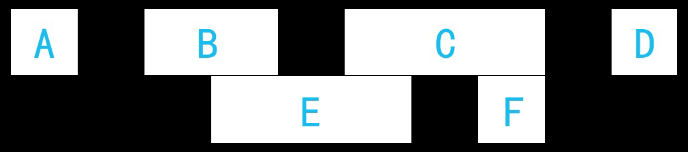
　　主要思路：以四連通為例，在上圖我們可以看出BE是屬於同一個連通域，判斷的依據是E的開始位置小於B的結束位置，並且E的結束地址大於B的開始地址；同理可以判斷出EC屬於同一個連通域，CF屬於同一個連通域，因此可以推知BECF都屬於同一個連通域。

　　迭代策略：尋找E的相連區域時，對前一行的ABCD進行迭代，找到相連的有B和C，而D的開始地址已經大於了E的結束地址，此時就可以提前break掉，避免不必要的迭代操作；接下來迭代F的時候，由於有E留下來的基礎，因此對上一行的迭代可以直接從C開始。另外，當前行之前的一行如果不存在子區域的話，那麼當前行的所有子區域都可以直接賦新的標簽，而不需要迭代上一行。

　　標簽策略：以上圖為例，遍歷第一行，A、B、C、D會分別得到標簽1、2、3、4。到了第二行，檢測到E與B相連，之前E的標簽還是初始值0，因此給E賦上B的標簽2；之後再次檢測到C和E相連，由於E已經有了標簽2，而C的標簽為3，則保持E和C標簽不變，將（2,3）作為等價對進行保存。同理，檢測到F和C相連，且F標簽還是初始值0，則為F標上3。如此對所有的子區域進行標號，最終可以得到一個等價對的列表。

　　下麵的代碼實現了上述的過程。子區域用一維vector保存，沒辦法直接定位到某一行號的子區域，因此需要用curRow來記錄當前的行，用firstAreaPrev記錄前一行的第一個子區域在vector中的位置，用lastAreaPrev記錄前一行的最後一個子區域在vector中的位置。在換行的時候，就去更新剛剛說的3個變數，其中firstAreaPrev的更新依賴於當前行的第一個子區域位置，所以還得用firstAreaCur記錄當前行的第一個子區域。

 1 // 初步標簽,獲取等價對
 2 // labelOfArea:子區域標簽值， equalLabels：等價標簽對 offset:0為四連通,1為8連通
 3 void markArea(int numberOfArea, vector<int> stArea, vector<int> enArea, vector<int> rowArea, vector<int> &labelOfArea, vector<pair<int, int>> &equalLabels, int offset)
 4 {
 5     int label = 1;
 6     // 當前所在行
 7     int curRow = 0;
 8     // 當前行的第一個子區域位置索引
 9     int firstAreaCur = 0;
10     // 前一行的第一個子區域位置索引
11     int firstAreaPrev = 0;
12     // 前一行的最後一個子區域位置索引
13     int lastAreaPrev = 0;
14 
15     // 初始化標簽都為0
16     labelOfArea.assign(numberOfArea, 0);
17     
18     // 遍歷所有子區域並標記
19     for (int i = 0; i < numberOfArea; i++)
20     {
21         // 行切換時更新狀態變數
22         if (curRow != rowArea[i])
23         {
24             curRow = rowArea[i];
25             firstAreaPrev = firstAreaCur;
26             lastAreaPrev = i - 1;
27             firstAreaCur = i;
28         }
29 
30         // 相鄰行不存在子區域
31         if (curRow != rowArea[firstAreaPrev] + 1)
32         {
33             labelOfArea[i] = label++;
34             continue;
35         }
36         // 對前一行進行迭代
37         for (int j = firstAreaPrev; j <= lastAreaPrev; j++)
38         {
39             // 判斷是否相連
40             if (stArea[i] <= enArea[j] + offset && enArea[i] >= stArea[j] - offset)
41             {
42                 if (labelOfArea[i] == 0)
43                     // 之前沒有標記過
44                     labelOfArea[i] = labelOfArea[j];
45                 else if (labelOfArea[i] != labelOfArea[j])
46                     // 之前已經被標記，保存等價對
47                     equalLabels.push_back(make_pair(labelOfArea[i], labelOfArea[j]));
48             }else if (enArea[i] < stArea[j] - offset)
49             {
50                 // 為當前行下一個子區域縮小上一行的迭代範圍
51                 firstAreaPrev = max(firstAreaPrev, j - 1);
52                 break;
53             }
54         }
55         // 與上一行不存在相連
56         if (labelOfArea[i] == 0)
57         {
58             labelOfArea[i] = label++;
59         }
60     }
61 }

 

 

DFS Two-Pass演算法

 

　　通過上面的努力，標記任務並沒有做完，最核心的部分正是如何處理等價對。這裡簡單貼上原博主說的DSF方法，又是深搜啊。相比於直接DFS標記連通域，先找等價對再深搜減少了大量的堆棧操作，因為前者深度取決於連通域的大小，而後者是連通域數量，顯然這兩個數量級的差距挺大的。

　　原博主的想法是建立一個Bool型等價對矩陣，用作深搜環境。具體做法是先獲取最大的標簽值maxLabel，然後生成一個$maxLabel*maxLabel$大小的二維矩陣，初始值為false；對於例如（1，3）這樣的等價對，在矩陣的（0，2）和（2，0）處賦值true——要註意索引和標簽值是相差1的。就這樣把所有等價對都反映到矩陣上。

　　深搜的目的在於建立一個標簽的重映射。例如4、5、8是等價的標簽，都重映射到標簽2。最後重映射的效果就是標簽最小為1，且依次遞增，沒有缺失和等價。深搜在這裡就是優先地尋找一列等價的標簽，例如一口氣把4、5、8都找出來，然後給他們映射到標簽2。程式也維護了一個隊列，當標簽在矩陣上值為true，而且沒有被映射過，就加入到隊列。

　　當然不一定要建立一個二維等價矩陣，一般情況，等價對數量要比maxLabel來的小，所以也可以直接對等價對列表進行深搜，但無論採用怎樣的深搜，其等價對處理的性能都不可能提高很多。

 1 // 等價對處理，標簽重映射
 2 void replaceEqualMark(vector<int> &labelOfArea, vector<pair<int, int>> equalLabels)
 3 {
 4     int maxLabel = *max_element(labelOfArea.begin(), labelOfArea.end());
 5     // 等價標簽矩陣，值為true表示這兩個標簽等價
 6     vector<vector<bool>> eqTab(maxLabel, vector<bool>(maxLabel, false));
 7     // 將等價對信息轉移到矩陣上
 8     vector<pair<int, int>>::iterator labPair;
 9     for (labPair = equalLabels.begin(); labPair != equalLabels.end(); labPair++)
10     {
11         eqTab[labPair->first -1][labPair->second -1] = true;
12         eqTab[labPair->second -1][labPair->first -1] = true;
13     }
14     // 標簽映射
15     vector<int> labelMap(maxLabel + 1, 0);
16     // 等價標簽隊列
17     vector<int> tempList;
18     // 當前使用的標簽
19     int curLabel = 1;
20 
21     for (int i = 1; i <= maxLabel; i++)
22     {
23         // 如果該標簽已被映射，直接跳過
24         if (labelMap[i] != 0)
25         {
26             continue;
27         }
28 
29 
30         labelMap[i] = curLabel;
31         tempList.push_back(i);
32 
33         for (int j = 0; j < tempList.size(); j++)
34         {
35             // 在所有標簽中尋找與當前標簽等價的標簽
36             for (int k = 1; k <= maxLabel; k++)
37             {
38                 // 等價且未訪問
39                 if (eqTab[tempList[j] - 1][k - 1] && labelMap[k] == 0)
40                 {
41                     labelMap[k] = curLabel;
42                     tempList.push_back(k);
43                 }
44             }
45         }
46 
47         curLabel++;
48         tempList.clear();
49     }
50     // 根據映射修改標簽
51     vector<int>::iterator label;
52     for (label = labelOfArea.begin(); label != labelOfArea.end(); label++)
53     {
54         *label = labelMap[*label];
55     }
56 
57 }

 

 

Union-Find Two-Pass演算法

 

　　如果讀者看到了這裡，真的要感謝一下您的耐心。Two-Pass演算法的代碼要比直接深搜來得多，用不好甚至性能還遠不如深搜。原博主在文中提及了可以用稀疏矩陣來處理等價對，奈何我較為愚鈍，讀者可以自研之。

　　講到等價對，實質是一種關係分類，因而聯想到並查集。並查集方法在這個問題上顯得非常合適，首先將等價對進行綜合就是合併操作，標簽重映射就是查詢操作（並查集可以看做一種多對一映射）。並查集具體演算法我就不嘮叨了，畢竟不怎麼打程式設計競賽。不過，採用並查集的話，函數定義估計就滿天飛了，這裡我包裝了一下，做成了類——實在是有點強迫症，其中等價對生成的函數方法跟上面的是一樣的。

　　網上有一些代碼也實現了這個演算法，但是有的犧牲了秩優化，合併時讓樹指向較小的根，個人認為這樣做太不值了。所以為瞭解決這個，我在並查集映射後，又用labelReMap來進行第二次的映射，主要的步驟跟前面的差不多。

　　然後，自己跑了一下這代碼，不算畫圖標記的時間，效率要比上面的快四五倍左右，實時性上肯定是綽綽有餘了。

  1 class AreaMark
  2 {
  3     public:
  4         AreaMark(const Mat src,int offset);
  5         int getMarkedArea(vector<vector<int>> &area); 
  6         void getMarkedImage(Mat &dst);
  7 
  8     private:
  9         Mat src; 
 10         int offset;
 11         int numberOfArea=0;
 12         vector<int> labelMap;
 13         vector<int> labelRank;
 14         vector<int> stArea; 
 15         vector<int> enArea;
 16         vector<int> rowArea;
 17         vector<int> labelOfArea;
 18         vector<pair<int, int>> equalLabels;
 19         
 20         void markArea();
 21         void searchArea();
 22         void setInit(int n);
 23         int findRoot(int label);
 24         void unite(int labelA, int labelB);
 25         void replaceEqualMark();
 26 };
 27 
 28 // 構造函數
 29 // imageInput:輸入待標記二值圖像    offsetInput:0為四連通，1為八連通
 30 AreaMark::AreaMark(Mat imageInput,int offsetInput)
 31 {
 32     src = imageInput;
 33     offset = offsetInput;
 34 }
 35 
 36 // 獲取顏色標記圖片
 37 void AreaMark::getMarkedImage(Mat &dst)
 38 {
 39     Mat img(src.rows, src.cols, CV_8UC3, CV_RGB(0, 0, 0));
 40     cvtColor(img, dst, CV_RGB2HSV);
 41     
 42     int maxLabel = *max_element(labelOfArea.begin(), labelOfArea.end());
 43     vector<uchar> hue;
 44     for (int i = 1; i<= maxLabel; i++)
 45     {
 46         // 使用HSV模型生成可區分顏色
 47         hue.push_back(uchar(180.0 * (i - 1) / (maxLabel + 1)));
 48     }
 49 
 50     for (int i = 0; i < numberOfArea; i++)
 51     {
 52         for (int j = stArea[i]; j <= enArea[i]; j++)
 53         {
 54             dst.at<Vec3b>(rowArea[i], j)[0] = hue[labelOfArea[i]];
 55             dst.at<Vec3b>(rowArea[i], j)[1] = 255;
 56             dst.at<Vec3b>(rowArea[i], j)[2] = 255;
 57         }
 58     }
 59 
 60     cvtColor(dst, dst, CV_HSV2BGR);
 61 } 
 62 
 63 // 獲取標記過的各行子區域
 64 int AreaMark::getMarkedArea(vector<vector<int>> &area)
 65 {
 66     searchArea();
 67     markArea();
 68     replaceEqualMark();
 69     area.push_back(rowArea);
 70     area.push_back(stArea);
 71     area.push_back(enArea);
 72     area.push_back(labelOfArea);
 73     return numberOfArea;
 74 }
 75 
 76 void AreaMark::searchArea()
 77 {
 78     for (int row = 0; row < src.rows; row++)
 79     {
 80         // 行指針
 81         const uchar *rowData = src.ptr<uchar>(row);
 82         
 83         // 判斷行首是否是子區域的開始點
 84         if (rowData[0] == 255)
 85         {
 86             numberOfArea++;
 87             stArea.push_back(0);
 88         }
 89         
 90         for (int col = 1; col < src.cols; col++)
 91         {
 92             // 子區域開始位置的判斷：前像素為背景，當前像素是前景
 93             if (rowData[col - 1] == 0 && rowData[col] == 255)
 94             {
 95                 // 在開始位置更新區域總數、開始位置vector
 96                 numberOfArea++;
 97                 stArea.push_back(col);      
 98             // 子區域結束位置的判斷：前像素是前景，當前像素是背景         
 99             }else if (rowData[col - 1] == 255 && rowData[col] == 0)
100             {
101                 // 更新結束位置vector、行號vector
102                 enArea.push_back(col - 1);
103                 rowArea.push_back(row);
104             }
105         }
106         // 結束位置在行末
107         if (rowData[src.cols - 1] == 255)
108         {
109             enArea.push_back(src.cols - 1);
110             rowArea.push_back(row);
111         }
112     }
113 }
114 
115 
116 
117 void AreaMark::markArea()
118 {
119     int label = 1;
120     // 當前所在行
121     int curRow = 0;
122     // 當前行的第一個子區域位置索引
123     int firstAreaCur = 0;
124     // 前一行的第一個子區域位置索引
125     int firstAreaPrev = 0;
126     // 前一行的最後一個子區域位置索引
127     int lastAreaPrev = 0;
128 
129     // 初始化標簽都為0
130     labelOfArea.assign(numberOfArea, 0);
131     
132     // 遍歷所有子區域並標記
133     for (int i = 0; i < numberOfArea; i++)
134     {
135         // 行切換時更新狀態變數
136         if (curRow != rowArea[i])
137         {
138             curRow = rowArea[i];
139             firstAreaPrev = firstAreaCur;
140             lastAreaPrev = i - 1;
141             firstAreaCur = i;
142         }
143 
144         // 相鄰行不存在子區域
145         if (curRow != rowArea[firstAreaPrev] + 1)
146         {
147             labelOfArea[i] = label++;
148             continue;
149         }
150         // 對前一行進行迭代
151         for (int j = firstAreaPrev; j <= lastAreaPrev; j++)
152         {
153             // 判斷是否相連
154             if (stArea[i] <= enArea[j] + offset && enArea[i] >= stArea[j] - offset)
155             {
156                 if (labelOfArea[i] == 0)
157                     // 之前沒有標記過
158                     labelOfArea[i] = labelOfArea[j];
159                 else if (labelOfArea[i] != labelOfArea[j])
160                     // 之前已經被標記，保存等價對
161                     equalLabels.push_back(make_pair(labelOfArea[i], labelOfArea[j]));
162             }else if (enArea[i] < stArea[j] - offset)
163             {
164                 // 為當前行下一個子區域縮小上一行的迭代範圍
165                 firstAreaPrev = max(firstAreaPrev, j - 1);
166                 break;
167             }
168         }
169         // 與上一行不存在相連
170         if (labelOfArea[i] == 0)
171         {
172             labelOfArea[i] = label++;
173         }
174     }
175 }
176
您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • MyBatis源碼解析 - 反射模塊
    MyBatis源碼解析 反射模塊 1. 前言 ​ 該模塊位於 包中，MyBatis在進行參數處理、結果映射等操作時，會涉及大量的反射操作。Java 中的反射雖然功能強大，但是代碼編寫起來比較複雜且容易出錯，為了簡化反射操作的相關代碼，MyBatis提供了專門的反射模塊，它對常見的反射操作做了進一步封 ...
  • java 構造函數調用構造函數、this()語句
    this語句：用於構造函數之間進行相互調用 this(屬性) this()語句只能定義在構造函數的第一行。因為初始化動作要先執行。 ...
  • Java併發：join與wait
    Thread.join中使用Object.wait實現： //java.lang.Thread public final synchronized void join(long millis) throws InterruptedException { long base = System.curr ...
  • MyBatis源碼解析 - 解析器模塊
    MyBatis源碼解析 解析器模塊 1. 前言 在MyBatis中涉及多個xml文件，解析這些xml文件自然離不開解析器。本文就來分析一下解析器模塊。 2. 準備工作 xml常見的解析方式分為以下三種： DOM ( Document Object Model)解析方式 SAX (Simple API ...
  • MyBatis 源碼分析-項目總覽
    MyBatis 源碼分析 項目總覽 1.概述 本文主要大致介紹一下MyBatis的項目結構。 引用參考資料《MyBatis技術內幕》 此外，https://mybatis.org/mybatis 3/zh/index.html MyBatis官方也提供了很不錯的中文文檔。對於使用中有碰到一些問題，可 ...
  • MyBatis源碼解析-搭建調試環境
    MyBatis源碼解析 搭建調試環境 1. 相關工具 Maven Git JDK1.8 IntelliJ IDEA 2. 源碼拉取 一般來說，我們直接從https://github.com/mybatis/mybatis 3 Fork到自己的倉庫中，為什麼要Fork呢？我們在之後的源碼分析中，我們可 ...
  • Redis的持久化方案
    Redis支持RDB與AOF兩種持久化機制，持久化可以避免因進程異常退出或down機導致的數據丟失問題，在下次重啟時能利用之前的持久化文件實現數據恢復。 RDB持久化 RDB持久化即通過創建快照（壓縮的二進位文件）的方式進行持久化，保存某個時間點的全量數據。RDB持久化是Redis預設的持久化方式。 ...
  • shell編程入門
    最近由於工作原因，寫了幾個腳本，然後再linux中用定時任務去跑，記錄一下shell腳本的學習過程吧！ 首先知道shell第一行#!/bin/bash表示這是一個shell腳本，例如下麵這個簡單的腳本： #!/bin/bash #author:java小新人 #date:20200311 #desc ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類