P1034 矩形覆蓋

題目描述

在平面上有n個點（n<=50），每個點用一對整數坐標表示。例如：當n＝4時，4個點的坐標分另為：p1（1，1），p2（2，2），p3（3，6），P4（0，7），見圖一。

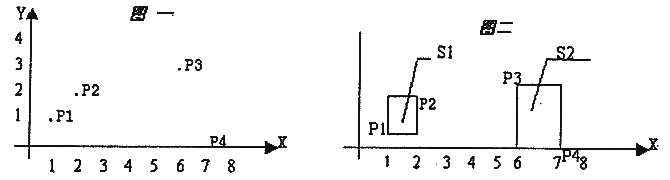
這些點可以用 k 個矩形（1<=k<=4）全部覆蓋，矩形的邊平行於坐標軸。當 k=2 時，可用如圖二的兩個矩形 sl，s2 覆蓋，s1，s2 面積和為 4。問題是當 n 個點坐標和 k 給出後，怎樣才能使得覆蓋所有點的 k 個矩形的面積之和為最小呢。約定：覆蓋一個點的矩形面積為 0；覆蓋平行於坐標軸直線上點的矩形面積也為0。各個矩形必須完全分開（邊線與頂點也都不能重合）。

輸入格式

n k
xl y1
x2 y2
… …
xn yn
(0<=xi,yi<=500)

輸出格式

輸出至屏幕。格式為：
一個整數，即滿足條件的最小的矩形面積之和。

輸入輸出樣例

輸入

4 2
1 1
2 2
3 6
0 7

輸出

4

分析

主要是搜索。
這題剪枝方法似乎多種多樣。
下麵將要展示代碼的做法：
將讀入的坐標按x和y從小到大排序，然後搜索將連續的i個點分在一起，期間判斷問題是否可行，以及進行各種小優化。
Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct point{
    int x,y;
}a[60];
int cmp(point a,point b){
    if(a.x==b.x)return a.y<b.y;
    return a.x<b.x;
}
struct block{
    int x1,y1,x2,y2;
}b[5];
int n,k;
int ans=1e9;
void DFS(int pos,int cnt,int smm){
    if(pos>n){
        ans=min(ans,smm);
        return;
    }
    if(cnt>k)return;
    int i,j;
    b[cnt].x1=a[pos].x;
    b[cnt].x2=a[pos].x;
    b[cnt].y1=a[pos].y;
    b[cnt].y2=a[pos].y;
    for(i=pos;i<=n;i++){
        b[cnt].y2=max(b[cnt].y2,a[i].y);
        b[cnt].x2=max(b[cnt].x2,a[i].x);
        b[cnt].x1=min(b[cnt].x1,a[i].x);
        b[cnt].y1=min(b[cnt].y1,a[i].y);
        for(j=1;j<cnt;j++){
            if(b[cnt].x1<=b[j].x2 && b[cnt].y1<=b[j].y2)return;
        }
        if(i<n && cnt==k)continue;
        DFS(i+1,cnt+1,smm+(b[cnt].x2-b[cnt].x1)*(b[cnt].y2-b[cnt].y1));
    }
    return;
}
int main(){
    n=read();k=read();
    int i,j;
    for(i=1;i<=n;i++){
        a[i].y=read();a[i].x=read();
    }
    sort(a+1,a+n+1,cmp);
    memset(b,-1,sizeof b);
    DFS(1,1,0);
    printf("%d\n",ans);
    return 0;
}