圖的基本概念 首先,你要明確圖是什麼樣子的,就是下麵這個樣子的 圖的定義與術語 有向圖和無向圖 直接對比圖就可以看出來,有向圖和無向圖的區別了,這個沒有什麼難的。 有向圖和無向圖的表示法有略微的區別,註意看 G1有箭頭,有向圖,表示方法是 G2無箭頭,無向圖,表示方法是 弧、弧頭、弧尾:有向圖的邊稱 ...
圖的基本概念
首先,你要明確圖是什麼樣子的,就是下麵這個樣子的
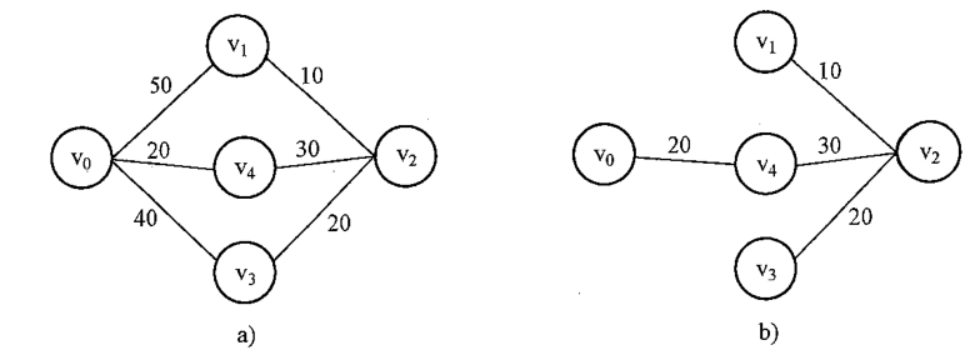
圖的定義與術語
有向圖和無向圖
直接對比圖就可以看出來,有向圖和無向圖的區別了,這個沒有什麼難的。
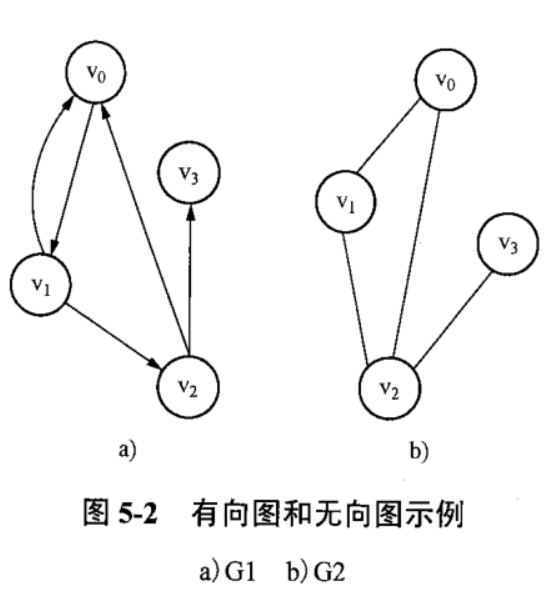
有向圖和無向圖的表示法有略微的區別,註意看
G1有箭頭,有向圖,表示方法是 V={V~0~,V~1~,V~2~,V~3~} E = {<V~0~,V~1~>,<V~1~,V~2~>,<V~1~,V~0~>,<V~2~,V~0~>,<V~2~,V~3~>}
G2無箭頭,無向圖,表示方法是 V={V~0~,V~1~,V~2~,V~3~} E = {(V~0~,V~1~),(V~1~,V~2~),(V~0~,V~2~),(V~2~,V~3~)}
弧、弧頭、弧尾:有向圖的邊稱為弧。無向圖叫做邊。有序偶對<v,w>表示有向圖從v到w的一條弧,v稱為弧尾或始點,w稱為弧頭或終點。
任何兩點之間都有邊的無向圖稱為無向完全圖。
任何兩點之間都有弧的有向圖稱為有向完全圖。
權、帶權圖:圖的邊附帶數值,這個數值叫權。每條邊都帶權的圖稱為帶權圖。
頂點的度、入度、出度:
- 無向圖中頂點v的度是與該頂點相關聯的邊的數目,記為D(v)。
- 有向圖中,把以頂點v為終點的弧的數目稱為v的入度,記為ID(v);把以頂點v為始點的弧的數目稱為v的出度,記為OD(v)。有向圖頂點v的度為入度和出度之和,即D(v) = ID(v)+ OD(v)。
簡單路徑、迴路、簡單迴路:序列中頂點不重覆出現的路徑稱為簡單路徑。第一個頂點和最後一個頂點相同的路徑稱為迴路。除了第一個頂點和最後一個頂點外,其餘頂點不重覆的迴路,稱為簡單迴路或簡單環。
下麵還有一些需要瞭解的術語
連通、連通圖、連通分量、極大連通子圖、強連通、強連通圖、強連通分量、生成樹、生成森林
如果精力足夠,都看看吧
圖的存儲結構
圖的存儲結構有很多中,例如 鄰接矩陣、鄰接表、十字鏈表和鄰接多重表
鄰接矩陣
矩陣中標記1,有邊,標記0,沒有邊
註意:無向圖的鄰接矩陣是一個對稱矩陣

帶權圖的鄰接矩陣
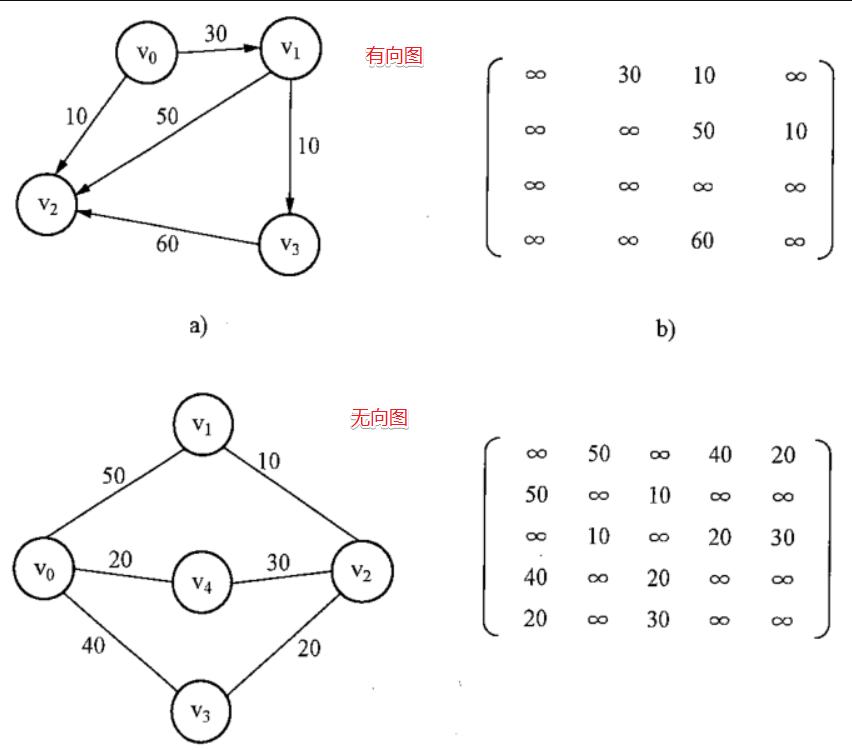
鄰接矩陣自考/期末考試真題

嘗試著,畫出無向圖吧!
鄰接表
鄰接表是順序存儲與鏈式存儲相結合的存儲方法。
下圖中,左側是無向圖,右側是該無向圖的鄰接表,註意看,∧該符號,表示結束,沒有連接的頂點了。
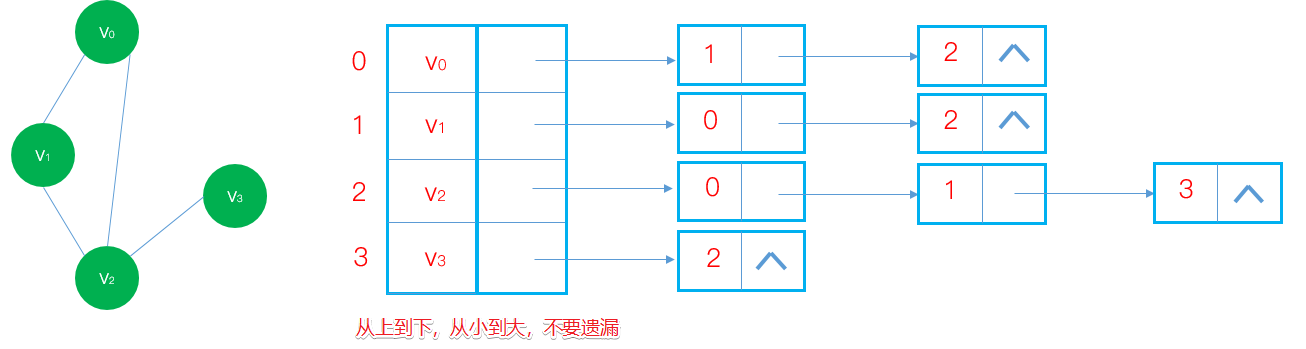
有向圖及其類似,這個就不在做圖擴充
圖的遍歷
圖的遍歷是指從圖的某個頂點出發,系統地訪問圖的每個頂點,並且每個頂點只被訪問一次。
遍歷圖的基本方法有兩種:深度優先搜索和廣度優先搜索。
連通圖的深度優先搜索
深度優先,就是往下走,走不動了,返回上一級在走
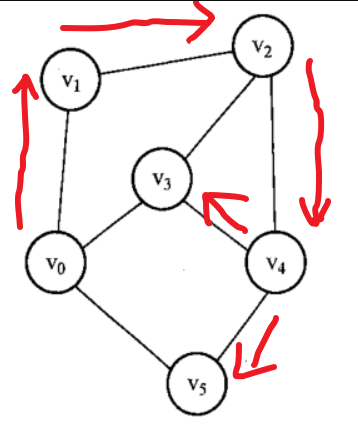
連通圖的廣度優先搜索
順著一個頂點,然後都遍歷完。
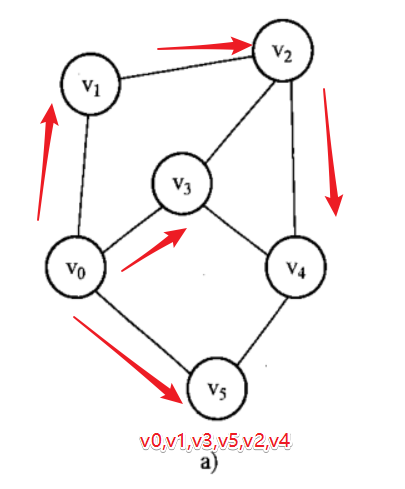
圖的應用
最小生成樹的概念
概念:一個圖的最小生成樹是圖所有生成樹中權總和最小的生成樹
構造最小生成樹的Prim演算法
每次都找權值最小的
看案例
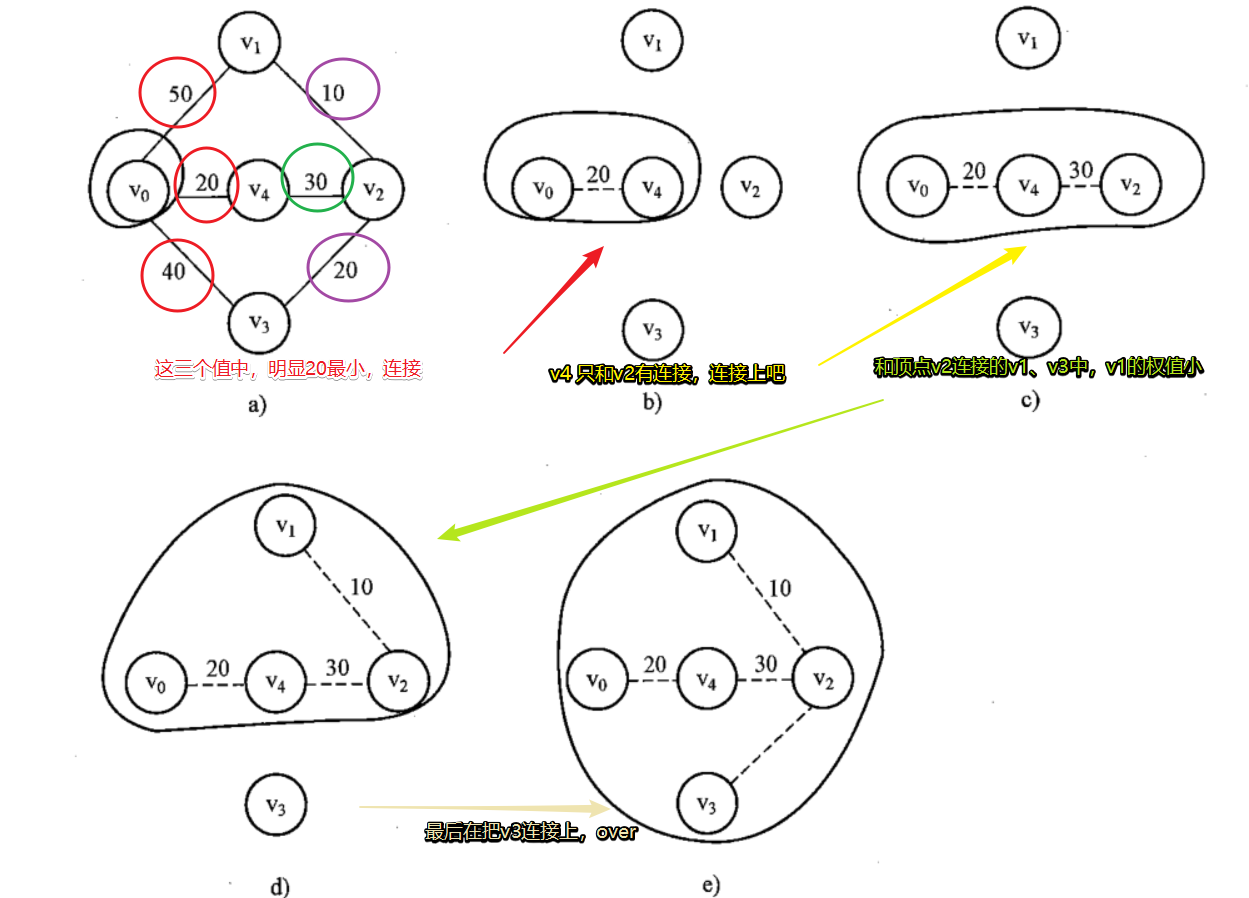
構造最小生成樹的克魯斯卡爾演算法 與 單源最短路徑 這兩種演算法,自己看一下吧。
拓撲排序
AOV網
工程或者某種流程可以分為若幹個小的工程或階段,這些小的工程或階段就稱為活動。
如果以圖中的頂點來表示活動,有向邊表示活動之間的優先關係,這種用頂點表示活動的有向圖稱為AOV網。
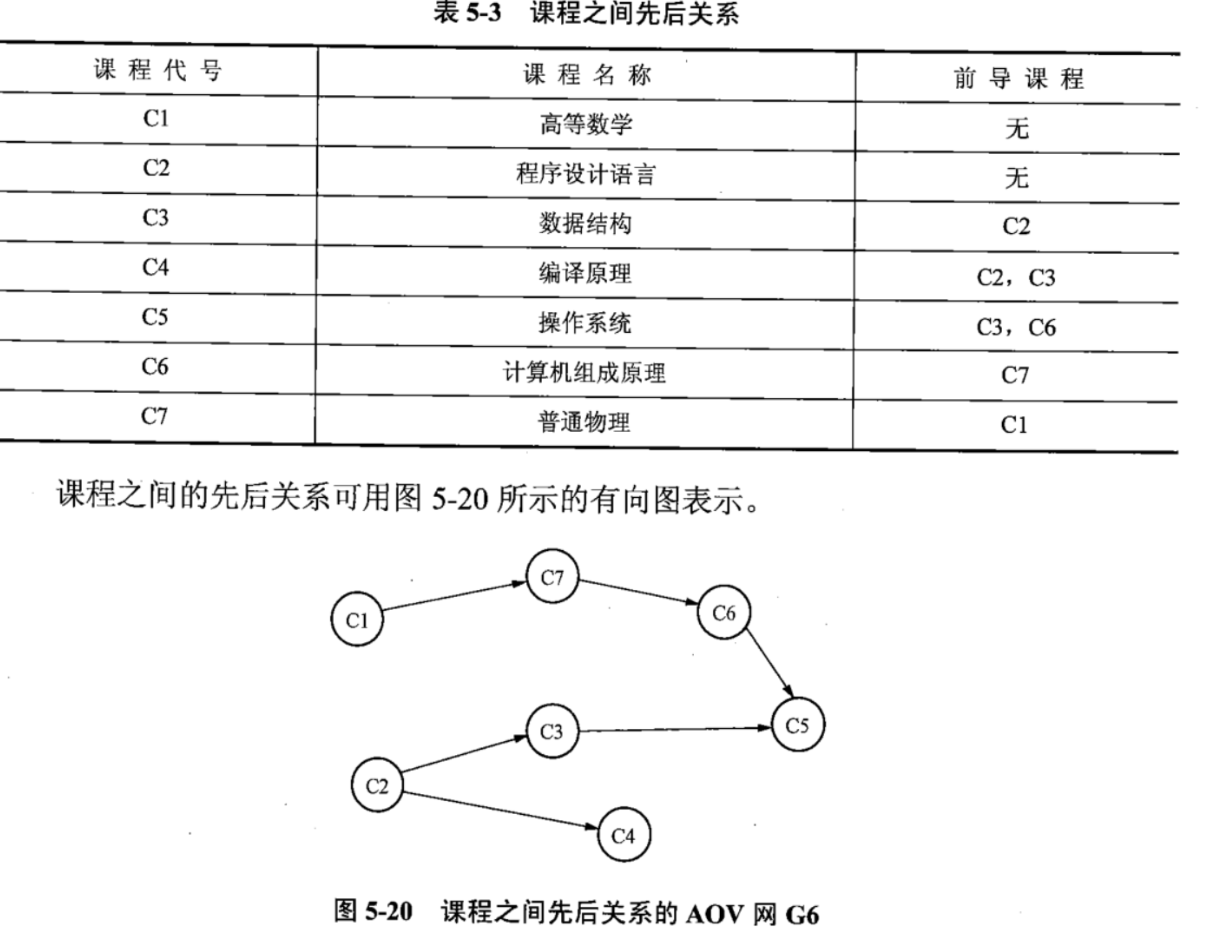
- 拓撲排序
設G=(V,E) 是一個具有n個頂點的有向圖,V中頂點的序列v~1~,v~2~,...,v~n~稱為一個拓撲序列,當且僅當該頂點序列滿足下列條件:若在有向圖G中,從頂點v~i~ ~ v~j~ 有一條路徑,則在拓撲序列中頂點v~i~必須排在v~j~之前。找到一個有向圖的一個拓撲序列的過程稱為拓撲排序。完成拓撲排序的前提條件是AOV網中不允許出現迴路。
拓撲排序演算法的時間複雜度為O(n+e),n是圖的頂點個數,e是圖的弧的數目。
拓撲排序演算法的基本步驟如下:
- 圖中選擇一個入度為0的頂點,輸出該頂點
- 從圖中刪除該頂點及相關聯的弧,調整被刪弧的弧頭結點的入度(入度減1);
- 重覆執行上述兩個步驟,直到所有的入度為0
好好理解一下拓撲排序演算法吧
自考/數據結構期末考試真題
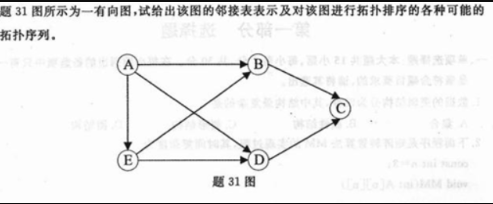
畫圖說明步驟
更多圖示: https://dwz.cn/r4lCXEuL
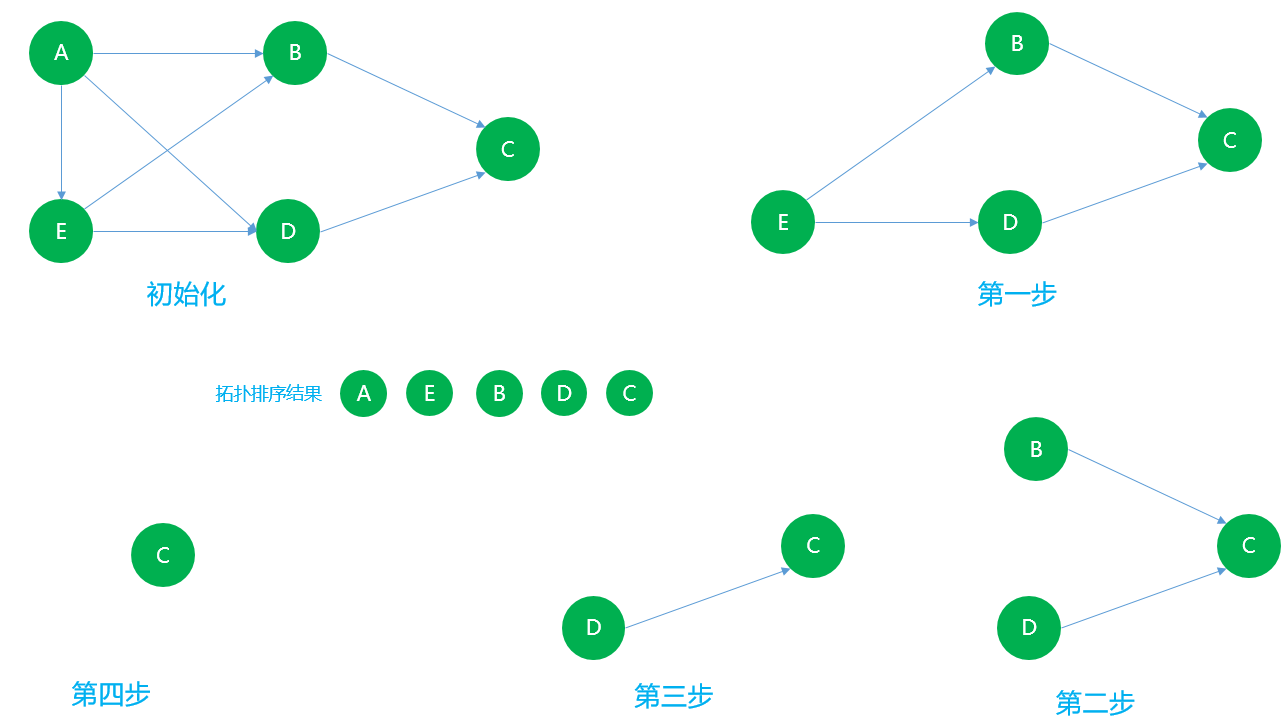
拓撲排序不唯一~



