Java的HashMap源碼中用到的(n-1)&hash這樣的運算,查找發現這是一種高效的求餘數的辦法,但其中的原理是什麼呢為什麼可以這麼做呢? 先上結論:假設被除數是x,對於除數是2n的取餘操作x%2n,都可以寫成x&(2n-1),位運算效率高! eg:259%8=259&7=3 259 1000 ...
Java的HashMap源碼中用到的(n-1)&hash這樣的運算,查找發現這是一種高效的求餘數的辦法,但其中的原理是什麼呢為什麼可以這麼做呢?
先上結論:假設被除數是x,對於除數是2n的取餘操作x%2n,都可以寫成x&(2n-1),位運算效率高!
eg:259%8=259&7=3 259 100000011 7 000000111 259&7=011=3
網上對這個原因的解釋都是模糊不清,下麵是我對於這個等式為什麼成立的一些理解。
就拿上面這個259%8進行舉例。
259的二進位為100000011,8的二進位為1000。
假如對8進行取餘,那麼只需要留下最後4位,前面的都可以捨棄,為什麼呢?
因為比8更高位的都來自於8的2次冪,所以高位的1都是可以整除8,可以直接捨棄。
這解釋了為什麼只有除數是2n才可以這樣的操作,因為如果除數是9的話,高位不一定能整除9,無法捨棄所以不行。(其餘2n除數也同理)
也解釋了為什麼位數不同也可以做&操作,因為比除數高的位都是可以捨棄的。
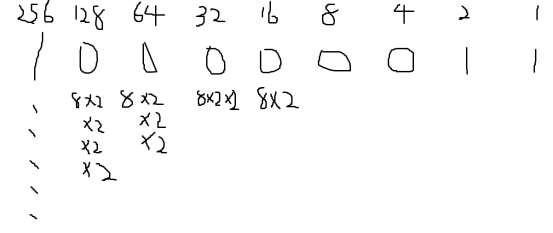
然後就是&操作了,直接&8的話是不行的,假設最後四位是1XXX,那麼1XXX&1000=1000,很明顯對8取餘得到的結果不可能是8,餘數應在0到除數減一之間,
所以我們需要對&7,讓取餘結果最大在0-7之間。
這就解釋了為什麼要&(2n-1)。
那有些人會問了,那我就是要&8,不就是相當於對9取餘嗎?
對9取餘就違反了上面的:“只有除數是2n才可以這樣的操作”
以上是個人對這個取餘原理的理解,歡迎討論



