前言: 關聯規則是數據挖掘中最活躍的研究方法之一, 是指搜索業務系統中的所有細節或事務,找出所有能把一 組事件或數據項與另一組事件或數據項聯繫起來的規則,以獲 得存在於資料庫中的不為人知的或不能確定的信息,它側重於確 定數據中不同領域之間的聯繫,也是在無指導學習系統中挖掘本地模式的最普通形式。 一般 ...
前言:
關聯規則是數據挖掘中最活躍的研究方法之一, 是指搜索業務系統中的所有細節或事務,找出所有能把一 組事件或數據項與另一組事件或數據項聯繫起來的規則,以獲 得存在於資料庫中的不為人知的或不能確定的信息,它側重於確 定數據中不同領域之間的聯繫,也是在無指導學習系統中挖掘本地模式的最普通形式。
一般來說,關聯規則挖掘是指從一個大型的數據集(Dataset)發現有趣的關 聯(Association)或相關關係(Correlation),即從數據集中識別出頻繁 出現的屬性值集(Sets of Attribute Values),也稱為頻繁項集 (Frequent Itemsets,頻繁集),然後利用這些頻繁項集創建描述關聯關係的規則的過程。
關聯規則挖掘問題:
發現頻繁項集:現所有的頻繁項集是形成關聯規則的基礎。通過用戶給定的最 小支持度,尋找所有支持度大於或等於Minsupport的頻繁項集。
生成關聯規則:通過用戶給定的最小可信度,在每個最大頻繁項集中,尋找可信度不小於Minconfidence的關聯規則.
如何迅速高效地發現所有頻繁項集,是關聯規則挖掘的核心問題,也是衡量關聯規則挖掘演算法效率的重要標準。
經典的挖掘完全頻繁項集方法是查找頻繁項集集合的全集。其中包括基於廣度優先演算法搜索的 關聯規則演算法--Apriori演算法(通過多次迭代找出所有的頻繁項集)及DHP(Direct Hashing Pruning) 演算法等改進演算法;基於深度優先搜索策略的FP-Growth演算法,ECLAT演算法,COFI演算法等, 我將介紹兩種經典演算法--Apriori演算法和FP-Growth演算法。
1.Apriori演算法
Apriori演算法基於頻繁項集性質的先驗知識,使用由下至上逐層搜索的迭代方法, 即從頻繁1項集開始,採用頻繁k項集搜索頻繁k+1項集,直到不能找到包含更多項的頻繁項集為止。
Apriori演算法由以下步驟組成,其中的核心步驟是連接步和剪枝步:

Apriori演算法由以下步驟組成,其中的核心步驟是連接步和剪枝步
(1)生成頻繁1項集L1。
(2)連接步:為了尋找頻繁k項集 ,首先生成一個潛在頻繁k項集構成的候選項集 , 中的每一個項集是由兩個只有一項不同的屬於 的頻繁項集做k-2連接運算得到的。連接方法為:設l1和l2是 中的項集,即 ,如果l1和l2中的前k-2個元素相同,則稱l1和l2是可連接的,用 表示。假定事務資料庫中的項均按照字典順序排列,li[j]表示li中的第j項,則連接l1和l2的結果項集是 。
(3)剪枝步:連接步生成的Ck是Lk的超集,包含所有的頻繁項集Lk,同時也可能包含一些非頻繁項集。可以利用前述先驗知識(定理3.2),進行剪枝以壓縮數據規模。比如,如果候選k項集Ck的k-1項子集不在Lk-1中,那麼該子集不可能是頻繁項集,可以直接刪除。
(4)生成頻繁k項集Lk:掃描事務資料庫D,計算Ck中每個項集的支持度,去除不滿足最小支持度的項集,得到頻繁k項集Lk。
(5)重覆步驟(2)~(4),直到不能產生新的頻繁項集的集合為止,演算法中止。
Apriori演算法是一種基於水平數據分佈的、寬度優先的演算法,由於 使用了層次搜索策略和剪枝技術,使得Apriori演算法在挖掘頻繁模式時具 有較高的效率。但是,Apriori演算法也有兩個致命的性能瓶頸:
(1)Apriori演算法是一個多趟搜索演算法,每次搜索都要掃描事務資料庫,I/O開銷巨大。對於候選k項集Ck來說,必須掃描其中的每個元素以確認是否加入頻繁k項集Lk,若候選k項集Ck中包含n項,則至少需要掃描事務資料庫n次。
(2)可能產生龐大的候選項集。由於針對頻繁項集Lk-1的k-2連接運算,由Lk-1 產生的候選k項集Ck是呈指數增長的,如此海量的候選集對於電腦的運算時間和 存儲空間都是巨大的挑戰。
| 交易 | 商品代碼 |
| T100 | L1,L2,L3 |
| T200 | L2,L3 |
| T300 | L2,L3 |
| T400 | L1,L2,L4 |
| T500 | L1,L3 |
| T600 | L2,L3 |
| T700 | L1,L3 |
| T800 | L1,L2,L3,L5 |
| T900 | L1,L2,L3 |
當K=1,min_sup=1時
計算C1和L1
| C1 | |
| 項集 | 支持度計數 |
| {L1} | 6 |
| {L2} | 7 |
| {L3} | 6 |
| {L4} | 2 |
| {L5} | 2 |
| L1:由C1剪枝得到L1 | |
| 項集 | 支持度計數 |
| {L1} | 6 |
| {L2} | 7 |
| {L3} | 6 |
| {L4} | 2 |
| {L4} | 2 |
計算C2和L2
| C2 | |
| 項集 | 支持度計數 |
| {L1,L2} | 4 |
| {L1,L3} | 4 |
| {L1,L4} | 1 |
| {L1,L5} | 2 |
| {L2,L3} | 4 |
| {L2,L4} | 2 |
| {L2,L5} | 2 |
| {L3,L4} | 0 |
| {L3,L5} | 1 |
| {L4,L5} | 0 |
| L2:由C2剪枝得到L2 | |
| 項集 | 支持度計數 |
| {L1,L2} | 4 |
| {L1,L3} | 4 |
| {L1,L5} | 2 |
| {L2,L3} | 4 |
| {L2,L4} | 2 |
| {L2,L5} | 2 |
計算C3和L3
| C3:由L2計算三項集 | |
| {L1,L2}+{L1,L3} | {L1,L2,L3} |
| {L1,L2}+{L1,L5} | {L1,L2,L5} |
| {L1,L2}+{L2,L3} | {L1,L2,L3} |
| {L1,L2}+{L2,L4} | {L1,L2,L4} |
| {L1,L3}+{L1,L5} | {L1,L3,L5} |
| {L1,L3}+{L2,L3} | {L1,L2,L3} |
| {L1,L3}+{L2,L4} | 超過三項 |
| {L1,L3}+{L2,L5} | 超過三項 |
| {L1,L5}+{L2,L3} | 超過三項 |
| {L1,L5}+{L2,L4} | 超過三項 |
| {L1,L5}+{L2,L5} | {L1,L2,L5} |
| {L2,L3}+{L2,L4} | {L2,L3,L4} |
| {L2,L3}+{L2,L5} | {L2,L3,L5} |
| {L2,L4}+{L2,L5} | {L2,L4,L5} |
| L3:由C3剪枝得到L3 | |
| 項集 | 支持度計數 |
| {L1,L2,L3} | 3 |
| {L1,L2,L5} | 2 |
計算C4和L4
| C4:由L4計算四項集 | |
| {L1,L2,L3}+{L1,L2,L5} | {L1,L2,L3,L5} |
因為它的子集{L2,L3,L5}不是頻繁項集,此項集刪除,C4=0;
Apriori演算法優缺點:
優點:思路簡單;遞歸計算;實現方便
缺點:頻繁遍曆數據庫;生成候選集-----連接較多;占用空間大;運算量大。
2.FP-Growth演算法
頻繁模式樹增長演算法(Frequent Pattern Tree Growth)採用分而治之的 基本思想,將資料庫中的頻繁項集壓縮到一棵頻繁模式樹中,同時保持項集 之間的關聯關係。然後將這棵壓縮後的頻繁模式樹分成一些條件子樹,每個 條件子樹對應一個頻繁項,從而獲得頻繁項集,最後進行關聯規則挖掘。

FP-Growth演算法演示-------構造FP樹
事務資料庫的建立
| Tid | items |
| 1 | L1,L2,L5 |
| 2 | L2,L4 |
| 3 | L2,L3 |
| 4 | L1,L2,L4 |
| 5 | L1,L3 |
| 6 | L2,L3 |
| 7 | L1,L3 |
| 8 | L1,L2,L3,L5 |
| 9 | L1,L2,L3 |
掃描事務資料庫得到頻繁項目集F
| 從1到各點 | 各點路徑重覆次數 |
| 1-1 | 6 |
| 1-2 | 7 |
| 1-3 | 6 |
| 1-4 | 2 |
| 1-5 | 2 |
定義minsup=20%,即最小支持度為2,重新排列F
| 從1到各點 | 各點路徑重覆次數 |
| 1-2 | 7 |
| 1-1 | 6 |
| 1-3 | 6 |
| 1-4 | 2 |
| 1-5 | 2 |
重新調整事務資料庫
| Tid | items |
| 1 | L2,L1,L5 |
| 2 | L2,L4 |
| 3 | L2,L3 |
| 4 | L2,L1,L4 |
| 5 | L1,L3 |
| 6 | L2,L3 |
| 7 | L1,L3 |
| 8 | L2,L1,L3,L5 |
| 9 | L2,L1,L3 |
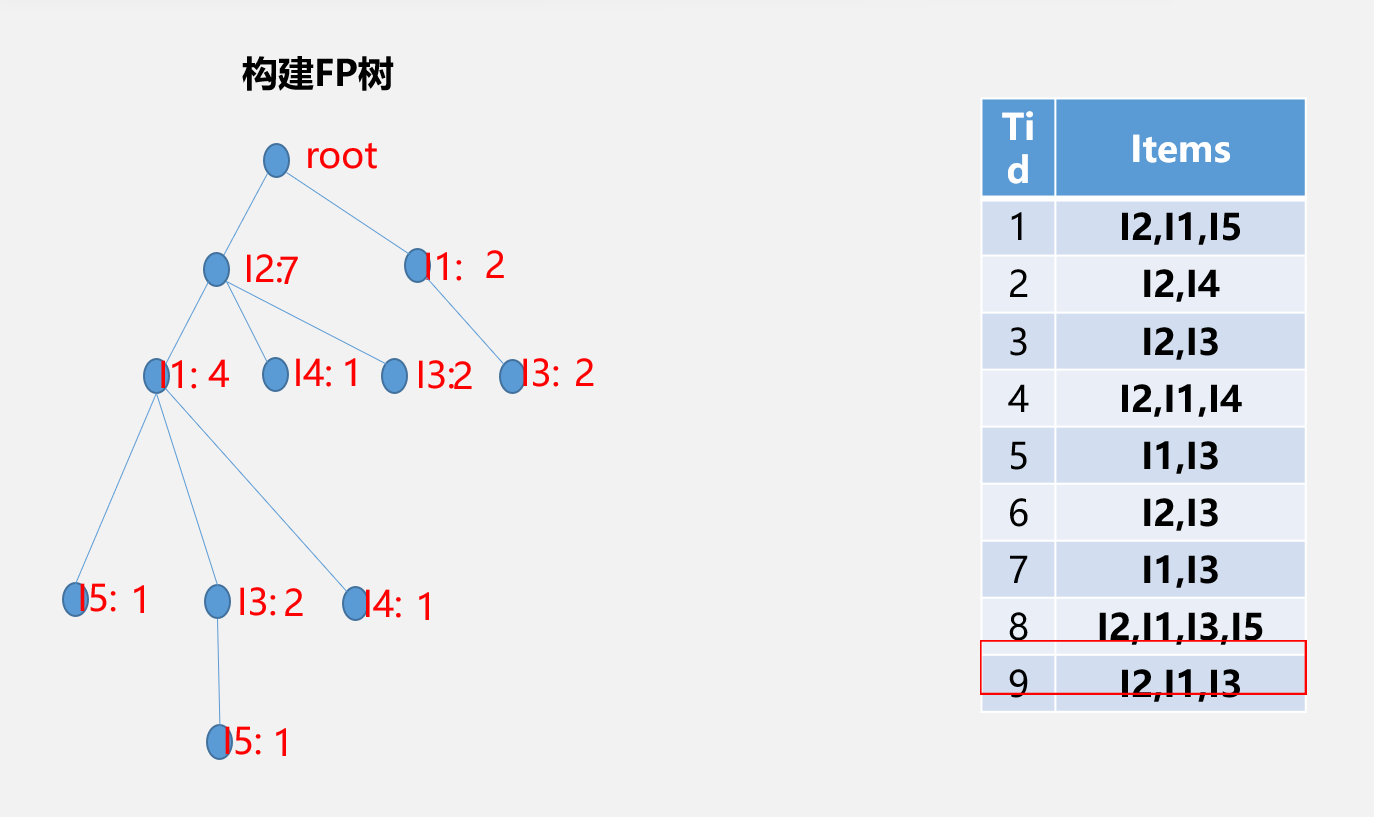
在FP樹中可以看到,從根節點到i5:1的路徑有兩條:
i2:7-->i1:4-->i5:1
i2:7-->i14-->i3:2-->i5:1
i2:7-->i1:4和i2:7-->i14-->i3:2因為最終到達的節點肯定是i5,所以將i5省略就是i5的條件模式基,記為{i2,i1:1}{i2,i1,i3:1}
條件模式基:{i2,i1:1}{i2,i1,i3:1}
因為i3:1x小於最小支持度2,所以講i3:1省略不計,i5的條件FP樹記為{i2:2,I1:2}
根據條件FP樹,我們可以進行全排列組合,得到挖掘出來的頻繁模式(這裡要將商品本 身,如i5也算進去,每個商品挖掘出來的頻繁模式必然包括這商品本身)
| 項 | 條件模式基 | 條件FP樹 | 產生頻繁模式 |
| I5 | {{I2 I1:1},{I2 I1 I3:1}} | {I2:2,I1:2} | {I2 I5:2},{I1 I5:2},{I2,I1:2} |
| I4 | {{I2 I1:1},{I2:1}} | {I2:2} | {I2 I4:2} |
| I3 | {{I2 I1:2},{I2:2},{I1:2}} | {I2:4,I1:2,I1:2} | {I2 I3:4},{I1 I3:4},{I2 I1 I3:2} |
| I1 | {{I1:4}} | {I2:4} | {I2 I1:4} |



