例7 級數求和 題目描述 已知: Sn =1+1/2+1/3+…+1/n。顯然對於任意一個整數 k,當 n 足夠大的時候,Sn>k。 現給出一個整數 k,要求計算出一個最小的 n,使得 Sn>k。 輸入格式 一個正整數 k 輸出格式 一個正整數 n 輸入樣例 1 輸出樣例 2 (1)編程思路。 用簡 ...
例7 級數求和
題目描述
已知: Sn =1+1/2+1/3+…+1/n。顯然對於任意一個整數 k,當 n 足夠大的時候,Sn>k。
現給出一個整數 k,要求計算出一個最小的 n,使得 Sn>k。
輸入格式
一個正整數 k
輸出格式
一個正整數 n
輸入樣例
1
輸出樣例
2
(1)編程思路。
用簡單的迴圈完成多項式求和。迴圈控制條件為和S<=K。
(2)源程式。
#include <stdio.h>
int main()
{
int k,n;
double s;
s=0;
n=0;
scanf("%d",&k);
do {
n++;
s+=1.0/n;
}while (s<=k);
printf("%d\n",n);
return 0;
}
習題7
7-1 Deck
本題選自北大POJ題庫 (http://poj.org/problem?id=1607)
Description
A single playing card can be placed on a table, carefully, so that the short edges of the card are parallel to the table's edge, and half the length of the card hangs over the edge of the table. If the card hung any further out, with its center of gravity off the table, it would fall off the table and flutter to the floor. The same reasoning applies if the card were placed on another card, rather than on a table.
Two playing cards can be arranged, carefully, with short edges parallel to table edges, to extend 3/4 of a card length beyond the edge of the table. The top card hangs half a card length past the edge of the bottom card. The bottom card hangs with only 1/4 of its length past the table's edge. The center of gravity of the two cards combined lies just over the edge of the table.
Three playing cards can be arranged, with short edges parallel to table edges, and each card touching at most one other card, to extend 11/12 of a card length beyond the edge of the table. The top two cards extend 3/4 of a card length beyond the edge of the bottom card, and the bottom card extends only 1/6 over the table's edge; the center of gravity of the three cards lines over the edges of the table.
If you keep stacking cards so that the edges are aligned and every card has at most one card above it and one below it, how far out can 4 cards extend over the table's edge? Or 52 cards? Or 1000 cards? Or 99999?
Input
Input contains several nonnegative integers, one to a line. No integer exceeds 99999.
Output
The standard output will contain, on successful completion of the program, a heading:
Cards Overhang
(that's two spaces between the words) and, following, a line for each input integer giving the length of the longest overhang achievable with the given number of cards, measured in cardlengths, and rounded to the nearest thousandth. The length must be expressed with at least one digit before the decimal point and exactly three digits after it. The number of cards is right-justified in column 5, and the decimal points for the lengths lie in column 12.
Sample Input
1
2
30
Sample Output
Cards Overhang
1 0.500
2 0.750
30 1.997
(1)編程思路。
本題題意為:將紙牌沿桌子推出,第1張推出桌面1/2,第2張推出第1張1/4,第3張1/6,依次類推。求n張紙牌推出桌面的長度。
即輸入正整數n,求S=1/2+1/4+…+1/(2n)的值。
簡單迴圈處理即可。
(2)源程式。
#include <stdio.h>
int main()
{
int n,i;
double s;
printf("Cards Overhang\n");
while (scanf("%d",&n)!=EOF)
{
s=0;
for (i=1;i<=n;i++)
s+=1.0/(2*i);
printf("%5d %8.3lf\n",n,s);
}
return 0;
}
7-2 求π的值
題目描述
根據公式
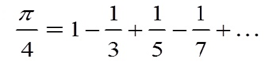
計算π的值,要求精確到最後一項的絕對值小於10–4。
輸入格式
無
輸出格式
求得的π的值。
(1)編程思路。
若計算如下多項式

用一個簡單迴圈即可實現。
int n=1;
double p=0.0;
while (1.0/n>=0.0001)
{
p=p+1.0/n;
n+=2;
}
但現在是加1項然後減1項交替進行,如何解決?
一個最簡單的辦法是用一個變數flag作為符號標誌,初始時f=1,運算p=p+1.0*f/n=p+1.0/n;完成加項運算;之後 f=-f,f值為-1,運算p=p+1.0*f/n=p-1.0/n;完成減項運算;再之後 f=-f,f值為1,…。這樣,通過f的值在1,-1之間切換從而完成加項與減項的交替進行。
(2)源程式。
#include <stdio.h>
int main()
{
int n=1,f=1;
double p=0.0;
while (1.0/n>=0.0001)
{
p=p+1.0*f/n;
f=-f;
n+=2;
}
printf("%f\n",4*p);
return 0;
}
7-3 u Calculate e
本題選自北大POJ題庫 (http://poj.org/problem?id=1517)
Description
A simple mathematical formula for e is
e=Σ0<=i<=n1/i!
where n is allowed to go to infinity. This can actually yield very accurate approximations of e using relatively small values of n.
Input
No input
Output
Output the approximations of e generated by the above formula for the values of n from 0 to 9. The beginning of your output should appear similar to that shown below.
Sample Input
no input
Sample Output
n e
- -----------
0 1
1 2
2 2.5
3 2.666666667
4 2.708333333
...
(1)編程思路。
題目要求根據公式e=1+1/1!+1/2!+…+1/n!求e的值。可以用一個簡單迴圈完成計算。設初始時,e=1.0,p=1,迴圈程式編寫如下:
for (i=1;i<=n;i++)
{
p=p*i;
e=e+1.0/p;
}
註意:不要寫成二重迴圈
for (e=1.0, i=1;i<=n;i++)
{
for (p=1,j=1;j<=i;j++) // 迴圈求 i! 的值
p=p*i;
e=e+1.0/p;
}
因為,i!=i*(i-1)!,這樣求i!時可以利用前一次求得的(i-1)!,無需每次重新求取。
(2)源程式。
#include <stdio.h>
int main()
{
int i,p;
double e;
printf("n e\n");
printf("- -----------\n");
printf("0 1\n");
e=1.0;
p=1;
for (i=1;i<=9;i++)
{
p=p*i;
e=e+1.0/p;
if (i==1) printf("%d %.0f\n",i,e);
else if (i==2) printf("%d %.1f\n",i,e);
else printf("%d %.9f\n",i,e);
}
return 0;
}



