堆排序演算法

排序---堆排序

一：定義

作為選擇排序的改進版，堆排序可以把每一趟元素的比較結果保存下來，以便我們在選擇最小/大元素時對已經比較過的元素做出相應的調整。

二：堆排序演算法

作為選擇排序的改進版，堆排序可以把每一趟元素的比較結果保存下來，以便我們在選擇最小/大元素時對已經比較過的元素做出相應的調整。

堆排序是一種樹形選擇排序，在排序過程中可以把元素看成是一顆完全二叉樹，每個節點都大（小）於它的兩個子節點，當每個節點都大於等於它的兩個子節點時，就稱為大頂堆，也叫堆有序； 當每個節點都小於等於它的兩個子節點時，就稱為小頂堆。

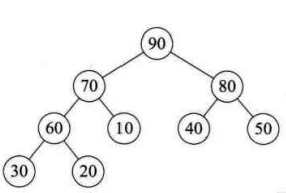
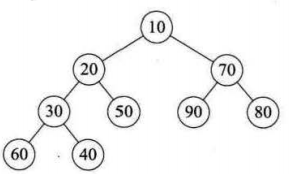
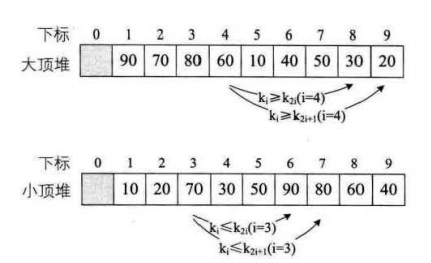
下麵是我們要保存在數組中的堆的形式

二：堆排序演算法

1.將長度為n的待排序的數組進行堆有序化構造成一個大頂堆
 
2.將根節點與尾節點交換並輸出此時的尾節點
 
3.將剩餘的n -1個節點重新進行堆有序化
 
4.重覆步驟2，步驟3直至構造成一個有序序列

三：圖解演示，構造堆（大頂堆）

{5, 2, 6, 0, 3, 9, 1, 7, 4, 8}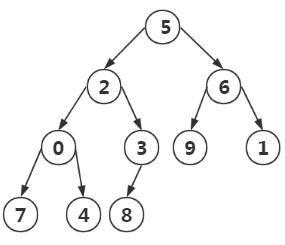

在構造有序堆時，我們開始只需要掃描一半的元素（n/2-1 ~ 0）即可，為什麼?

因為(n/2-1)~0的節點才有子節點，如圖1，n=8,(n/2-1) = 3 即3 2 1 0這個四個節點才有子節點

第一次找到[n/2]處，進行構造：

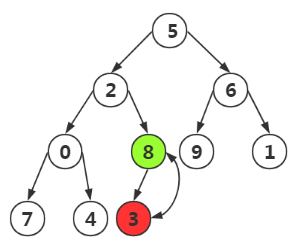
我們比較父節點，左右孩子結點的大小，將最大的作為堆頂

第二次，我們對上次找到位置-1即可，找到結點0，對其左右孩子比較，構造這三個結點的最大堆

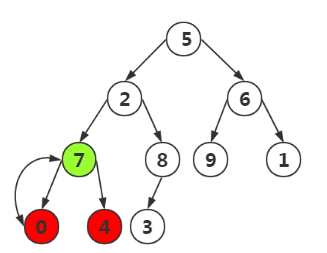
第三次，我們找到結點6，要對其進行構造，結果如下

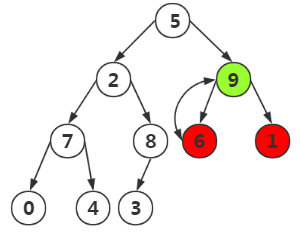
第四次（重點），我們不止要構造雙親和左右孩子，我們還要比較其孩子結點為根的堆是否正確，不然我們需要進行調整

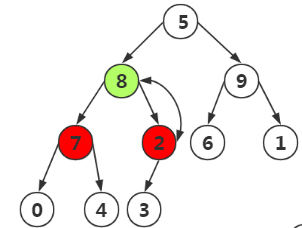
我們發現將8,7,2三個結點變為了最大堆，但是其中2,3子樹不再是一個最大堆，我們需要對其修改

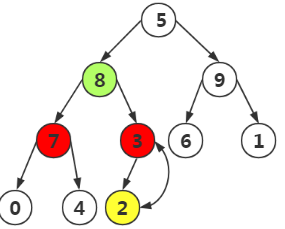
第五次：選取結點9進行構造

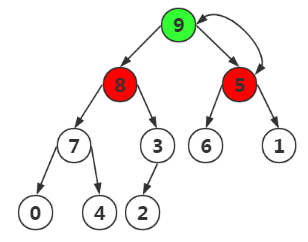
發現以結點5為根的子樹不是最大堆，我們需要進行調整

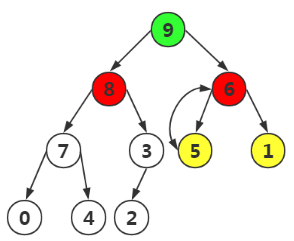
完成最大堆的構建

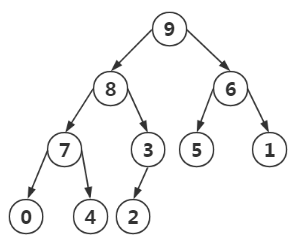
四：圖解演示：堆排序（堆存儲在數組中）

第一步：將最大值和最後的一個元素交換

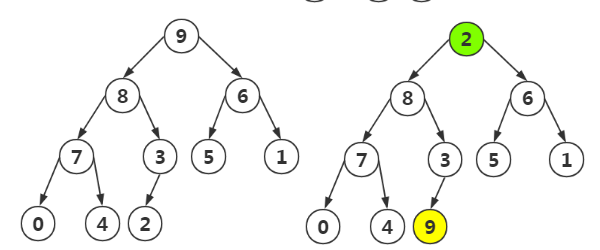
第二步：將剩餘的結點再次進行堆構造

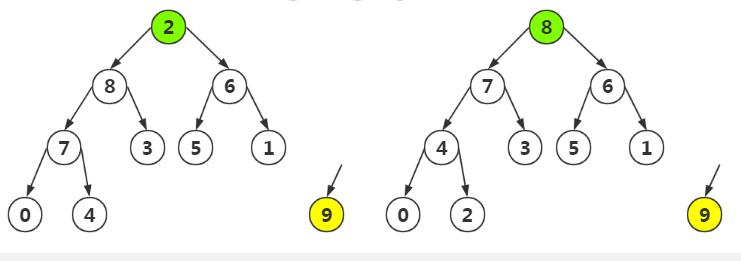
第三步：參照第一步

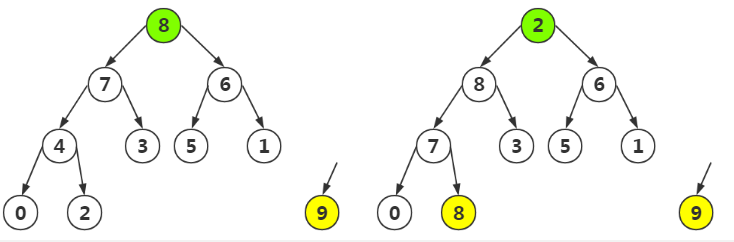
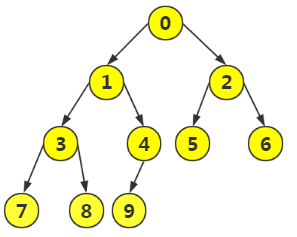
按照上面迴圈，最終結果為

五：代碼實現

void swap(int K[], int i, int j)
{
    int temp = K[i];
    K[i] = K[j];
    K[j] = temp;
}

//大頂堆的構造，傳入的i是父節點
void HeapAdjust(int k[],int p,int n)
{
    int i,temp;
    temp = k[p];
    for (i = 2 * p; i <= n;i*=2)    //逐漸去找左右孩子結點
    {
        //找到兩個孩子結點中最大的
        if (i < n&&k[i] < k[i + 1])
            i++;
        //父節點和孩子最大的進行判斷，調整，變為最大堆
        if (temp >= k[i])
            break;
        //將父節點數據變為最大的，將原來的數據還是放在temp中，
        k[p] = k[i];    //若是孩子結點的數據更大，我們會將數據上移，為他插入的點提供位置
        p = i;
    }
    //當我們在for迴圈中找到了p子樹中，滿足條件的點，我們就加入數據到該點p,註意：p點原來數據已經被上移動了
    //若沒有找到，就是相當於對其值不變
    //插入
    k[p] = temp;
}

//大頂堆排序
void HeapSort(int k[], int n)
{
    int i;
    //首先將無序數列轉換為大頂堆
    for (i = n / 2; i > 0;i--)    //註意由於是完全二叉樹，所以我們從一半向前構造，傳入父節點
        HeapAdjust(k, i, n);

    //上面大頂堆已經構造完成，我們現在需要排序，每次將最大的元素放入最後
    //然後將剩餘元素重新構造大頂堆，將最大元素放在剩餘最後
    for (i = n; i >1;i--)
    {
        swap(k, 1, i);
        HeapAdjust(k, 1, i - 1);
    }
}


int main()
{
    int i;
    int a[11] = {-1, 5, 2, 6, 0, 3, 9, 1, 7, 4, 8 };
    HeapSort(a, 10);

    for (i = 1; i <= 10; i++)
        printf("%d ", a[i]);

    system("pause");
    return 0;
}

六：性能分析

運行時間主要消耗在構造堆和重建堆時的反覆篩選上。
構造堆的時間複雜度為O(n)
重建堆時時間複雜度為O(nlogn)。
所以總體就是O(nlogn)。
不適合排序序列個數較少的情況