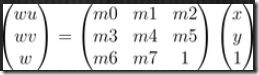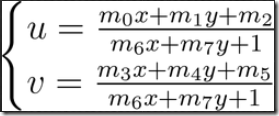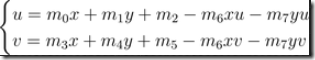轉自 http://www.hanyeah.com/blog/post/%E5%9B%9B%E9%A1%B6%E7%82%B9%E6%A0%A1%E6%AD%A3%E9%80%8F%E8%A7%86%E5%8F%98%E6%8D%A2%E7%9A%84%E7%BA%BF%E6%80%A7%E6%96... ...
設計給了兩張圖,一張俯視圖A,一張側視圖B,要把A上的點映射到B上,B上的點映射到A上。怎麼做?
只有兩張圖
我們可以通過工具,獲取每張圖4個頂點的坐標,坐標之間必然存在映射關係,Pa = f(Pb),用矩陣表示,Pa = m*Pa。我們要求m。m用3*3的矩陣。
參考:https://www.cnblogs.com/faith0217/articles/5027490.html
透視變換(Perspective Transformation)用於解決仿射變換(Affine Transformation)無法改變形狀內部的相對位置關係的問題。類似Photoshop中的“自由變換”功能,或者GIMP中的“透視”功能,都可以用透視變換矩陣來實現。
現在給定2個四邊形:Poly1={{x1, y1}, {x2, y2}, {x3, y3}, {x4, y4}}、Poly2={{u1, v1}, {u2, v2}, {u3, v3}, {u4, v4}},求做一個透視變換Matrix,滿足Poly1的點能夠變形(Warp)到Poly2中的點。
透視變換矩陣的形式為:
顯然,我們需要求解的只是矩陣中8個未知量;已知量包括四邊形的4個頂點 x 2個坐標(x, y),一共是8個方程,數量剛剛好。對於每個頂點坐標,Poly1中的點總是通過下麵的方程轉換到Poly2中:
問題的關鍵在於,上面的公式需要求解非線性方程。因此,在解決Homography的問題上,常常用最小二乘法(Least Squares)求得參數估計。
其實稍加分析就不難發現,上面那個使用了分式的所謂“非線性方程”,實際上可以變形為:
它居然變成了線性方程!看來一切試圖用Newton迭代的演算法都是沒有必要的,因為我們可以用最簡單的線性代數來解決:
下麵是我用matlab計算的代碼,mat就是我們要求的矩陣,順便把mat的逆矩陣mat2也求出來,逆變換也有了。
沒有matlab也沒關係,運算不難,矩陣運算的庫也不難找。
u1 = 0; v1 = 0; u2 = 1000; v2 = 0; u3 = 1000; v3 = 1000; u4 = 0; v4 = 1000; x1 = -375; y1 = 510; x2 = 254; y2 = 152; x3 = 1134; y3 = 304; x4 = 782; y4 = 828; a = [ x1, y1, 1, 0, 0, 0, -x1*u1, -y1*u1; 0, 0, 0, x1, y1, 1, -x1*v1, -y1*v1; x2, y2, 1, 0, 0, 0, -x2*u2, -y2*u2; 0, 0, 0, x2, y2, 1, -x2*v2, -y2*v2; x3, y3, 1, 0, 0, 0, -x3*u3, -y3*u3; 0, 0, 0, x3, y3, 1, -x3*v3, -y3*v3; x4, y4, 1, 0, 0, 0, -x4*u4, -y4*u4; 0, 0, 0, x4, y4, 1, -x4*v4, -y4*v4 ]; u = [u1,v1,u2,v2,u3,v3,u4,v4]'; m = a\u; mat = [m(1),m(2),m(3);m(4),m(5),m(6);m(7),m(8),1]; mat2 = inv(mat);
最後求出來結果是
mat =
0.622681800333835 -2.26554353140329 1388.93287614087
1.22602742955981 2.15410964579083 -638.835633268398
1.38327614714492e-06 0.00133144792441439 1
mat2 =
0.434597104229077 0.59516884730679 -223.411138468529
-0.177460145184904 0.0897866610409582 303.8391483172
0.000235677774164818 -0.000120369546353085 0.595763035916078可以用mat*[x1,y1,1]來驗證結果的正確性。
-------------------------------------------------------------------------------------
C#求解方法(應用Math.NET庫)
-------------------------------------------------------------------------------------
double u1 = pEnvelope.MinX; double v1 = pEnvelope.MinY; double u2 = pEnvelope.MaxX; double v2 = pEnvelope.MinY; double u3 = pEnvelope.MaxX; double v3 = pEnvelope.MaxY; double u4 = pEnvelope.MinX; double v4 = pEnvelope.MaxY; double x1 = results[0][0]; double y1 = results[0][1]; double x2 = results[1][0]; double y2 = results[1][1]; double x3 = results[2][0]; double y3 = results[2][1]; double x4 = results[3][0]; double y4 = results[3][1]; // double[,] x = { { x1, y1, 1, 0, 0, 0, -x1*u1, -y1*u1 }, { 0, 0, 0, x1, y1, 1, -x1 * v1, -y1 * v1}, { x2, y2, 1, 0, 0, 0, -x2 * u2, -y2 * u2}, { 0, 0, 0, x2, y2, 1, -x2 * v2, -y2 * v2}, { x3, y3, 1, 0, 0, 0, -x3 * u3, -y3 * u3}, { 0, 0, 0, x3, y3, 1, -x3 * v3, -y3 * v3}, { x4, y4, 1, 0, 0, 0, -x4 * u4, -y4 * u4}, { 0, 0, 0, x4, y4, 1, -x4 * v4, -y4 * v4} }; var matrixX = DenseMatrix.OfArray(x); var vectorB = new DenseVector(new[] { u1, v1, u2, v2, u3, v3, u4, v4 }); var resultX = new DenseVector(8); matrixX.GramSchmidt().Solve(vectorB, resultX); //驗證 //Console.WriteLine(x1 + ", " + y1 + ", " + x2 + ", " + y2 + ", " + x3 + ", " + y3 + ", " + x4 + ", " + y4); //Console.WriteLine(u1 + ", " + v1 + ", " + u2 + ", " + v2 + ", " + u3 + ", " + v3 + ", " + u4 + ", " + v4); //Console.WriteLine(resultX); //var u = (resultX[0] * x1 + resultX[1] * y1 + resultX[2]) / (resultX[6] * x1 + resultX[7] * y1 + 1); //Console.WriteLine(u1 + " " + u); double[] result = new double[] { resultX[0], resultX[1], resultX[2], resultX[3], resultX[4], resultX[5], resultX[6], resultX[7], 1 };