樹-二叉樹的基本概念

二叉樹的特點

• 每個結點至多有二棵子樹(即不存在度大於2的結點)
• 二叉樹的子樹有左、右之分，且其次序不能任意顛倒

卡特蘭數

具有n個結點的不同形態的二叉樹數目，即所謂的n階卡特蘭數。（也是含有n個結點的棧的出隊順序的總情況）

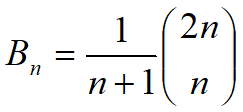
二叉樹的性質（約定空二叉樹的高度為-1）

• 高度為h>=0的二叉樹至少有h+1個結點。
• 高度為h>=0的二叉樹至多有2^h+1-1個結點
• 含有n>=1個結點的二叉樹的高度至多為n-1
• 含有n>=1個結點的二叉樹的高度至少為[log₂n](向下取整)
• 對於任何一棵二叉樹，如果其葉節點的數目為n₀，度為2的結點數目為n₂,則n₀=n₂+1

證明：設n₁為二叉樹中度為1的結點數目，故結點總數為n=n₀+n₁+n₂.

　　　在二叉樹中，除根結點外，每個結點都有一條分支進入，設B為分支總數，則n=B+1.

　　　又因為分支有度為1和度為2的結點射出，B=n₁+2n₂

　　　於是n=n₁+2n₂+1=n₀+n₁+n₂，得到n₀=n₂+1

滿二叉樹

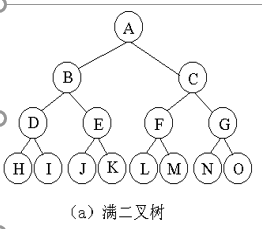
•  定義：一棵高度為h且有2^h+1-1個結點的二叉樹稱為滿二叉樹

完全二叉樹

• 定義：若一棵二叉樹最多只有最下麵的2層上結點的度數可以小於2，並且最下麵一層上的節點都集中在該層的最左邊，則這種二叉樹稱為近似滿二叉樹
• 性質：如果對一棵有n個結點的完全二叉樹的結點按層序編號，則對任一結點i(1<=i<=n)，有

  　　　　(1)  如果i=1，則結點i是二叉樹的根，無雙親；如果i>1，則其雙親是[i/2]（向下取整）

 　　　　 (2)  如果2i>n，則結點i無左孩子；如果2i<=n，則其左孩子是2i

  　　　　(3)  如果2i+1>n，則結點i無右孩子；如果2i+1<=n，則其右孩子是2i+1

• 例題：一棵完全二叉樹有1001個結點，其中葉節點的個數是（501）

　　　　解：最後一個分支結點的序號為[1001/2]=500,故葉子節點的個數為501