每天兩題02

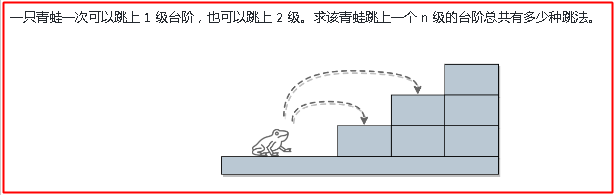
題目一：

 思路：當n=1的時候很明顯只有一種跳法；

　　   當n>1的時候，那麼總共的跳法應該就是第一次跳一級臺階還剩下n-1個臺階、第一次跳兩級臺階還剩下n-2個臺階，這兩種情況的總和，而至於這裡的n-1和n-2個臺階，同理可以繼續拆分，是不是覺得很熟悉，還是斐波那契數列，這裡用的還是分治的思想，代碼跟上一篇一樣，不過還是寫一下（省略最外層的類名，其實用遞歸是最容易的。。。。）：

public static int jump(int n){
        if (n == 1) {
            return 1;
        }
        if (n==2) {
            return 2;
        }
        int prepre=1;
        int pre=2;
        int current=0;
        for (int i = 2; i < n; i++) {
            current = prepre+pre;
            prepre = pre;
            pre = current;
        }
        return current;
        
    }
    public static void main(String[] args) {
        System.out.println(jump(4));//5
        
    }

 　　莫名感覺這種問題好有趣啊，哈哈哈

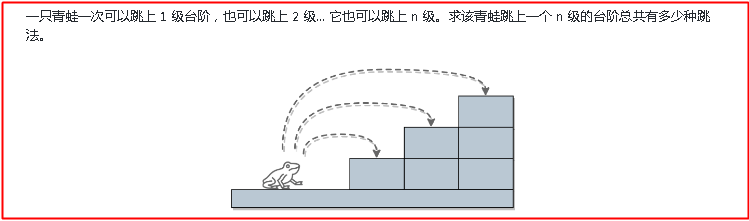
題目二：這個是題目一的強化版

 　　先用遞歸試試：假設只有一個臺階的跳法為f（1），有兩個臺階的跳法為f(2)，三個臺階的跳法為f（3）。。。。

　　先試試n=5的時候，總共的跳法分為幾種情況：第一次跳一個，那麼還有4個臺階，這四個臺階的跳法為f(4);   如果第一次跳兩個，剩下3個臺階，跳法為f(3),依次類推，還有f(2),f(1)，那麼f(5)=f(4)+f(3)+f(2)+f(1)，到這裡其實問題已經很明瞭了，那麼f（n）==f(n-1)+f(n-2)+...+f(2)+f(1)，再寫一個f（n-1）==f(n-2)+f(n-3)+...+f(2)+f(1)，將這兩個等式減一下就可以得到f（n）=2f（n-1）

　　那麼代碼表示為：

public static int jump(int n){
        if(n==1){
            return 1;
        }
        return 2*jump(n-1);
    }
    
    public static void main(String[] args) {
        System.out.println(jump(3));//4
        
    }

　　第二種方式：我們還是假設n=5，那麼青蛙不管怎麼樣第五級臺階時肯定要跳到的，至於前面四個臺階，每一個臺階都不確定，要麼跳到要麼沒有跳到，那麼可能性就是2x2x2x2=16種可能，即2^4

可以很輕易的推出n級臺階總共的可能性為：2^（n-1），這種的話代碼也就沒什麼好說的了

　　第三種：動態規劃，動態規劃也就是將計算的中間的狀態給保存起來，避免下一次還要進行重覆的計算，缺點很明顯就是需要一定的記憶體空間

　　這種方法簡單的說就是：假設有3個臺階，我只需要計算到第1個臺階的所有可能性，到第二個臺階的所有可能性，然後相加就是到第三個臺階的所有可能性；這裡很有點不好理解，其實可以這樣想，已經確定第一個臺階跳到第三個臺階和第二個臺階跳到第三個臺階這兩種分類，那麼我們只需要考慮青蛙從地上跳到第一個臺階的所有可能和跳到第二個臺階的所有可能，然後加起來就ok了，這裡我們用一個數組存儲中間狀態：

public static int jump(int n){
        int[] arr = new int[n];
        //將數組arr每個位置都填充1
        Arrays.fill(arr, 1);
        //外層的這個for迴圈就是分別計算第一個臺階、第二個臺階...第n個臺階的所有跳法
        for (int i = 1; i < n; i++)
            //這個for迴圈的作用：比如計算第三個臺階，那麼就需要將第一個臺階所有跳法加上第二個臺階所有跳法
            for (int j = 0; j < i; j++)
                arr[i] += arr[j];
        return arr[n - 1];
    }
    
    
    public static void main(String[] args) {
        System.out.println(jump(8));//128
        
    }