一、概念介紹 素數又稱為質數。一個大於1的自然數(從2開始),除了1和它本身外,不能被其他自然數整除的叫做素數,否則稱為合數。 0和1既不是素數也不是合數,最小的素數是2。 二、代碼 方法一: 註意:在for迴圈判斷時不能忘記 i <= sqrt(num) 的等號,因為假設 p*p = n , n的 ...
一、概念介紹
素數又稱為質數。一個大於1的自然數(從2開始),除了1和它本身外,不能被其他自然數整除的叫做素數,否則稱為合數。
0和1既不是素數也不是合數,最小的素數是2。
二、代碼
方法一:
bool is_Prime(int num){
int i;
for(i = 2;i <= sqrt(num);i++){
if(num % i == 0)//一旦發現有因數,則返回false
return false;
}
return true;
}
註意:在for迴圈判斷時不能忘記 i <= sqrt(num) 的等號,因為假設 p*p = n , n的因數是可以取到 sqrt(n) 的,如判斷 9 是不是素數,如果沒有等號會出現 9是素數,而實際上 9不是素數。
方法二:
關於質數分佈的規律:大於等於5的質數一定和6的倍數相鄰。例如5和7,11和13,17和19等等;
證明:令x≥1,將大於等於5的自然數表示如下:
··· 6x-1,6x,6x+1,6x+2,6x+3,6x+4,6x+5,6(x+1),6(x+1)+1 ···
可以看到,不和6的倍數相鄰的數為6x+2,6x+3,6x+4,由於2(3x+1),3(2x+1),2(3x+2),所以它們一定不是素數,再除去6x本身,顯然,素數要出現只可能出現在6x的相鄰兩側。因此在5到sqrt(n)中每6個數只判斷2個,時間複雜度O(sqrt(n)/3)。
在高配版和尊享版中,都是一個剪枝的思想,高配版中裁剪了不必要的偶數,尊享版中裁剪了不和6的倍數相鄰的數,雖然都沒有降低時間複雜度的階數,但都一定程度上加快了判斷的速度。
原文鏈接:https://blog.csdn.net/songyunli1111/article/details/78690447
/*一種高效的方法*/ bool isPrime_3(int num){ //兩個較小數另外處理 if(num == 2 || num == 3) return true; //不在6的倍數兩側的一定不是質數 if(num % 6 != 1 && num % 6 != 5) return false; int i; //在6的倍數兩側的也可能不是質數 for(i = 2;i <= sqrt(num);i += 6){ if(num % i == 0 || num % (i + 2) == 0) return false; } //排除所有,剩餘的是質數 return true; }
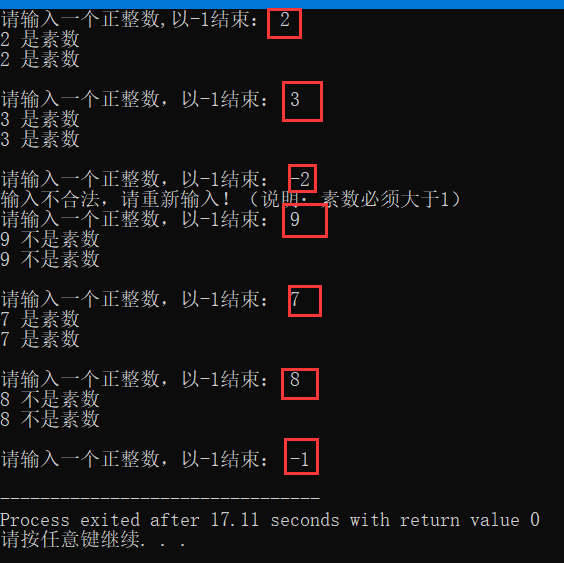
三、測試
對負數與0,1進行異常處理
int main(){
int num;
bool result1,result2;
printf("請輸入一個正整數,以-1結束: ");
scanf("%d",&num);
while(num < 2 && num != -1){
printf("輸入不合法,請重新輸入!(說明:素數必須大於1)\n");
printf("請輸入一個正整數,以-1結束: ");
scanf("%d",&num);
}
while(num >= 2 && num != -1){
result1 = isPrime(num);
result2 = isPrime_3(num);
if(result1 == true)
printf("%d 是素數\n",num);
else if(result1 == false)
printf("%d 不是素數\n",num);
if(result2 == true)
printf("%d 是素數\n\n",num);
else if(result2 == false)
printf("%d 不是素數\n\n",num);
printf("請輸入一個正整數,以-1結束: ");
scanf("%d",&num);
while(num < 2 && num != -1){
printf("輸入不合法,請重新輸入!(說明:素數必須大於1)\n");
printf("請輸入一個正整數,以-1結束: ");
scanf("%d",&num);
}
}
}
四、截圖